物理（発展）と物理基礎の解説を当日解いてかきました

今年もセンター物理と物理基礎について、丁寧にわかりやすく解説をする企画を実施しました。２０１８年の大学入試センター試験が実施されるのはセンター試験２日目の１月１４日（日）です。そこで１４日（日）の２１時ころから解き初めて解説を行いました。なおこの企画は２０１２年からはじめていますが、新課程になっての過去三年分はこちらを参考にしてください。

2017物理　2017物理基礎
2016物理　2016物理基礎
2015物理　2015物理基礎

昨年から、より丁寧に詳しくを優先させて、図や絵を手書きではなくPCで描き、数式等もできるだけ省かずに解説しています。また今まで撮りためてきたYoutube等の実験動画も関連する問題につけることにしました。

一人で行っており、図・絵を含め、更新はすべてが手作業ですので、多少わかりにくさいところがあるかもしれません。ご了承ください。ご連絡いただければ改定を加えていきます。

メニュー

・センター物理（発展）の出題問題を予想！　平成30年1月11日

・センターに変わる新入試「大学入学共通テスト」プレテストを解く！　平成30年1月9日

物理（発展）の解説

※　物理基礎の解説はページの下にありますが、長いのでここをクリックしてください

東進のサイトにセンター試験２０１８の問題が公開されたので解きはじめます。（平成30年1月14日午後8時57分）

※　誤りのある可能性があります。使用にはご注意ください。また何かございましたらご連絡いただければと思います。確認後訂正いたします。

第１問（必答問題）

問１

２つの物体の衝突の問題ですね。衝突後の運動エネルギーを求めるためには、衝突後の速さが必要になります。運動量の保存から衝突後の速さをもとめて、その後に一体となった物体の運動エネルギーを求めましょう。

衝突後の速さをVとすると、運動量の保存から、

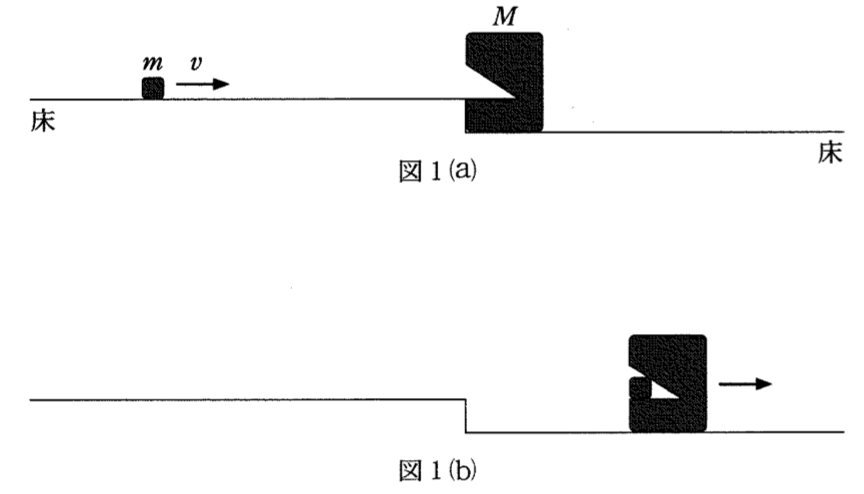
mv + M×0 = mV + MV

（衝突前の運動量の和＝衝突後の運動量の和）
※　右向きを正としました

となります。これをVについて解くと、

よって衝突後の一体となった物体の運動エネルギーを求めると、

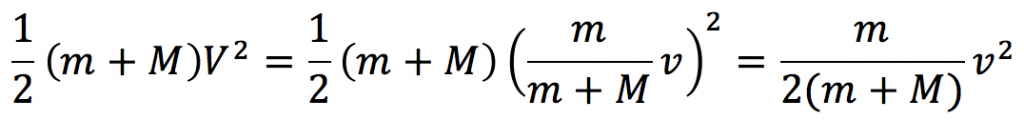
となります。答えは⑤番です。

質問が届きました

問2

①　音の速さVは、331.5+0.6t（ｔは気温）で、気温に比例して速くなります。不正解です。

②　１オクターブあがると、その音の振動数の二倍の振動数になります。波長が２倍になるわけではないので、不正解です。オクターブまで知っている生徒が少ないのかもしれません。ちょっと嫌な問題ですよね。

③　回折とは音の回り込む現象のことをいいます。教室の窓を少しあけておくと外の騒音が教室中に聞こえるのも回折によります。正解です。

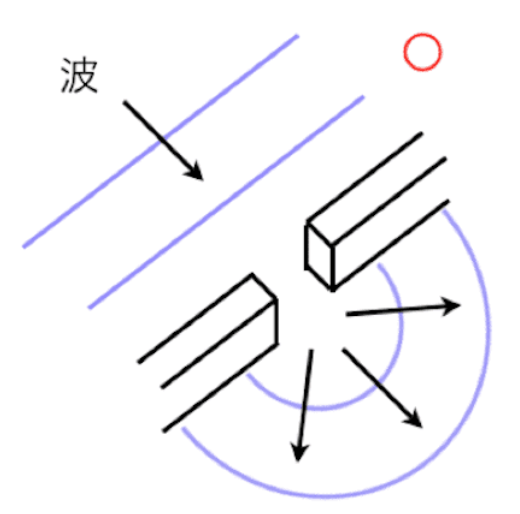
波の回折の例

④　振動数が等しくて、振幅が異なる２つの波が重なっても「うなり」は生じません。「うなり」は振動数が少し異なる場合に発生します。不正解です。

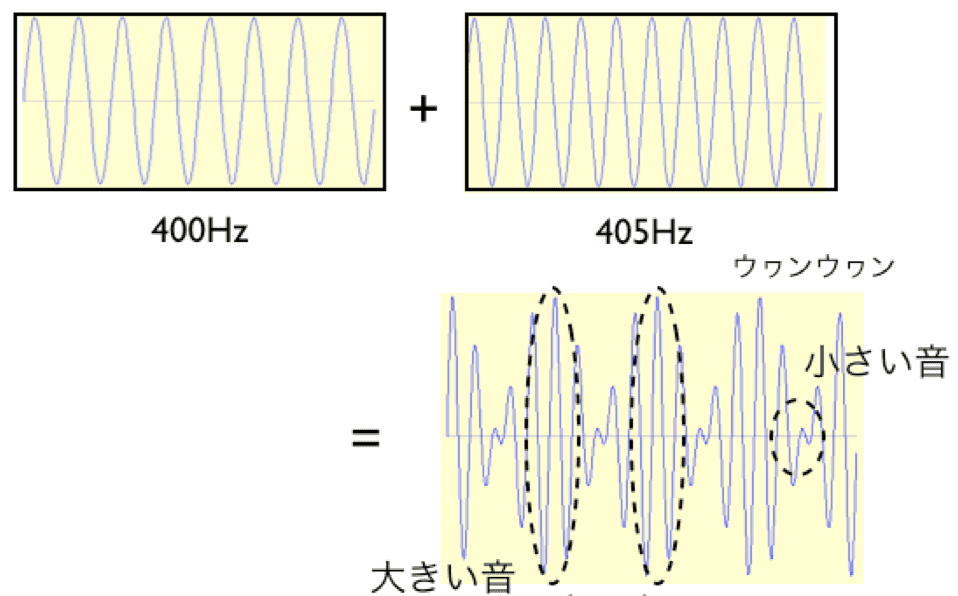
うなりの例（物理基礎２０１８で詳しく出題されました（下記参照））

なお、うなりの様子はこちらを御覧ください。

＜うなりの様子＞

⑤　ドップラー効果の問題ですね。音源が観測者に近づく速さが大きいと、波長が短くなり、音は高く聞こえます。つまり振動数は大きくなります。不正解です。

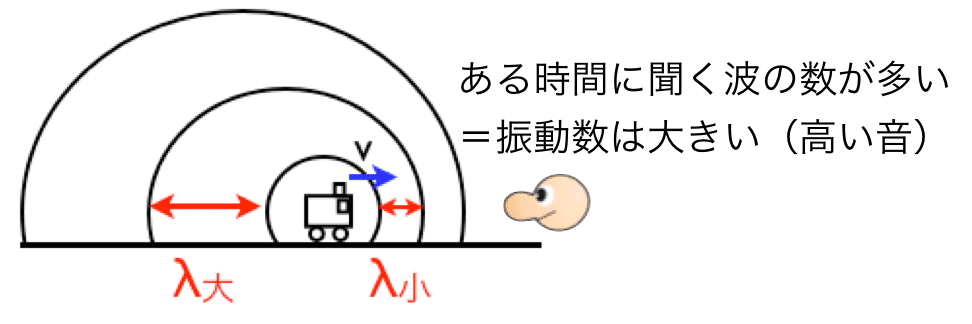
　音源が動くと、その前方では波長が短くになります。

参考

短い動画ですが、動きがわかると思います。

スマホでも簡単にドップラー効果を観察することができます。こちらはスマホを回転テーブルに乗せたときの様子です。回転テーブルがなくても、スマホを手に持って前後にすばやく動かすと観察ができます。振動数は高めの１０００Hzくらいが良いかと思います。

問３

P点に＋１C（単位電荷）を置いて、静電気力を引いてみましょう（電場とは単位電荷にはたらく力）。プラスやマイナスの、斥力や引力に注意して、引いていきましょう。

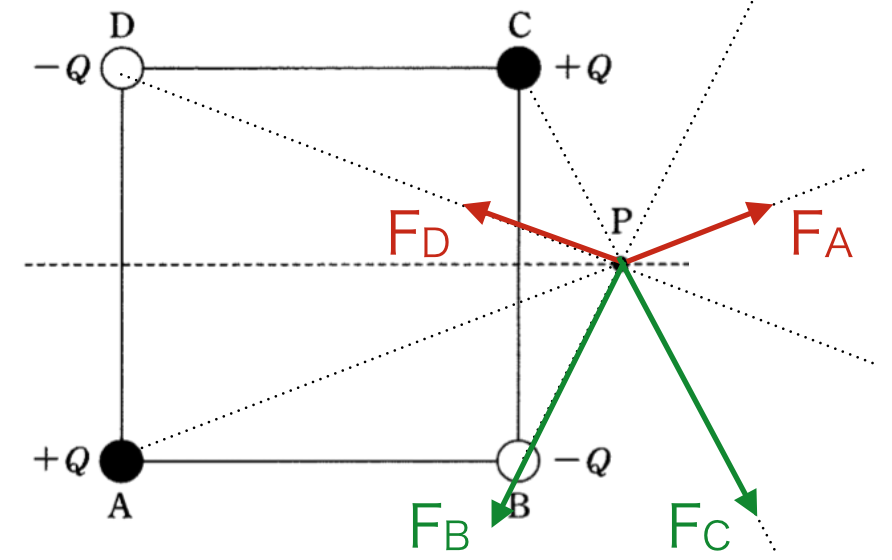
なおAとD（赤）またCやB（緑）はPからの距離が等距離なので同じ色にしました。またA・D（赤）はC・B（緑）に比べて遠いので矢印の長さは短くなっています。

AとD、BとCのベクトルを合成すると、次の図のようになります。

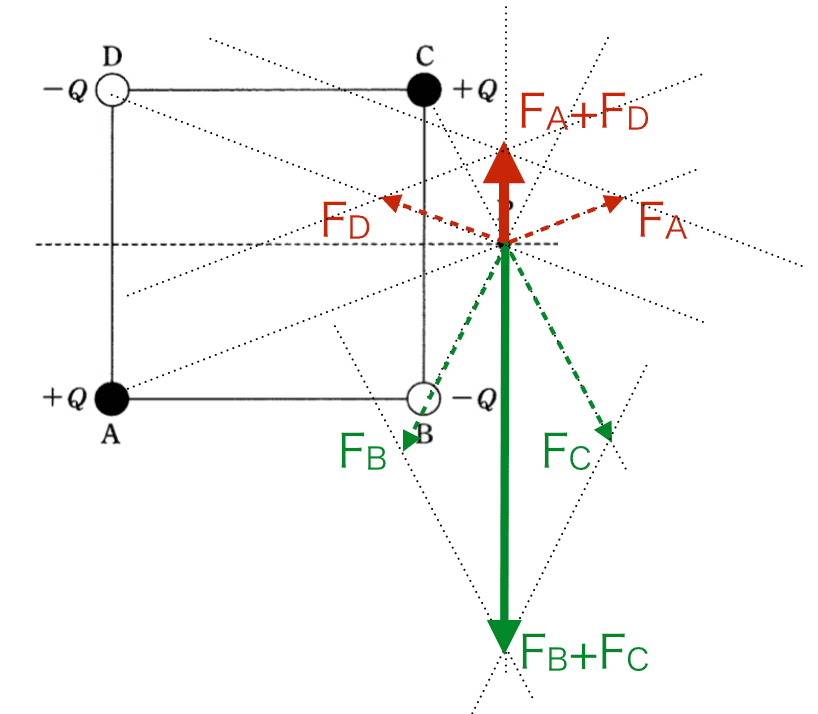
最後にA・D，B・Cのベクトルを合成すると、

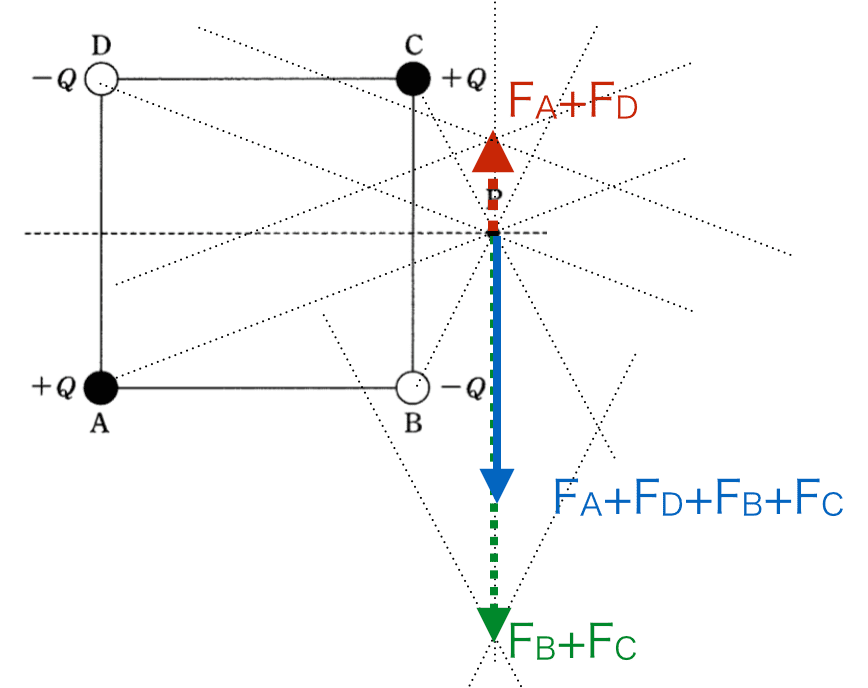
となります。正解は⑦番ですね。

参考

ちょっとわかりにくいかもしれませんが、３Dで電位を描くと次のようになります。電位の傾きが電場を示します。Pの位置をみると、手前が低くなっており、手前のほうに転がりそうな様子がわかりますでしょうか。

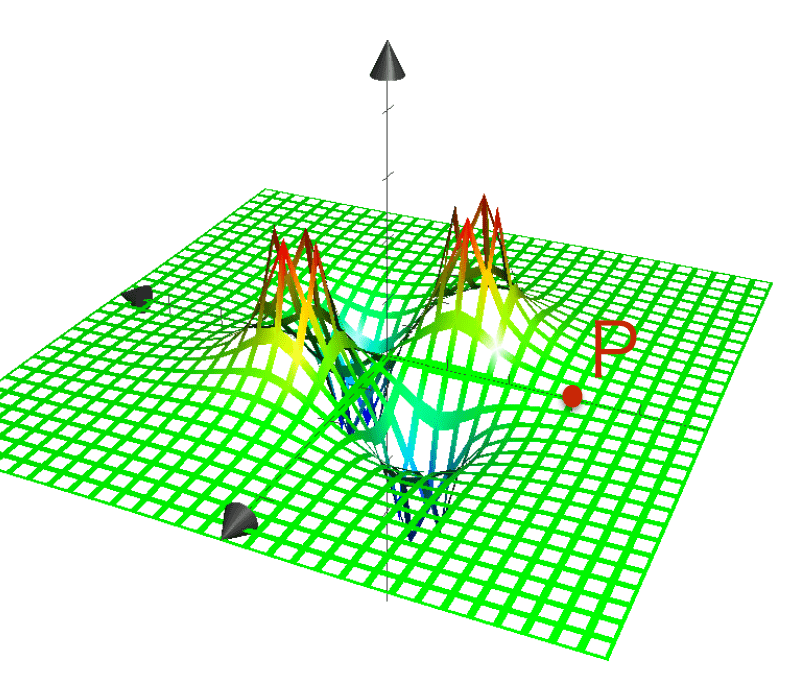
※　この３Dグラフは、Grapherを使って描きました。

問４

気体分子の平均の運動エネルギーは、

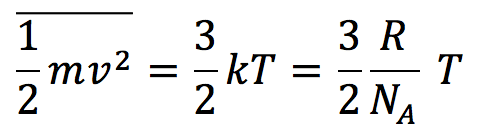
となります（ｋはボルツマン定数、Rは気体定数、N_Aはアボガドロ数）。そのため絶対温度に比例しますが、分子量Mとは関係がありません。

また上の式より、２乗平均速度は、

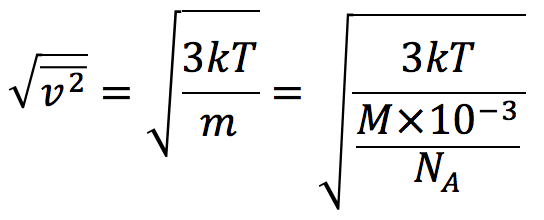
となり、分子量Mと反比例の関係にあります。ヘリウム（4.0）のほうがネオン（20.18）より分子量Mは小さいので、ヘリウムのほうが２乗平均速度は速いということになります。答えは①番です。

感想

予想通り分子運動論が出ましたね。公式を覚えていない人でも、分子運動論の手順に沿っていけば答えにたどり着けますが、時間の関係から厳しいかもしれません。センターとしては、

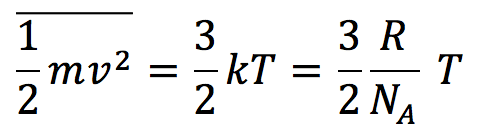
は覚えておくということでしょうか。

問５

これは定番のような重心問題で、一度解いたことのある生徒は解けたと思います（ひねりのきいた問題？なので、初見だと厳しいと思います）。まず大きな円（半径３ｃｍ）の重心は０です。

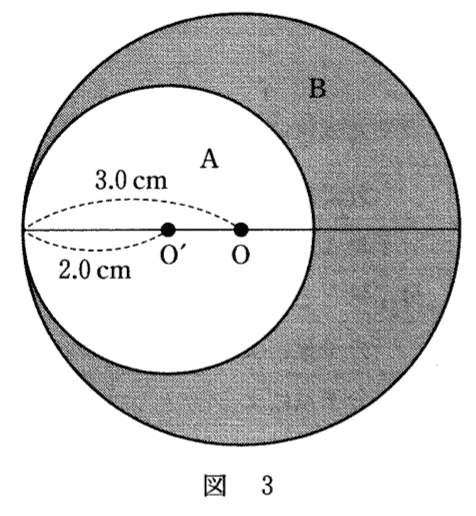
そしてくり抜いた円A（半径２ｃｍ）の重心はO’です。あとで重さを使うために、Aの面積を求めておくとπ2²=4π[cm²]となります。三日月型Bの重心の位置を適当にOから右側ｘ[cm]の位置にあるとします。Bの面積を求めておくと、π3²−π2²=5π[cm²]となります。

この三日月型のBのかけた部分にくり抜いた円のAをもう一度入れると、重心は０に戻りますね。このことから０のまわりの力のモーメントのつり合いより、

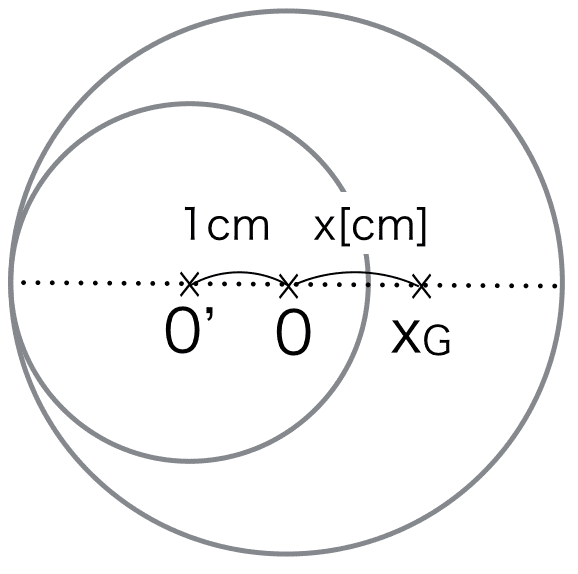
1　×（4πρ）＝　x　×（5πρ）

※　なお厚さが一様なので、重さは面積に比例すると考え、適当な文字ρをつけて単位を「N」にして使っています。

　となります。これを解くと、ｘ＝0.8[cm]となり、適当に置いたｘが正で出てきたので、右側0.8[cm]、②番が答えとなります。

第１問の感想

なかなか歯ごたえのある難しい問題であったように思います。問４・問５などは教科書でも細かい部分になっており、一度目を通しておかないと解けないような問題だったかもしれませｎ。満点をとれた受験生は少ないのではないでしょうか。

第２問　A

問１

コンデンサーに電荷が蓄えられていない状態から、スイッチをいれたので答えは①番のグラフになりますね。

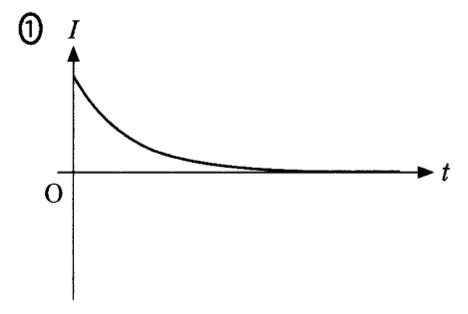
はじめは電荷が０なのでどんどん電荷がたまりますが、しばらくすると電荷がもうコンデンサーに入った状態になり、極板に静電気力の斥力が発生してい、電荷が入りにくくなっていき、十分時間がたつとコンデンサーには電荷が入ることができなくなり、電流は０となります。これでコンデンサーの充電が完了した状態です。

参考

・コンデンサーの充電の様子がよくわかる動画を撮影しました。

・微積で考えてみるコーナーも以前に作っているので、もしよろしければこちらからどうぞ。

問２

十分に時間が経過すると、コンデンサーには電圧V[V]がすべてかかります。抵抗には電流が流れなくなるため、電圧降下はなくなり、電圧は０[V]となります。

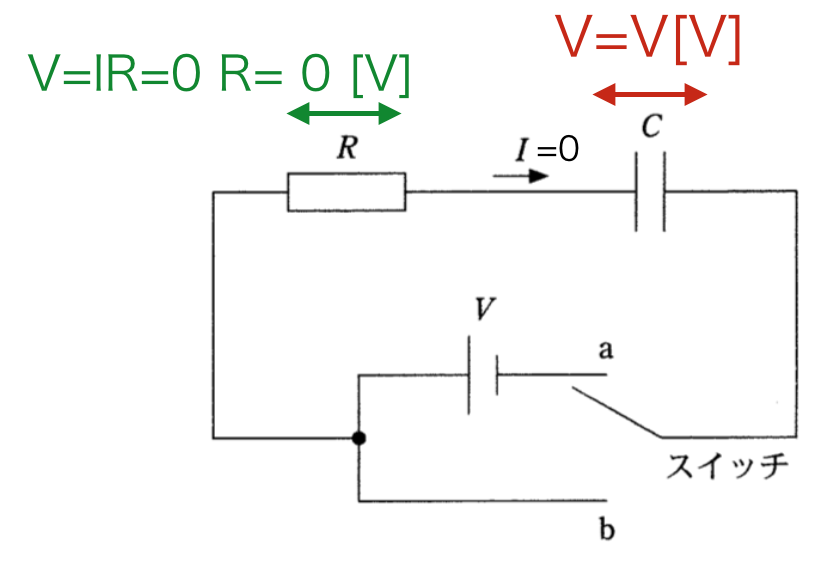
このときにコンデンサーに蓄えられた電気量は、

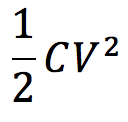
です。スイッチをｂに倒すと、蓄えられた電荷がすべて放出されるので、コンデンサーのエネルギーがすべて抵抗でのジュール熱となります。よって答えは⑧番です。

第２問　B

問３

ファラデーの電磁誘導の法則では、誘導起電力は、

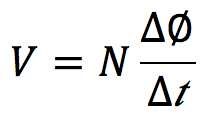
という式で表されて、コイルの中を貫く磁束の時間変化によって誘導起電力が発生することがわかります。

今回の問題では、磁束密度Bの中にコイルが入ると、このコイルがすべて入るまでは一定の速さで落下をしたということが書かれているので、磁束の時間変化も一定、つまり誘導起電力は一定であることがわかります。

そして、コイルが磁場中に完全に入ると磁束が変化しないため、電磁誘導が起こらなくなり誘導起電力が０になります。

コイルの抵抗値はRで一定なので、流れる電流も誘導起電力（電圧）に合わせて変化するので、③または④に絞ることができます。

最後に向きについてですが、向きとして問題文ではabcdaが正となっていますが、それを踏まえて右手で考えてみると、今回の回路には次の図のように電流が流れます。紙面裏から表向きの磁場があるので、それを打ち消す向き、つまり親指を紙面表から裏向きに向けると、電流が時計回りに流れるのがわかりますね。

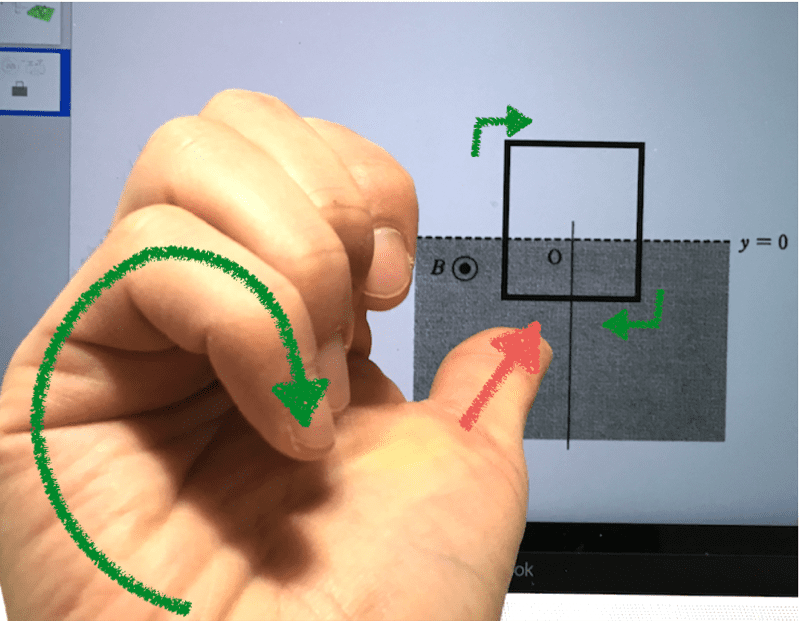
※　右手出やりましょう！緑が電流の流れを示します。

　緑の回転方向をみると、adcbaとなっているので、負の領域になっている④番を選びましょう。

問４

「コイルが一定の速度で落下をした」ということは、重力と電流が磁場から受ける力がつり合っているということがわかりますね（運動方程式より）。よって力のつり合いの式を作ってみましょう。

電流が磁場から受ける力の向きはフレミング左手の法則よりｙ軸正の向き。

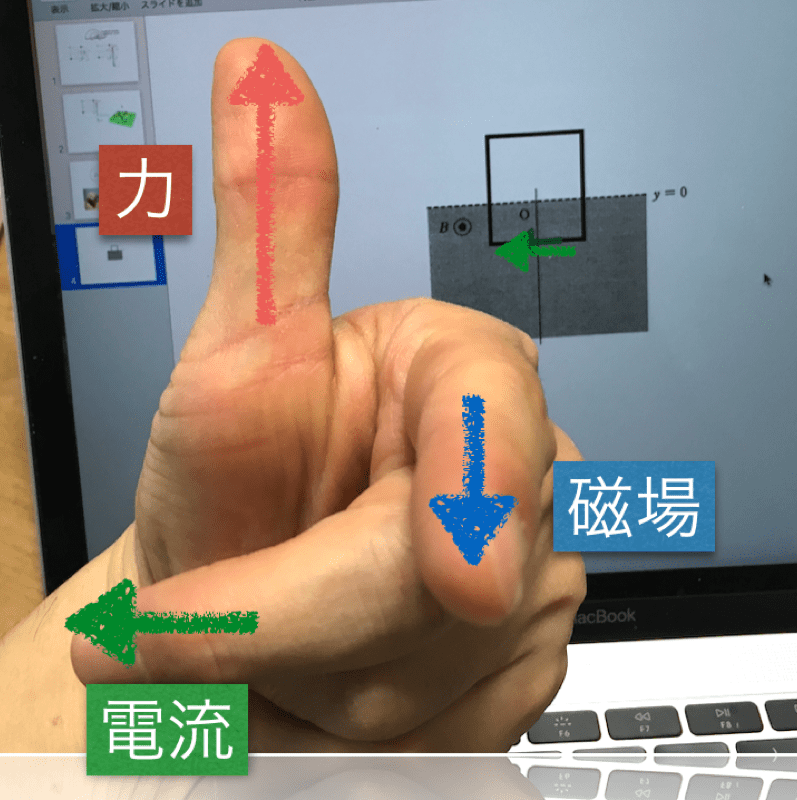
※　左手を使ってやってみましょう。

　これが重力のｍｇとつりあっているはずです。

この電流が磁場から受ける力の大きさを求めましょう。公式F=LIBより、F=wIBとなります。ここで、自分で置いた電流Iを求めます。

まず誘導起電力Vの大きさは、abの棒の部分からV=BLv=Bwvとなります。また抵抗値はRはなので、コイルに流れる電流Iは

　となります。よって電流が磁場から受ける力Fは、

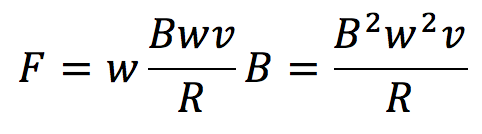
　となります。

これをつかって、コイルにはたらく力のつり合いをたてると、

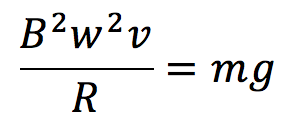
上向きの力＝下向きの力

　となります。これをｖについて解くと、

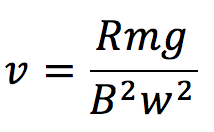
となります。答えは④番ですね。

第２問の感想

予想どおり、Aにてコンデンサーと抵抗の回路の問題が出てきました。難しくはない一般的な問題ですね。またコの字型回路がでると予想をしたのですが、そちらの予想ははずれてしまい、コイルでの電磁誘導を問うという問題でした。さほど難しい問題ではなかったと思います。

第３問 A

問１

波の式に関する問題ですね。まず原点（ｘ＝０）の媒質は時刻０のときにA[m]の場所にいるために、時間とともに下がってくるしか無いので、ｙ‐ｔグラフは次のようなcos型を描きます。

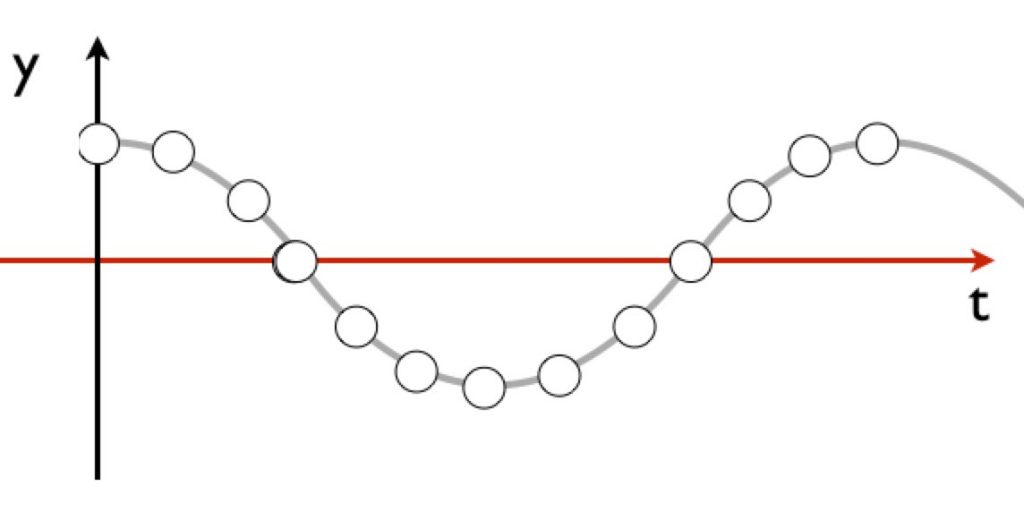
よって、このように表すことができます。

y=Acosωt

この式の形を変形させていくと

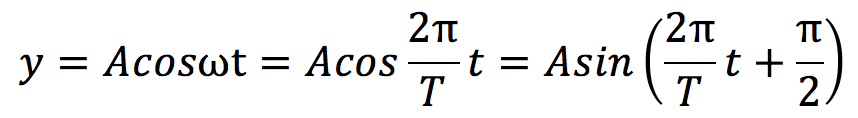
となり、(a)に入るものはπ/2となります。また周期Tについては、t=0秒からt=0.1秒で0.1ｍから0mまで落ちてきたので、その４倍の0.4秒となります。

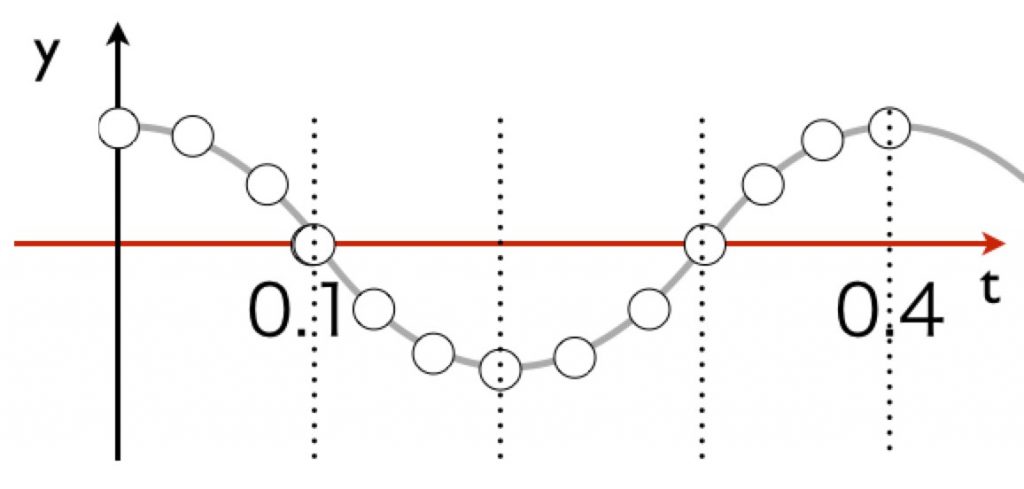
答えは⑥番です。

問２

入射波と反射波を合成してみましょう。次の図の赤線が合成波です。節の位置は常に振幅が０になっている場所なので、‐0.2～0.2の範囲では、−0.1と0.1の場所となります。

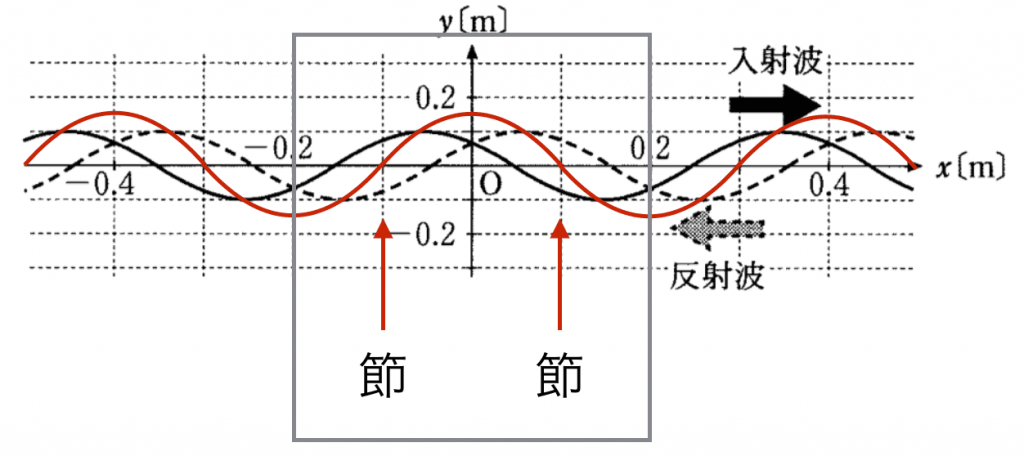
また今回は問われていませんが、腹の位置はその間である−0.2、０、0.2となります。腹と腹、節と節の間隔は波長（λ＝0.4m）の半分なので、0.2mごとに現れます。よって反射する場所である１ｍの位置では、0.2ごとに見ていくと、

腹　０、0.2、0.4、0.6、0.8、1.0

節　0.1、0.3、0.5、0.7、0.9、1.1

　腹の位置になっていることがわかりますね。反射面の変位が０になるのが固定されている固定端反射で、反射面がバタバタと大きく振動する腹になっているのが自由端反射です。よって答えは②番となります。

参考

自由端反射の様子はこちらを御覧ください。反射するときに媒質が大きく動くこと・位相が変化しないことがわかりますね。

問3

あまり見慣れない問題だと思います。まずは基本振動については、3T/8と同じ状態に戻ってくるので、（a）を選びます。

　次に２倍振動についてはパターンをみると、次はT/8と同じ状態であることがわかり、（ｃ）を選びぶことができます。

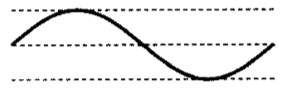
最後に合成波ですが、上の２つを合成するので、

重ねて、みると左側の振幅が小さく、右側の負の振幅が大きくなる

↓

合成

　このような形になることが考えられます。3T/8の左右反転パターンとなりますね。よって、（e）を選びます。答えは①番です。

参考

こちらは弦の振動の実験の様子です。今回のような振動のパターンが見えると思います。

実際の弦の振動の様子を観察すると、今回の問題のように様々な振動パターンが入っています。例えばギターのある音を分析してみたら次のような結果になりました。

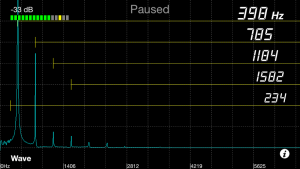
基本振動が398Hz、その２倍、３倍振動も入っていることがわかりますね。

第３問　B

問４

疎から密の反射では、位相が反転しますので、[ウ]はπ（パイ）ずれるということになります。間隔がｄのとき、経路差は２倍の２ｄとなります。

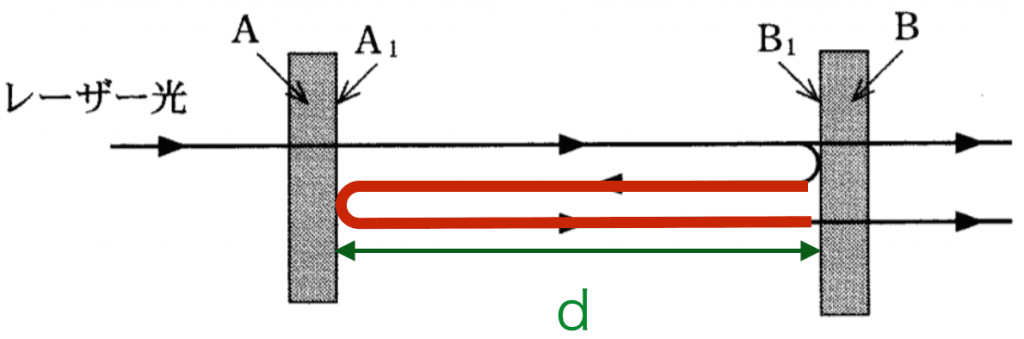
このときに強めあったということから、

強め合い：2d=mλ（ｍは整数）

という式になっていることがわかりますね（２回反射がありますが、どちらも疎から密の反射であり、位相がπずれています。あわせるともとに戻るので、強めあいの条件は変わりません）。間隔をd+λ/2にすると、経路さは同様に２倍の、2d＋λとなります。これは

2d+λ=mλ＋λ=（ｍ＋１）λ（ｍは整数）

となりますので、強め合いの条件に合致します。また徐々に変化させるときに、ｍλとｍλ＋λの間には、ｍλ＋1/2λのときがあるので、はじめ強め合い（ｍλ）、そして弱め合い（ｍλ＋1/2λ）、ふたたび強め合い（ｍλ＋λ）というようになります。答えは４番ですね。

問５

強め合いの条件式より

2d＝ｍλ　式A

また波の式ｃ＝ｆλより、

ｆ＝ｃ／λ　式B

となります。式A・Bより、

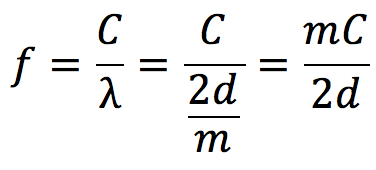
となります。答えは③番ですね。

また振動数をｆからｆ＋Δｆにしたときに一度弱めあったのちにまた強めあったということから、ｆ＋Δｆのときにmからｍ＋１の強め合いに変わったということがわかります。

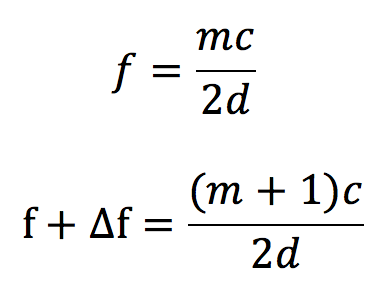
このことから、２つの式の差をとると、

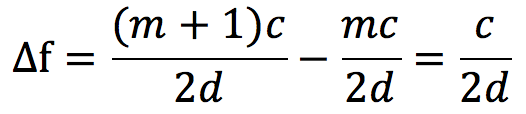
ｃとｄに数値を代入すると、1.5×10⁹となります。答えは⑥番ですね。

第３問の感想

波動の問題ですが、波の式が出てきたので戸惑った生徒もいたかもしれません。ただ第１問を落としたとしても、その他の問題が難しくなかったので、落ち着いて先に進めれば問題はないですね。

追記　この問題、d=0.10mというのがひっかかります。実際にこのような大きな幅で干渉が観察できるようなレベルで起こるのでしょうか。ちょっと疑問に思っています。

第４問　A

問１

静かに手を離したときに、その場で静止している位置の最大値なので、摩擦力が最大（静止）摩擦力になっていることがわかりますね。

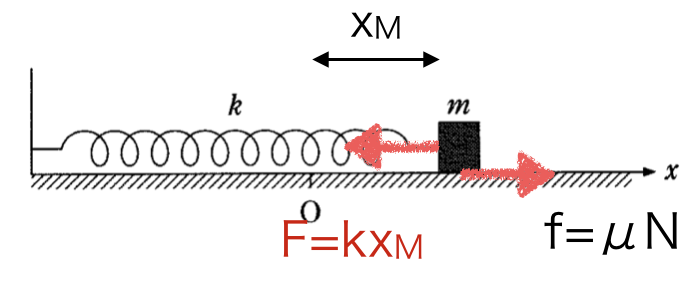
力のつり合いから、

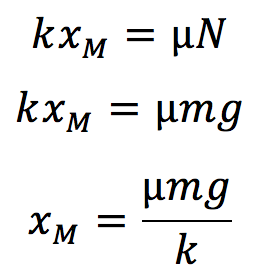
となります。答えは②番です。

問２

ア

小物体にはたらく力は、動摩擦力とばねの力の２種類があります。ｘが正のときの状態を考えると次の図のようになるので、

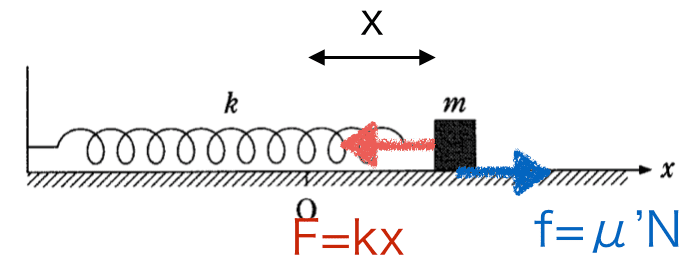
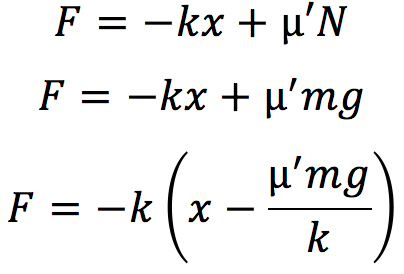
このようになります。

イ

時間t₁は再び速度が０になるときの時刻であるので、単振動の周期Tの半分であるということがわかりますね。周期Tを求めると、周期の公式より

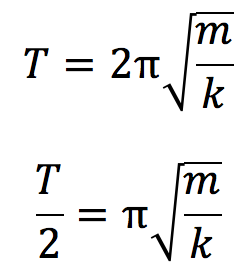
となります。これらの結果から⑤番が正解です。

第４問　B

問３

ピストンのまわりの力のつり合いから、

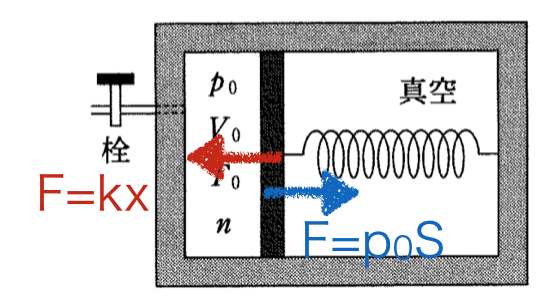
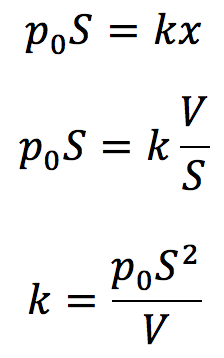
となります（ここでV=Sxを利用しました）。またばねのエネルギーはその公式に代入すると、

となります。また状態方程式(PV=nRT）より、

となります。よって答えは④番です。

問４

単原子分子理想気体の内部エネルギーUは、

と表すことができます。温度がT₀からTまで増加したので、単原子分子の内部エネルギーの変化量ΔUは 、

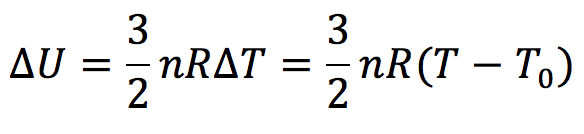
となります。答えは⑨番ですね。

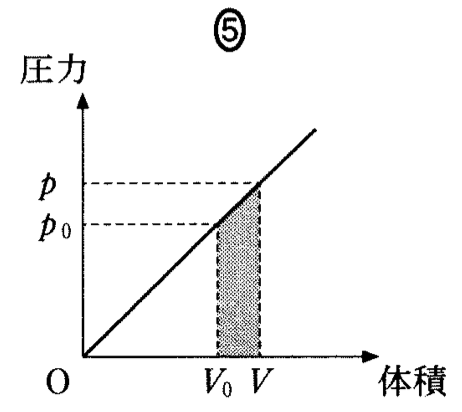
問５

P-V図の囲んだ面積は仕事に相当するので、答えは⑤番です。

感想

単振動も、熱力学第一法則の問題も、基本的でやさしい問題でした。

第５問（選択）

問１

ケプラーの第二法則（面積速度一定の法則）より

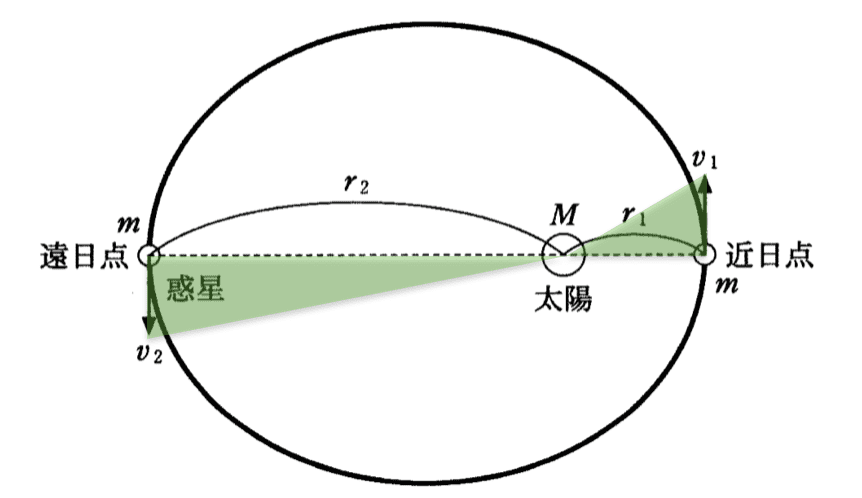
となります。答えは⑥番ですね。

問２

面積速度一定の法則から、近日点では速度が最大になり、また遠日点では速度が最小となります。運動エネルギーは速度の２乗に比例するので、(a)のグラフを選ぶことができます。

また万有引力の位置エネルギーは無限遠を0[J]とすると、

と表すことができます。よって、dを選ぶことができます。答えは③番です。

問３

ア

万有引力が向心力となる円運動の運動方程式から、

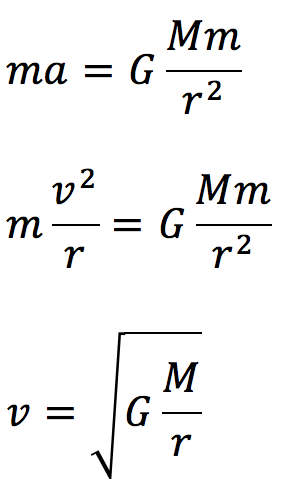
となります。また近日点で円運動と同じエネルギーしかなかった場合には、より位置エネルギーの大きな遠日点に到達することができません。このように円軌道から楕円軌道にうつるためにはより大きなエネルギーが必要です。よってイは「大きい」を選びます。なおエネルギーが大き過ぎるとだ円起動からはずれて、放物線の軌道になります。

答えは⑦番です。

感想

予想をしたとおり、万有引力に関する問題が出題されました。ただし難しくはなく基本的な問題でした。

第６問（選択）

問１

①　クーロン力（静電気力）によって結びついていないので不正解です。

②　質量欠損に関するものですね。ばらばらの状態のほうがエネルギーが大きく、くっつくとエネルギーが小さくなります。このくっついているためのエネルギーが結合エネルギーΔEであり、くっついている方が質量Δｍがわずかに小さくなっています（ΔE=Δm c²）。これは正解ですね。

③　クォークは素粒子の一つであるので、電子やニュートリノが内部で結びついているわけではありません。不正解です。

④　クォークは電荷をもっています。不正解です。

⑤　自然界に存在する基本的な力は４つあり、重力・電磁気力・弱い力・強い力です。３つではないので不正解です。

問２

α崩壊ではヘリウムが飛び出すので、質量数が−４、原子番号が−２されます。またβ崩壊では、中性子が陽子に変化するので、原子番号のみ１増えます。質量数はα崩壊しか減らないので、まずは質量数から決めていきましょう。

Uは２３８、Pbは２０６なので、その差は３２（２３８‐２０６）です。よってα崩壊が３２÷４＝８回おこったことがわかります。８回起こると、Uの原子番号は、

９２−２×８＝７６

となります。Pbの原子番号は８２なので、β崩壊は８２−７６＝６回おこればいいことになります。答えは⑨番ですね。

問３

サイコロを振ったときに取り除かれる原子核に数は全体の６分の１になりますので、残る数は６分の５となります。よってはじめの数1000から

１回目　１０００×5/6

２回目　１０００×5/6×5/6　＝　１０００×5/6の２乗

３回目　１０００×5/6×5/6×5/6　＝　１０００×5/6の３乗

ｎ回目の個数Nは、

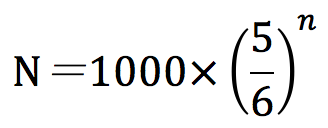
となりますね。よってグラフはｃを選びます。一応ですがパソコンでグラフを描いてみました。

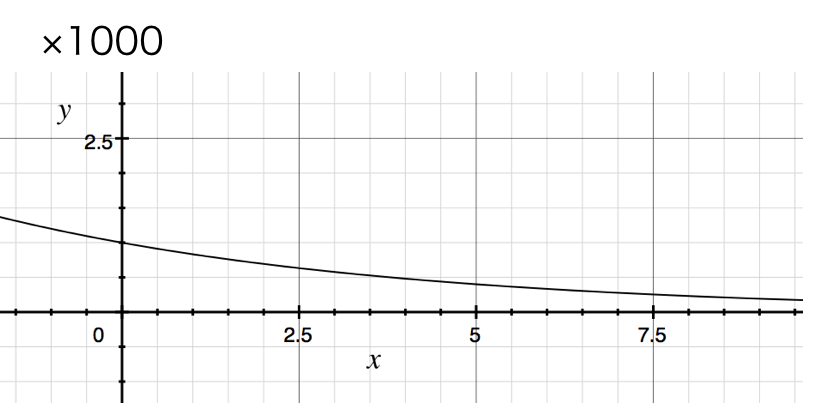
また半減期をTとするので、２Tの時間が立つとさらに半分になりますから、500の半分で250ということになります。答えは⑦番ですね。

第６問の感想

予想したとおり、半減期に関する問題が出題されましたね。ただ対策をとってこなくても、解けるような簡単な問題でした。

全体の感想

今回のセンター試験は今までと比べて三日月型の重心問題が出てきたり、波の式が出てきたり、分子運動論が出てきたり、と細かいというか、あまり見慣れない問題も多かったのかもしれません。またオクターブなど教養的な知識が必要になったものもあります。

個人的な意見ですが、例年よりも少し難しかったのではないかと思いますが、実際平均点はどのような感じで出るのでしょうか。

私の予想した問題も結構でたので、ブログを読んでくれた方や、学校で対面で伝えた生徒の皆さんはあまり面食らわずに落ち着いてできたのではないかと思っております。

高校３年生の皆さんは自己採点したら、不足していた知識は復習をして、結果は気にせずに個別入試にむけて進んで下さい。

物理基礎の解説

第１問

問１

ゆっくりと持ち上げていることから、物体の運動エネルギーは増えてないと読みとります。位置エネルギーのみ変化したので、はじめの場所を位置エネルギーの基準とすると、

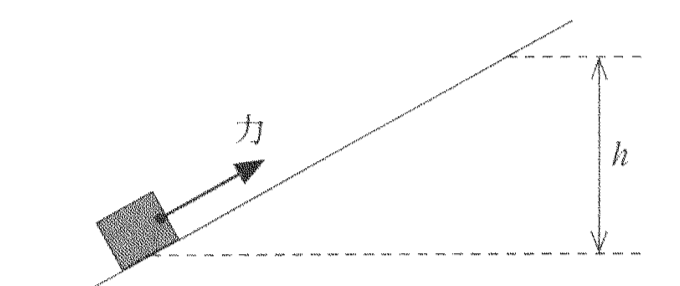
はじめの力学的エネルギー＋仕事＝後の力学的エネルギー

０[J]　＋　仕事　＝　mgh[J]

これを仕事について解くと、

仕事　＝　mgh[J]

となります。答えは①番です。

問２

AとBの引く力の合力（図の青）がCの力（図の緑）とつり合うと考えると、正方形なので、直角二等辺三角形の比（１：１：√２）となり、

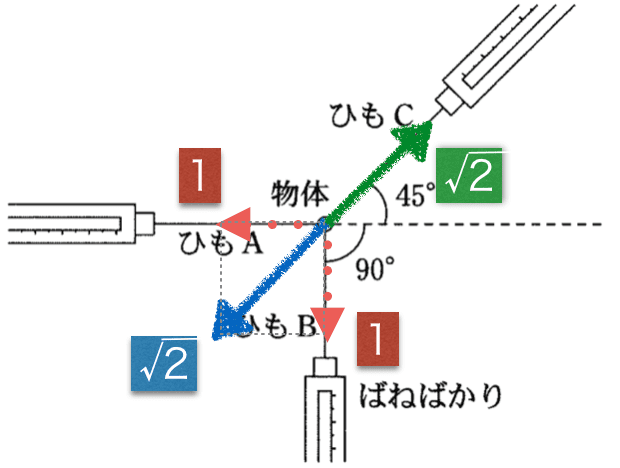
青と緑の力はつり合いの関係から同じなので、答えはA：B：C＝１：１：√２となります。答えは②番です。

問３

負の電荷をもつ電子の移動が静電気の原因なので、「ア」は電子です。またプラスとプラス、またはマイナスとマイナスのような同種の電荷は反発をするので、「イ」は反発しあうを選びます。電荷の単位は「クーロン」を用いるので、「ウ」はクーロンを選びます。答えは⑧番です。

問４

音速はおよそ340m/sですので「エ」は　340　を選びます。また直接届く音は１秒後に聞こえたということから、ピストルと観測者の間の距離は340m、

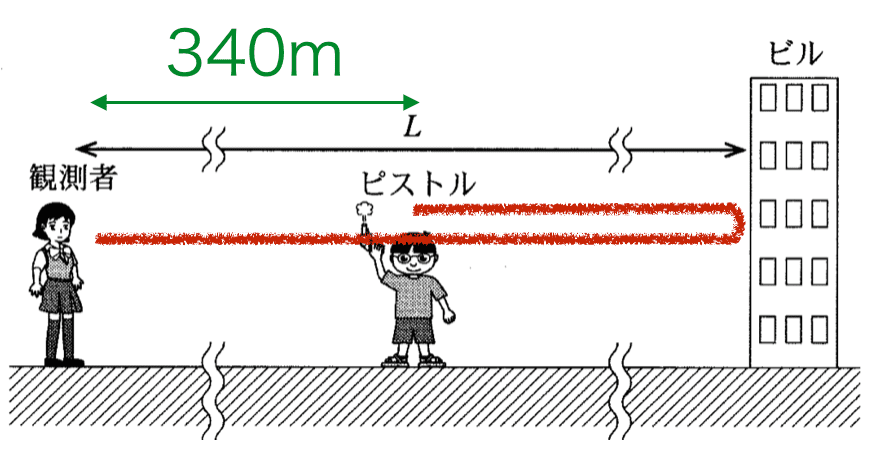
またビルに反射をした音は２秒後に聞こえたということから、図の赤の距離（往復含む）が340×2=680mということがわかります。ここから観測者とピストルの距離340mを引き（680−340=340)、残った３４０ｍには往復が含まれているので、２で割って片道の距離（ピストルとビルの距離）を求めると１７０ｍとなります。

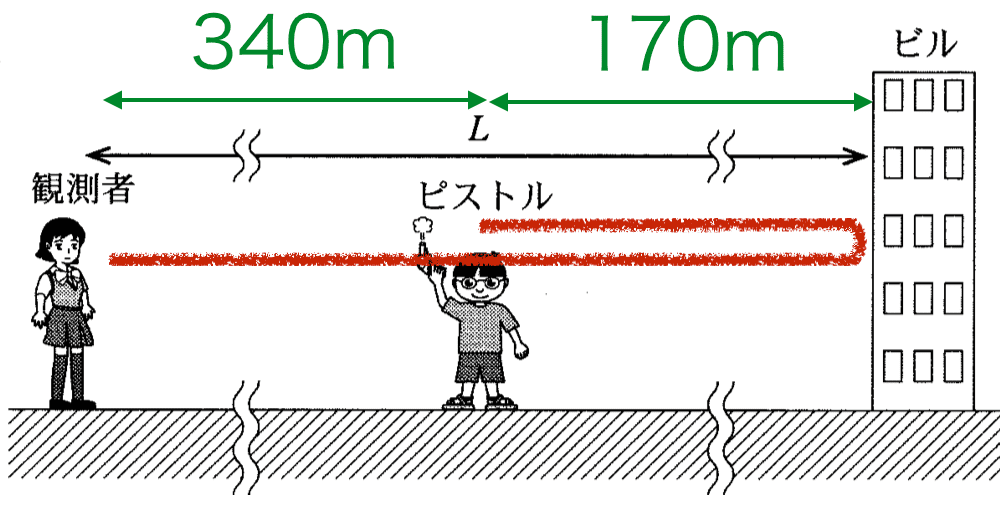
よって、観測者といビルの間の距離は、340+170=510mとなります。答えは⑤番です。

問５

Aが与えた熱量は、

Q_A=C_AΔT＝3.0×10²×（５０−３０）＝６.０×10³　[J]

となります。

また熱容量とは「ある物質の温度を１Kあげるために必要な熱量」であるので、温度があがりにくい物質ほど大きくなります。今回は同じ量の熱のやりとり（熱量）があったのにもかかわらず、Bのほうが温度変化が小さいため、Bのほうが熱容量が大きいということがわかります。よって答えは⑨番です。

第２問　A

cのグラフの２つの波を合成すると…赤が振幅が２倍になる場所、青が振幅が０の場所とわかるので、

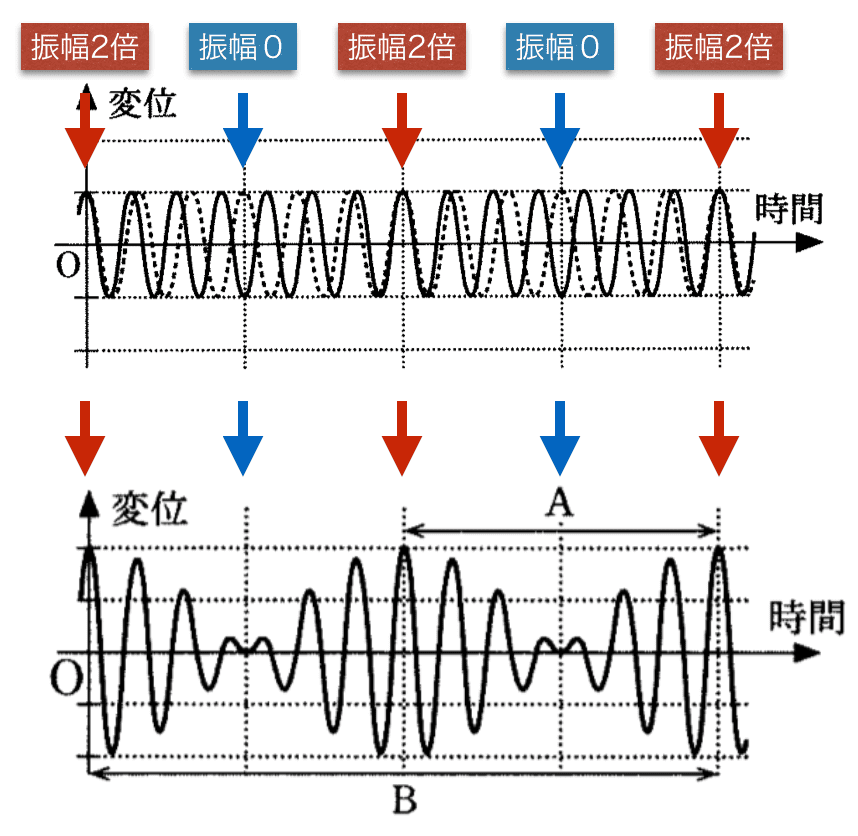
（エ）のグラフを選ぶことができます。また音が大きくなってから次に大きくなるまでの時間はAですので、うなりの周期はAです。答えは⑦番です。

問２

１秒間に聞くうなりの数は、うなりの公式から｜f₁−f₂｜ですので、周期は

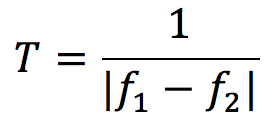
がうなりの周期となります。f1>f2なので絶対値をそのままとったものを選ぶと、答えは②番です。

＜参考　うなりの様子＞

第２問　B

問３

ジュール熱の公式から、

Q = IVt

またオームの法則(V=IR)をI＝V/Rとして代入すると、

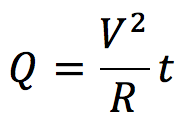
ここに数値を入れ、Rについて解くと、

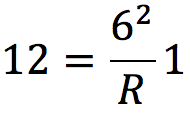
3.0Ωとなります。答えは④番です。

問４

次の抵抗の公式に

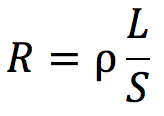
それぞれ表より値を代入すると、

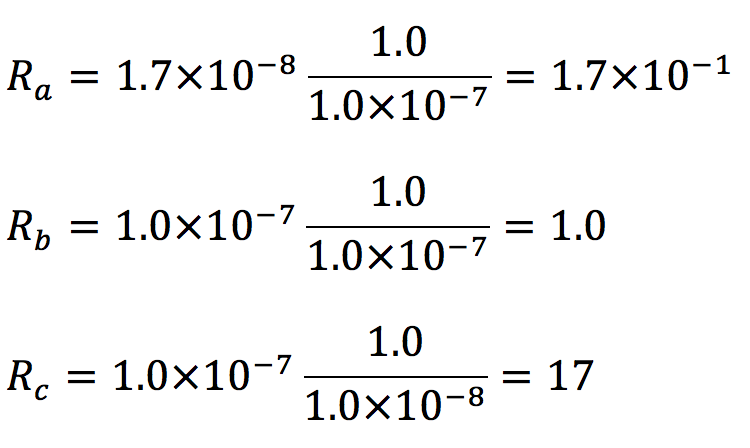
となります。よって抵抗値の大きさはC＞B＞Aとなり、答えは⑥番です。

第３問　A

問１

放物運動において最高点では速度が０になるので、

v=v₀−gt

　左辺に０を代入して、そのときの時間ｔを求めると、

０＝v₀−gt

　となります。答えは②番です。

問２

打ち出したときに小球が持つ速度は上向きにv₀と、水平方向に台車と同じ速度となります。

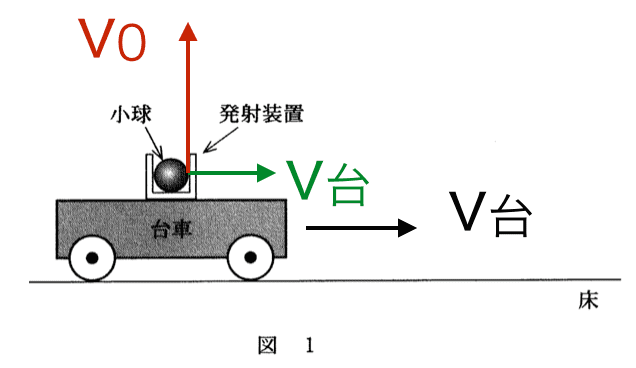
鉛直方向は先程と同じで加速度ｇが下向きにはたらくだけなので、最高点に到達する時間は変わりません。また打ち出されてから落下するまでに水平方向に力ははたらかないので、小球の水平位置は台車と変わりません。

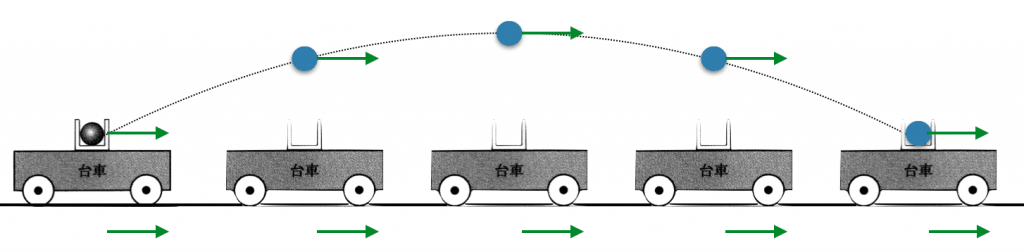
そのため台車の中に落下します。答えは⑨番です。

第３問　B

問３

Aのおもりにはたらく力を考えると、

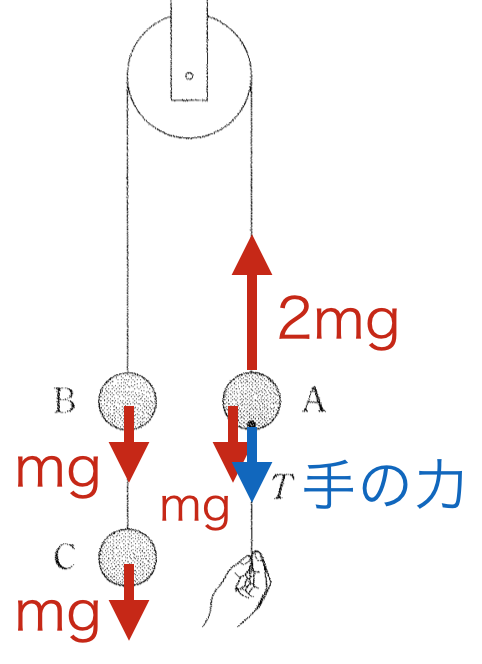
Aの重力ｍｇと手の力F（張力Tと同じ）で、左側の２つのおもり（２ｍｇ）を支える必要があるので、

手の力F＋ｍｇ＝２ｍｇ

（下向きの力＝上向きの力）

　これを手の力Fについて解くと、

手の力F＝ｍｇ

　となります。答えは④番です。

問４

A、B、Cの物体にはたらく力をすべて描き、それぞれについて運動方程式を作ります。

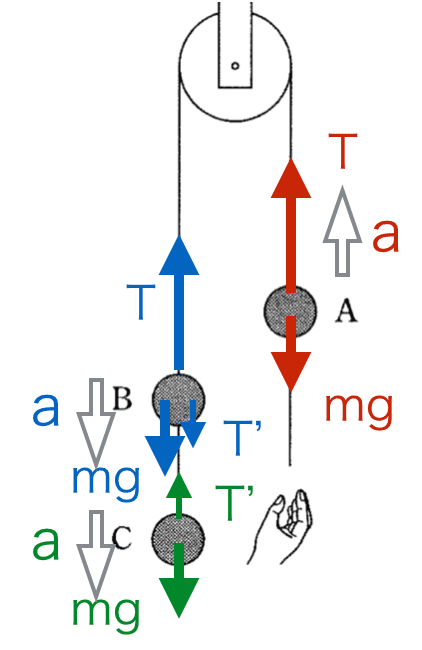
A：　ma = T‐ mg（上向き正）

B：　ma = mg＋T’‐T（下向き正）

C：　ma =  mg‐T’（下向き正）

図の中でポイントになるのは、ピンとはった糸の両サイドの張力は等しくなるということ（TとT’）、また加速度はすべて同じなのでaの１つの文字をあてているということです。T,T’,aが自分で置いたものじで、数式が３つあるので、解くことができます。

A、B、Cよりaを求めていきます。BとCを足してT’を消すと、

2ma = 2mg‐T

T = 2mg ‐ 2ma

これをAのTのところに代入すると、

ma = ( 2mg – 2ma ) −　mg

aについて求めると、

a=1/3g

となります。答えは①番です。

参考

運動方程式の作り方はこちらを参考にしてください。力のつり合いと混同しがちで、今回の問題もこのあたりの理解を狙っています。

全体の感想

物理基礎は本当に、「基礎」という感じですね。例年と難易度は変わらないと思いますが、最後の問題のように運動の法則の理解が問われるような問題だと、誤答をする生徒も多くなってくるのではないかと思います。みなさんはどう感じましたか？

参考

このような本を書いています。参考までにどうぞ。

[amazonjs asin=”405304118X” locale=”JP” title=”きめる!センター物理基礎【新課程対応版】”]

科学のタネを発信中！

ニュースレターを月１回配信しています。

[subscribe2]

フェイスブックページ（科学のネタ帳）の登録はこちらから

@kuwakoさんをフォロー