アツアツでお届け！当日解説センター物理(発展)2016（H28年度）
２時間ほど前に終わったセンター試験2016を、今日中に解説します。
まずは物理から解きます（追って物理基礎を解き始めます）。初めての方はまずはこちらのページを御覧ください。過去のセンター試験の解説や、おすすめの参考書についてまとめてあります。
物理基礎の解説はこちらからどうぞ。
[blogcard url=”https://phys-edu.net/wp/?p=23798″]
当日解いているため、間違いもあるかもしれません。
何かございましたら、お問い合わせからご連絡ください(^^)。
問題はこちらから見ることができます。
[blogcard url=”http://mainichi.jp/exam/center-2016/”]
物理 2016年（平成28年度）
第１問 小問集合
問１
同じ速さで打ち上げた場合、鉛直成分の初速度が大きな方が、滞空時間は長くなる。
参考：鉛直方向の距離の式
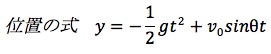
同じ速さで打ち出されている場合は、次の図のように角度の大きな小球１のほうが、
速度の分解をすると鉛直上向きの速度成分が大きくなる。
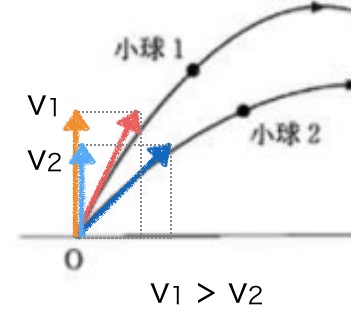
答えは①のT1>T2となる。キーワードはベクトルの分解。
問２
ア
不導体の場合でも、正に帯電した棒の付近には、表面の原子の中で自由電子が動き、負に帯電をするため、引力がはたらく。（例：風船を布でこすり、発泡スチロールの粒の側にもっていくと、発泡スチロールが吸い付く。）
イ
誘電分極：導体の場合には、自由電子が自由に動けるため、正に帯電した棒を近づけると、AやBの中にある自由電子（負）が表面まで移動をして、引力がはたらく。
ウ 静電誘導：(C)の状態で、Bは電子が集まっているので負に帯電している。またAはBに自由電子を供給したため、正に帯電している。このことから(ｄ)のように引き離しても、正に帯電したままである。
答えは①
参考ビデオはこちらを御覧ください。
問３
波の数式化の手順は、
ステップ１ 原点の振動を記述する
ステップ２ 時間をx/v遅らせる
の２ステップで作っていきます。
ステップ１ 原点の振動を記述する
グラフを見ると、原点の振動はsinになっているので、y=0.2sinωｔという数式になる。なお角振動数ωについては、周期との関係式ω=2π/Tより、グラフから周期を読み取ると２秒で１回振動しているので、
となる。よってy=0.2sinπtとなる。
ステップ２ 時間をx/v遅らせる
次に時間ｔをx/v遅らせる。これは原点を揺らした波が、ある位置ｘに到達するときにはx/v秒遅れてくることによる。よって、
y=0.2sin{π(t-x/v}となる。ｖに問題文より２を代入すると、答えは④番となる。
ポイント
波の数式化の問題。波の数式の基本形は、x=A□{ω(t-x/v)}。□にはsin,cos,-sin,-cosのいずれかが入る。ここを抑えておこう！詳しい式の作り方は、拙著『ぶつりの１２３波動編』を参考にどうぞ。
問４
運動量の保存から、物体Aの速さVを求めると（右向きを正）、
0 = −MV + mv
また図のようにAに対するBの相対速度は、
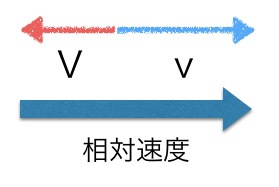
となり、その大きさは、
答えは④番。
問５
熱量保存の法則から、失った熱量＝得た熱量という式を作っていく。
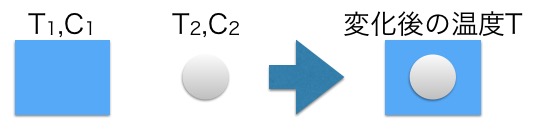
熱を失ったのは温度の高かった金属球、熱を得たのは温度が低かった水になるので、変化後の温度をTとすると
C2(T2 − T ) = C1(T − T1)
（金属が失った熱量＝水が得た熱量）
Tについて解くと、
となります。
このように、普通、熱の移動は必ず高いほうから低いほうへと移動し、その逆は起こらないので、これを不可逆変化といいます。振り子運動のように、位置エネルギーと運動エネルギーの変化が常に起こる変化を可逆変化といいますね。答えは⑤番。
第２問 電磁気
A 問１
まず変化前と変化後の絵を書きましょう。
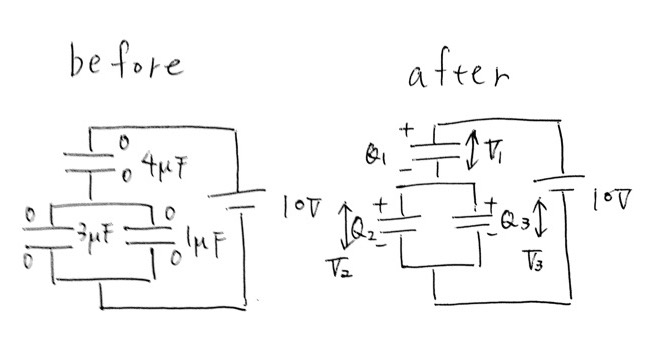
ここで３つの式を作っていきます。①電気量の式、②キルヒホッフの式、③電気量保存の式（島をみつけよう！）の３つとなります。
電気量の式より、
Q1=4μV1 ① 、Q2=3μV2 ② 、Q3=1μV3 ③
キルヒホッフの式より、
+10 −V1 −V2 = 0 ④
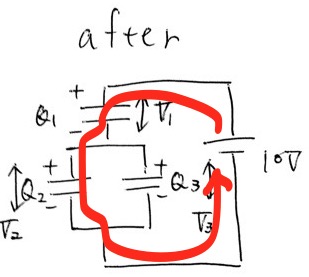
−V2 + V3 = 0 ⑤
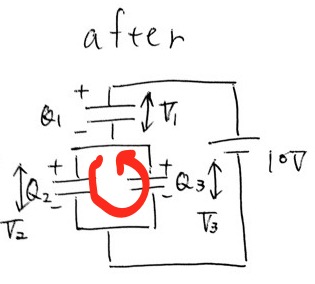
最後に電気量保存の式より、
0 + 0 + 0 = −Q1 +Q2 +Q3 ⑥
Q1 ＝ Q2 +Q3
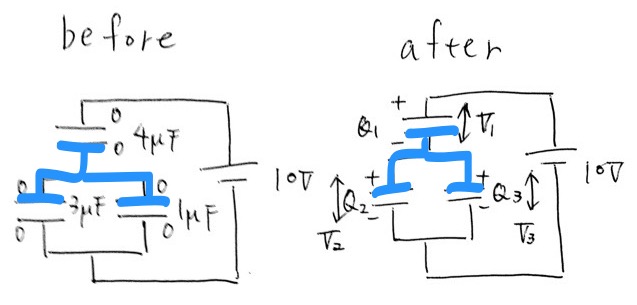
①〜⑥を連立すると、答えは①番。
ポイント！
コンデンサー回路の式は、①電気量の式、②キルヒホッフの式、③電気量保存の式（島をみつけよう！）の順番で作っていこう！
こちらは内部生にのみ公開している、ケン博士の動画シリーズです。お恥ずかしいのですが、参考にどうぞ(^^;)
：この解説に、一部誤りがありました。@dai7774さんに教えていただきました。ありがとうございました！ 平成28年1月20日
問２
コンデンサーの間の電場は、その公式から、E＝V/dなので、誘電体を入れようが入れまいが、Vとｄが同じであれば変わらない。また静電エネルギーの式は、
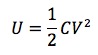
であり、コンデンサーの電気容量Cが誘電体（比誘電率εr）をいれるとεr倍されるので、εrUとなる。答えは②番。
抑えておこう！
コンデンサーの公式は、 Q = C V、C = εS/d 、E = V/d、U = 1/2CV^2の４つ！
B 問３
一様な電場の場合、Pは下方向に戻ってくるため、下向きの電場が必要になる。よって答えは③番となる。運動は放物運動（２次曲線）を描く。
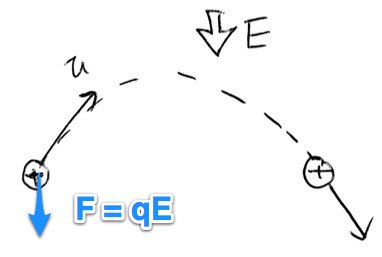
また一様な磁場の場合、紙面裏から表側にあれば、フレミング左手の法則より、円運動となりQに戻ってくる。答えは⑤番となる。
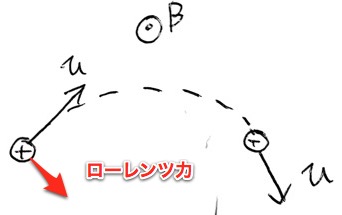
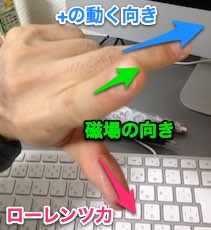
左手は写真のような感じ。中指が粒子の動く向き、人差し指が磁場の向き、親指が受ける力の向き。
参考動画
問４
問３で解説をしたが、運動方向と直行する方向に力を受ける場合、それは向心力となり、物体は円運動をする。そのため奇跡は円弧となる。また要した時間は、まず円弧の長さを求めて、次にそれをｖで割れば良い。
円弧の長さは次の図より、円の半径は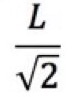
。
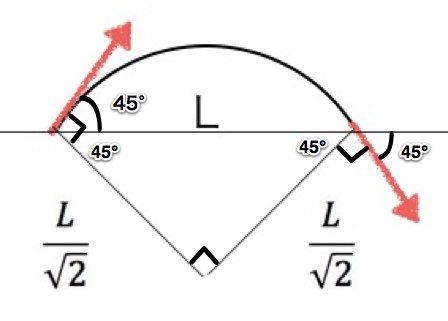
円弧はちょうど中心角が９０°になるため、円一周の長さの４分の１なので、
円弧＝２πｒ/4 =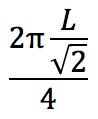 
となる。これをｖで割ると、正解は④番になる。
第３問 波動
A 問１
強め合う位置は、図のようにスピーカーの中心にあり、その両端に等間隔に1/2 λ（＝L）ごとに現れる。よって音の波長を求めて、それを半分にすれば良い。
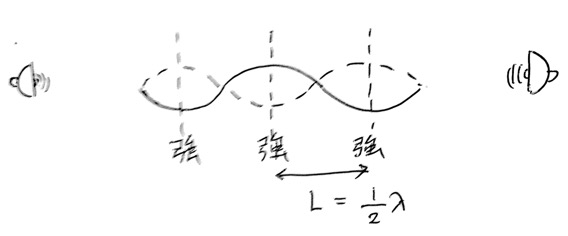
波の式（v=fλ）より、λ＝v/f = V/fo となる。これを半分にするので、答えは②番。
問２
ドップラー効果の公式（３ステップ解法）を使ってさっと振動数を求めてみましょう。
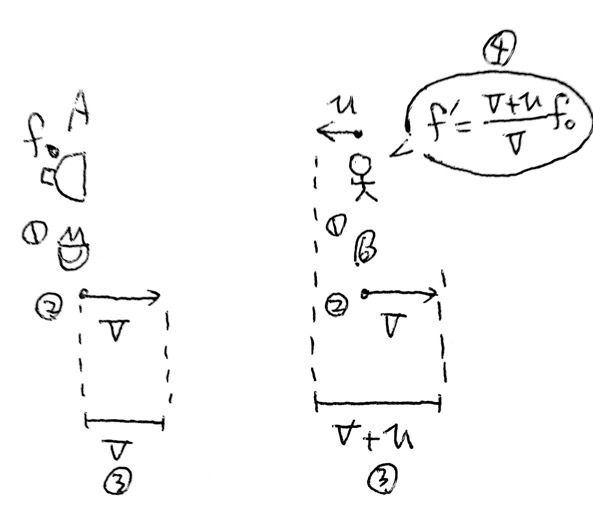
① 音源に口、観測者に耳を書く
② 口から耳にむかって音速Vを伸ばす。
③ それぞれの頭の間の長さを読んで、口分の耳×ｆ０に代入をする。
これらのことから振動数はこのようになります。
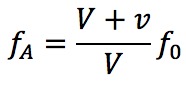
参考：ドップラー効果の３ステップ解法について動画でまとめました。
次にうなりについて求めてみましょう。１秒間に聞くうなりの回数は２つの音の振動数の差をとれば良いので（うなり＝|f1 − f2|）、Bの振動数も求めてみましょう。先ほどと同様に考えると、
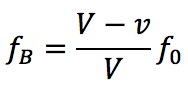
となります。よって、大きい方ｆAから小さいｆBを引くと、答えは⑦番になります。
B 問３
ウ
膜の厚さはｄなので、光の移動距離は往復で２ｄ。また光の速さはｃですが、膜の屈折率がｎなので、スピードは c/n となり遅くなります。よって時間は、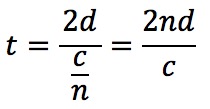
となる。
エ
経路差は２ｄであり、光路差は２ｎｄとなる。境界面Aで反射する光は位相が反転するので、強め合う条件は、
２nd＝ｍλ ＋ 1/2λ
（光路差＝強め合う条件）
ここでｍは０、１、２、３…
となる。が、注意！問題文にｍは「正の整数」と書いてあり、単なる整数ではない。正の整数は１、２、３…なので、０ではなく、１がスタートになるから、
２nd＝ｍλ − 1/2λ
（光路差＝強め合う条件）
ｍ＝１，２，３…
としておく（解答の選択肢を見ながら解くと、間違えないと思います）。
ここでλは空気中の波長であることに注意して、ｖ＝ｆλより、λ＝v/f=c/fを代入すると、
2nd = (m+1/2) c/f
となる。これが強め合う条件である。エでは時刻ｔを使って表してほしいので、この数式を整理すると、
2nd/c = (m+1/2) /f
となり、左辺がｔなので、右辺がその答え。よって答えは⑥番。
問４
オ
強め合う条件と弱め合う条件のまくの厚さを考えてみましょう。強め合う条件の膜の厚さは、
２nd＝ｍλ − 1/2λ より、
d = (mλ− 1/2λ)/2n 式①
弱めあいは、同様に考えると
d = mλ/2n 式②
となります。ここで、文章中に「膜の厚さを限りなく薄くするという」文章があるため、経路差が０の場合を指していることと読むことができます。
そのため、経路差０の条件に適合する、式②のｍ＝０の「弱め合い」がはじめにきて、次に「強め合い」次に「弱め合い」となります。
カ
膜を厚くしていくと、強め合います。これは上の式①のm=1が入った時の場合で、これがｄ１です。
：この解説誤りがあったため、@chokowaka2718さんからご指摘があり、直しました。 平成28年1月18日23時49分
キ
ｄ１は波長に依存するので、最も小さいということは、波長がもっとも短いものを選べばいい。答えは青色。
答えの番号は③番。
ポイント
波長は長い順番に 赤橙黄緑青藍紫 。おぼえかたは せきとうおうりょくせいらんし 。
第４問 力学
A 問１
円運動をするとき、向心力の役割をする垂直抗力は仕事をしないので、力学的エネルギーは保存する。力学的エネルギーの保存より、
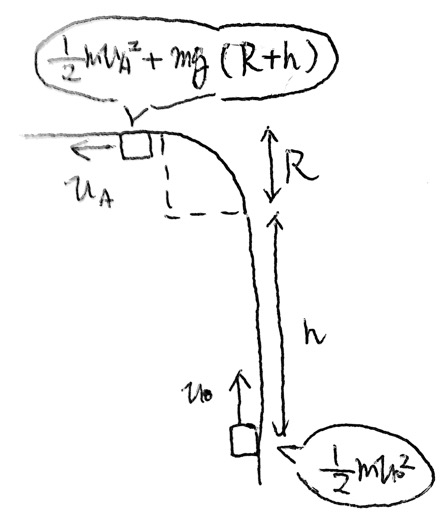
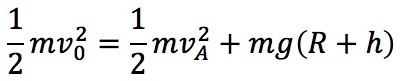
（はじめの力学的エネルギー＝Aでの力学的エネルギー）
これを解くと⑥番になる。
問２
これはよくある問題。Aを通過するためのギリギリの速度は、Aのときの速度が０ではなく、Aにきたときに向心力がｍｇのみであることが、通過するためのギリギリ条件。
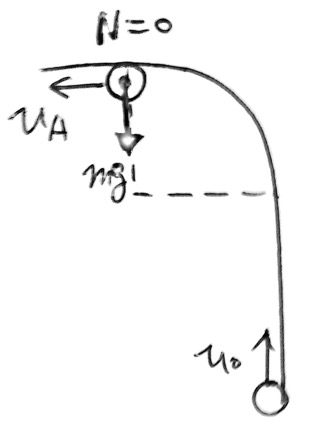
よってA点での運動方程式を作ると、
（運動方程式：ma = F）
これを解くと、
となる。答えは②番。
B 問３
小物体が滑っていないので、Mとｍは一体とみなしてかまわない。力学的エネルギーの保存より、
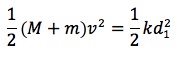
これをd1について求めると、答えは⑤番。
問４
滑る前は、２つの物体は１つの物体とみなして構わない。よって運動方程式より、
(M+m)a = kd
a =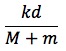 
となる。
また慣性力というヒントがあるので、慣性力について考えてみよう。ばねの縮がｄ2になったとき、上記の運動方程式と同じように計算すると、加速度はk2/(M+m)となる。
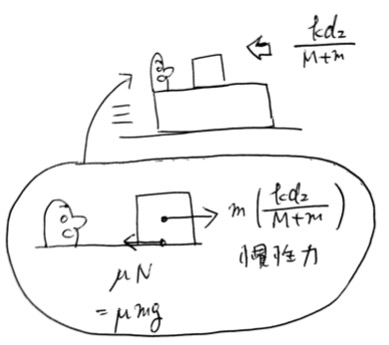
台とともに運動をしている人からこの様子を見ると、慣性力が加速度とは逆向きに物体ｍについて働いているようにみえる（慣性力の公式 加速方向とは逆向きにｍα）。
長さｄ2のとき、慣性力と摩擦力（最大摩擦力）が釣り合っているとかんがえられるため、
左向きのちから＝右向きの力
ｄ2について解くと、
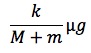
答えは⑨番。
第５問 熱力学（選択）
問１
AとBについて、それぞれ状態方程式（PV＝nRT）を立てましょう。
PA VA = nRTA
PB VB = nRTB
それぞれ圧力についてもとめて、PA /PBを求めます。
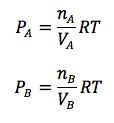
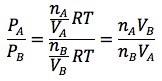
答えは③番。
問２
表にまとめてみましょう。
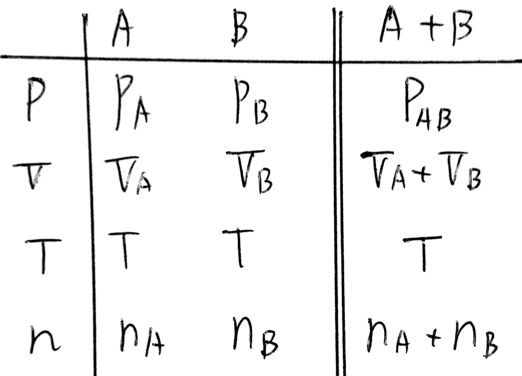
体積とモル数は単純に足し算になりますが、圧力や温度は単純に足し算してはいけません。まず今回の場合、温度は外部との熱のやり取りをするので、変化がなくTです。圧力はわからないためPABと置いておきましょう。この状態で状態方程式を使います。
PAB(VA + VB) = (nA+nB)RT
この式と、先ほどつかったそれぞれの容器での状態方程式を使って、
PA VA = nRTA
PB VB = nRTB
PABについて解くと、答えは③番。
問３
同じ種類の気体なので、内部エネルギーはｎCvTとなります（Cvは定積モル比熱）。ここで、内部エネルギーの変化はnCvΔTと表すことができますが、今回のコックの開け閉めにおいて、温度は一定に保たれています。つまりΔTがそれぞれの気体で０になります。このことから、内部エネルギーの変化はΔT＝０なので、０です。
ひっかけのような問題ですね（＾＾；）
答えは⑤番。
第６問 原子物理（選択）
問１
ア 光電効果は光の粒子性を示す現象です。
イ これは覚えておきましょう。光子の持つエネルギーはhνです。
ウ 光電効果の公式（hν＝1/2 mv2 + W ※vは粒子の最大の速度）より、E−Wとなります。
答えは⑥番です。
問２
素子電圧を見ると、Vo[V]になっているのが図２からわかります。これは一番勢いのある、飛び出してきた光電子を止めるために必要な電圧を示しています。よってエネルギーの保存則より
1/2 mv2 = eVo
ｖは光電子の最大速度です。これをvについて解くと、答えは⑧番です。
問３
素子電圧の値が変化していないので、光電管にあてている光の波長（振動数）は同じものをつかっていることがわかります。そのかわり、光電子の量そのものが減っているので、より暗い光をあてたことがわかりますね。答えは④番です。
感想
ひとまずすべて解き終わりました！現在の時間は23時49分です。円弧になって動く粒子の問題が難しかったでしょうか。その他は昨年と同様に広く薄く出題された感じでしたね。みなさんはいかがでしたか？続いて物理基礎を解きたいと思います。験生の皆さん、もしよければご活用ください！
[blogcard url=”https://phys-edu.net/wp/?p=23798″]
関連リンクの紹介
→ ネット予備校を主催している田原先生のサイトで、センター物理の無料講義動画も見られます。
→ 過去のどこよりも早く！はこちらを参考にしてください。
・平成２７年度（２０１５年） 物理基礎 物理（発展） ※ ときはじめ１月１８日８時３０分〜解き終わり１月１９日１時３５分
・平成２６年度（２０１４年） 物理１
・平成２５年度（２０１３年） 物理１
・平成２４年度（２０１２年） 物理１
→ センター物理に関する参考書を書きました！こちらより御覧ください。
[amazonjs asin=”405304118X” locale=”JP” title=”きめる!センター物理基礎【新課程対応版】 (きめる!センターシリーズ)”]
→ 更新情報はツイッターより確認してください。
お気楽にお問い合わせください。
・ご感想・ご質問はこちらまでどうぞ(^^)
・ニュースレターではブログには載らない情報を配信しています。
[subscribe2]
