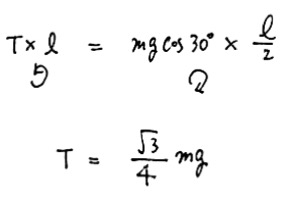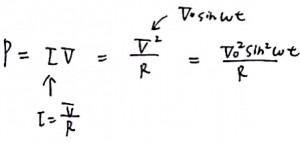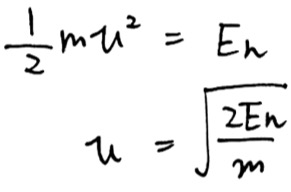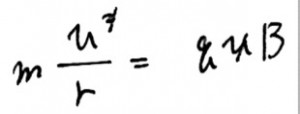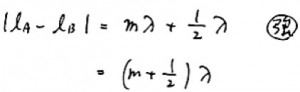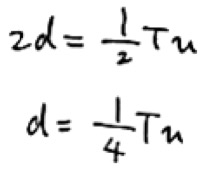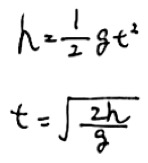即日解説！2015センター物理（発展）
今年もやります！センター試験 物理・物理基礎はこちらを御覧ください！
[blogcard url=”https://phys-edu.net/wp/?p=19709″]
センター物理（発展）
※ センター試験2015、物理基礎・物理の解説を行います！
初めての方はまずはこちらのページを御覧ください。
大問題などはすべてこちらにまとまっています。当日解いているため、間違いもあるかもしれません。
何かございましたら、お問い合わせからご連絡ください。問題用紙はこちらをご覧下さい。
第１問 小問集合
問１
回折は波が回りこむ現象のことをさします（パソコンの人は湯浅先生の高校物理イメージ教材から回折の動画を見て下さいね！）。５番は波が回りこむことによって起こる現象なので回折と関係があります。
①は、波の媒質が振動していることにより、ゆらゆらと見えます。
②は、物体の持つ固有振動数のことですね。
③は音速と気温、そして屈折率の関係。よく出ますね。
④は波の重ねあわせですね。自由端反射になるのが、水の波の特徴（ばねの動きの動画を撮影しました）。
⑥は光の散乱と関係がありますね。センターでは頻出です。
⑦はドップラー効果ですね。関連動画はこちらです。
ポイント！
回折・反射・屈折・干渉・散乱・分散などなど、
波の性質で起こる身近な現象はセンターではとくによく聞かれます。
誤っている選択肢も含めて、必ず調べておきましょう。教科書が活躍します！
問２
はじめにQ’が＋（正）なのか、−（負）なのかを考えてみましょう。右下の電荷Q’が＋であった場合と、−であった場合についてそれぞれ考えます。もしQ’が＋ならば、次の図のようになり、
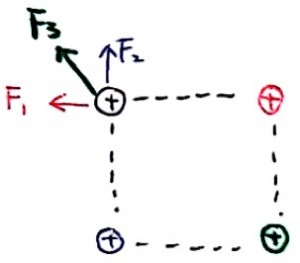
この場合、左上の電荷qは絶対に左上のほうに動いてしまいますよね。止まることがないので誤りです。
ではQ’が−ならどうでしょうか。次の図のような力関係になり、これならF1とF2の合力がF3とつり合うことで、バランスがとれそうです。
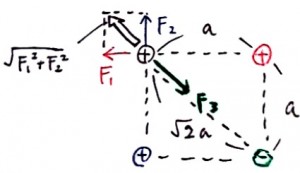
式１
実際に数字を入れて計算をしてみましょう。静電気力の公式を使うと、
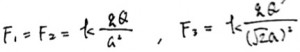
となります。これらを式１に代入して整理をしていくと、
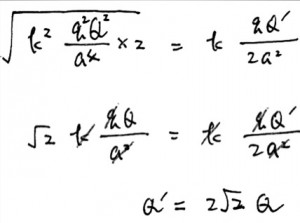
答えは４番！です。
・・・とおもいきや！
ちょっとまった。
たしかQ’はマイナスでしたよね。答えはマイナスのついている８番です。
今回の問題の解き方のように、電荷の持つマイナスとプラスは力の向きと関係があるので、絵の中に描いておき、
計算をするときは、力の大きさを求めることに専念して、電荷の大きさのみを使って計算をしていくことが、問題を間違えないコツです。
でも最後にマイナスをつけるのを忘れないようにしましょうね。
高校物理ではベクトル量をいかにさばいていくのか？それがとても大切になります。
問３
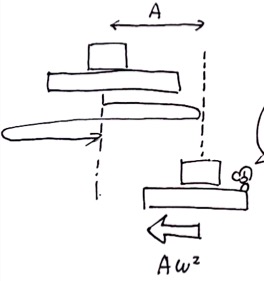
慣性力の大きさは、乗り物の加速度の大きさに比例した力の大きさmaでした。
そのため台の加速度aがもっとも大きくなる場所を考えれば良いということになります。
台がもっとも加速するのは、振動の両サイドにきたときです。
単振動と同じですね。
このときの加速度は最大となり、a=Aω^2となります（単振動は円運動の影、最大値は円運動の加速度の公式を使うことで求められます）。
よって慣性力F1は、F1 = ma = mAω^2となります。
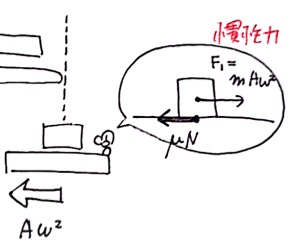
またこのときの台に乗った人の立場で考えると、次の図のように滑り始める直前では摩擦力と慣性力F1がつりあっていることになるため、力のつり合いをたてることができます。
μN = F1
（左向きの力＝右向きの力）
N＝ｍｇなので、F1＝μｍｇとなります。ちなみに動き出す直前の場合には、静止摩擦係数を使いましょうね。
問４
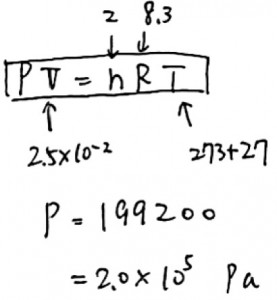
なんだこりゃ！といった問題。おそらく難易度調整に使われたのでしょう。状態方程式に代入して、圧力を求めましょうね。
計算間違えだけは注意が必要です。正解は８番。
問５
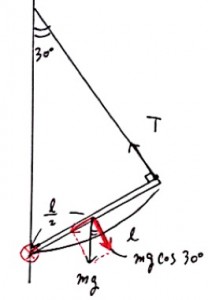
これは基礎的なモーメントの問題ですね。ちょうつがいの部分を回転軸として、モーメントのつり合いを作っていきましょう。
答えは２番。よくモーメントの問題だと、力のつり合いもつかって、蝶番にはたらく力の大きさや向きなどを考えさせる場合もあります。
今回は簡単でしたが、そういった問題も解けるようにしておきましょうね。
また力を移動させてモーメントのつり合いを作る場合もあります。いろいろな問題でなれておきましょう。
第２問 電磁気
A 問１
ダイオードの問題で、慣れていないと焦ってしまったかもしれませんね。ぼくもダイオードをセンターで出すんだ！と驚きました。
注意！
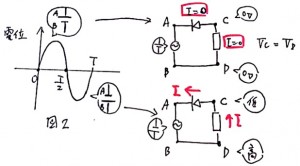
問題文にかいてあるように、ダイオードは電流を一定の方向にしか流さないという性質があります（整流作用）。
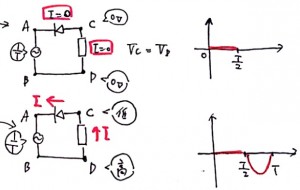
今回の問題だと、ダイオードは左向きには電流が流れますが、右向きには電流がながれません。
そのため、図２で０〜T/2の間は電圧がAのほうが高いので、ダイオードが邪魔をして電流が流れません。
電流が流れなければ、電圧降下もないので、CとDの電位は等しくなります。
またT/2〜Tの間では電圧がBのほうが高くなるので、回路に電流が流れます。
すると抵抗では電圧降下により、CのほうがDに比べて電位が低くなります。
これらのことから選べるのは５番ということになります。
問２
問１のグラフをみると、ちょうどsinのグラフの谷の部分だけ電圧がかかり、抵抗に電流が流れることがわかります。
このことからダイオードがなかったときの場合の交流電流による消費電力の時間平均値の半分の消費電力になっていることがわかりますね。
このため、まず普通にダイオードがなかった場合の消費電力Pの時間平均値Pバーをもとめて、それを半分にしてしまいましょう。
交流電源の電圧Vは、V=V0sinωtとあらわすことができます。消費電力の公式に代入すると、
となります。また倍角の公式をつかって、式変形をすると、
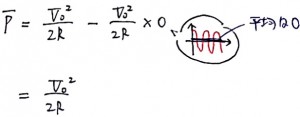
ここで消費電力の平均値をとると、cos2θはならされて０となり、次のようになります。
答えは、これの半分になるので÷２をすると、３番の答え（V0^2/4R）となります。
問３
難しそうにみえますが、簡単な問題です。
これはサイクロトロンに関する問題ですね。隙間を通るたびにVの電圧で加速をされます。
１回隙間をとおるときにもらう電気的な位置エネルギーは
U = qV
です。ｎ回通ればｎ倍されますから、nqVとなります。この粒子ははじめにE0のエネルギーをもっていたので、E0を足して、
答えは１番（E0+nqV）となりますね。
問４
これも難しそうに見えるかもしれませんが、簡単です。
まずはEnの運動エネルギーをもっているならば、そのきの速さは
となります。
また半径を知りたい場合には、円運動の運動方程式（ma=F）を作りましょう。円運動の加速度はv^2/r、ローレンツ力はqvBです。
(ma = 残った力)
ｒについて解くと、
答えは１番となります。
第３問 波動
A 問１
振動数ｆが等しいということをいっているので、波の式をそれぞれの境界でつくってみましょう。
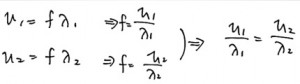
それぞれの式をｆについて解いて、右辺を等式で結ぶと、答えは６番になります。
問２
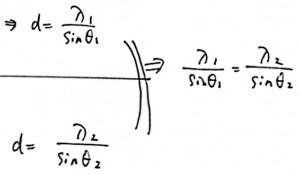
それぞれの境界でｄと波長の関係を考えてみましょう。まず上の境界面では、
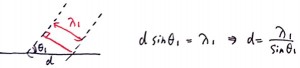
となります。波長の位置に注意をしましょう。次に下の境界面でも同様に、
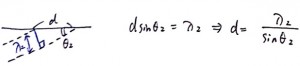
となります。ｄがお互い共通なので、dについて解いて、等式で結ぶと、
となります。答えは２番。
注意！
屈折の公式はおぼえている生徒が多いと思いますが、
どのように導かれたのか？というものセンター試験では多くでてきます。
凸レンズの公式、ヤングの経路差などなど、
ぜひ導出方法から学び直しましょう。
B 問３
A点とB点では逆位相の波がでてきます。このため強め合いの条件式は次のように、
いつもなら弱め合いとなる条件になります。
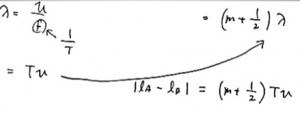
まさにこれが答えなのですが、選択肢に同じものがありませんね。λが問題文で与えられていないので、
λを問題文で使っていい記号に書き換えましょう。波の式を使います。
このようにλ＝Tvとなります。これを代入しましょう。
答えは６番。
問４
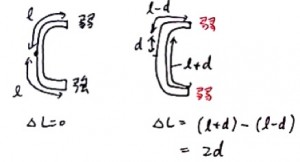
これは水路から出てくるA点B点において、波が同位相になったことを示しています。
例えば上にｄずらしたとき、このときの経路差は２ｄとなります。
最小のずらし方で同位相になったということは、いままでは1/2λ=1/2Tvずれていたので（出口で逆位相になっていた）、
それが治ったということですから、この２ｄの中でずれを治す部分、1/2Tvが入っていることになります。
答えは２番。
ポイント！
今回の問題は経路差を見ていくことがやはり決めて！
A点B点の右側の条件は全く変わっていないので、
ずらしたことにる水路の部分での差を考えます。
最小のずらし方ということから、1/2λに気がつくかどうか。
人と差のつく問題です。
第４問 力学
A 問１
これは大丈夫ですよね。放物運動では鉛直方向のみ加速度ｇがはたらきます。水平方向の速度は変化しません。よって
t = 道のり÷速さ ＝ L/v0
となります。答えは２番。
問２
これも初歩的な問題ですね。壁にぶつかったときにボールにはたらく力は水平方向にはたらきます。壁から鉛直方向の力ははたらきませんから、
このボールはぶつかったあとも下向きにｇの一定の加速度で落下を続けます。
もともと高さはｈだったので、等加速度直線運動の公式を使えば、
となります。
問３
力学的エネルギーが減少をするポイントは、壁にぶつかったときですね。
壁の前後で、速度がどのようになるのかを見てみましょう。
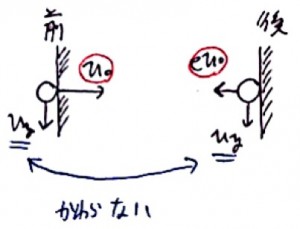
このように、壁にあたることによって水平方向の速さがv0からev0へと小さくなってしまいます。
縦方向の速さはとりあえずvyとしましたが、これは変化しません。
このことから失ったエネルギーは、
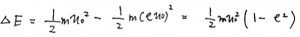
となります。答えは５番。
B 問４
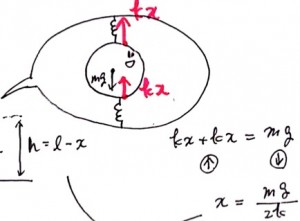
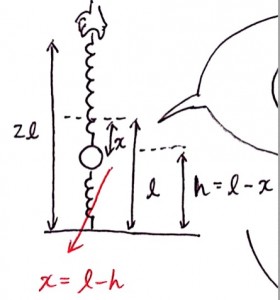
上のバネの伸び、または下のばねの伸びをｘとすると、次の図のように高さｈはl-xで表されることがわかります。
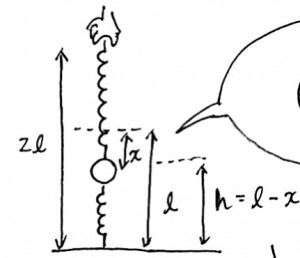
次にｘについてもとめるためにボールにはたらく力を全て書きましょう。
ポイント！
顔をかいて、物体の気持ちになってみよう！
ばねはもとの長さに戻ろうとする方向に力がはたらきます。
つまり下のバネは上に押し、上のばねは上に引っ張ります。
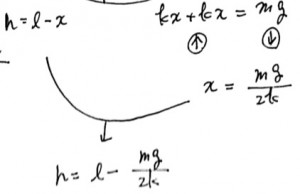
このことから、図の右に示したように、力のつり合いより、2kx=mgとなります。
先ほどの高さの式（h=l−x)に代入してみると、
となります。答えは１番。
問５
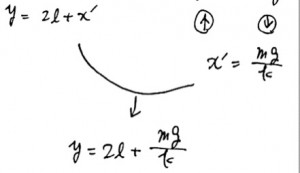
まずはｙについて求めてみましょう。このときのバネの伸びをｘ’とすると、
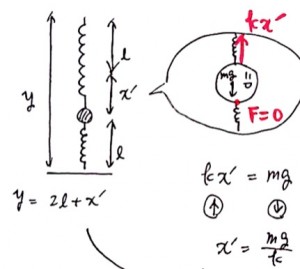
となります。またボールにはたらく力について考えると、下のばねは伸びていないので力を出しません。
よってｘ’は図の右に示したようになります。２つの式を合わせてｙについて求めると、
となります。
続いて仕事について考えてみましょう。仕事は力学的エネルギーを変化させるものなので、
はじめの力学的エネルギーと終わりの力学的エネルギーの変化が大切です。それぞれの力学的エネルギーを書き出していきましょう。
式１
はじめの力学的エネルギーは、弾性エネルギーのみです。２本ばねがついているので×２としました。
またばねの伸びについては、選択肢にあわせてl−hを使いました。図を見ればわかりますよね。
おわりの力学的エネルギーは上のばねの弾性エネルギーと位置エネルギーです。
弾性エネルギーについては、やはり図をみて伸びを2l-yとしました。
エネルギーの保存を示す式１を、仕事Wについて導くと、
となりますね。答えは６番です。
→ エネルギーの保存はたてられるかな？間違ったひとはこちらの動画授業をチェック
第５問 熱力学（選択）
問１
これは簡単！答えは２番です。
熱力学第一法則より、Q=⊿U+W。断熱変化は外から熱がやりとりされない過程のことなのでQ＝０。
また等温変化は温度が変化しない、つまり内部エネルギーの変化がないので⊿U＝０ですね。
問２
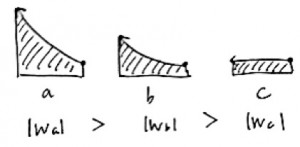
これも簡単！P-V図の性質を知っていれば解けますね。
ポイント！
P-V図は囲む面積が気体がする、またはされる、仕事の量を示します。
体積が膨張するときは気体が仕事をする、収縮する場合には、気体は仕事をされる。
今回の変化はすべて仕事をされる変化になります。
面積を見てみると、a>b>cの順番になっているので、答えは６番です。
問３
最後はセンターらしいグラフを選ぶ問題ですね。
まずわかりやすいのが等温変化。温度が同じなので、体積が減少しても温度はかわりません。よってｂはオのグラフのようになります。
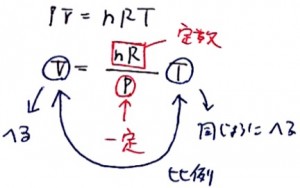
次に定圧変化をみてみましょう。状態方程式(PV=nRT）を変形すると次のようになります。
この式をみながら検討をしていきましょう。nRは定数です。定圧変化の場合はPも一定なので決まった数字です。
定数はどうでもいいので、その他の部分であるVとTの関係を見ると、体積が減少すると、
温度Tも「同じように」減少します。比例関係にあるからです。
よって選ぶV-Tグラフは直線になったもの、ウですね。曲線の形で現象をしません。
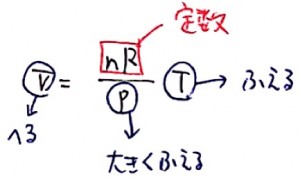
最後に断熱変化です。断熱変化の場合は、熱力学第一法則により
0 = ⊿U＋W
−W＝⊿U
となります。つまり仕事をされると内部エネルギーは増えていきます。内部エネルギーが増えていくカのグラフを選ぶというわけです。
なおPーV図をみるとわかるように、された仕事の面積は一定の増え方ではなく、グイーン！と増えていますから、
それに合わせて内部エネルギー、つまり温度も急激に増えていきます。直線にはなりません。
その他にも別解として２つあげておきましょう。
（別解１）
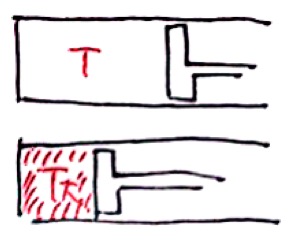
断熱変化は雰囲気で選ぶことができます。先ほどと同じように状態方程式で検討をすると、
V,P,Tが変数で３つだと関係性がよくわかりません。しかしp-V図を見てみると、体積が減ると圧力が急激に増えているのがわかります。このことから温度Tは大きくなりそうなので、カのグラフを選ぶことができます。
（別解２）
実験をしたときを思い出してみましょう。閉じ込めた気体を急激に圧縮すると、温度があがりましたよね。
圧縮発火器などで学校でやったことがあると思います。温度が増えているグラフはひとつしかないので、選びやすいですね。
第６問 原子物理（選択）
問１
ポイントは正電荷が狭い範囲に集中していたらどうなるか？というところです。選ぶものは反発をしているものなので１〜３番の中からになります。
また原子核がより狭い範囲にある場合には、３番のようにある場所でのみ弾き飛ばされるような絵になることが予想されますね。
答えは３番。
問２
これは知識問題というか、原子分野をやっていれば解けると思います。
アはエネルギーを失っていくというものでした。イは光を出すということで光子ですね。光電子とは光電効果と関係がありましたね。
問３
これも簡単！？量子条件より
2πr=nλ
また物質波の式λ＝h/mvを使うと、
2πr = nh/mv
となります。答えは６番
選択問題と考えると、これは第６問を選んでおいたほうが正解だったかもしれませんね！
ケン博士の感想
新課程のはじめだということで、
思ったよりも簡単ではなかったように思います。
ちょっと以外だったのが、フレミング左手の法則や右ねじの法則が
物理基礎にも出てきませんでした。
（昨年提示された問題例でも示されていました）
これも出ませんでした。
教科書のつながりという面で考えると、
問１では波の性質を問われており、教科書をよく読んだり、
解けるような問題がみられました。
公式を導出する途中のような問題、第３問の屈折のものや、
そういった内容理解に関する問題が見られることも、
しっかりと教科書を読み込んだ生徒が解けるような問題であったと
旧課程の物理１と比べると、計算に時間のかかるもの、
そういった面でも広く薄くの出題になっていますね。
物理基礎も解きました！
こちらからどうぞ。
また更新情報は随時ツイッターにて流しております。
こちらも同時にご確認ください。
※ センター試験対策の参考書を書きました。
来年度受けるよ！という人は参考にしてくみてください。
[amazonjs asin=”405304118X” locale=”JP” title=”きめる!センター物理基礎【新課程対応版】 (きめる!センターシリーズ)”]
過去の「どこよりも早く！」はこちらを御覧ください。
高校２年生におすすめしたい参考書をまとめました
ニュースレター
・ニュースレターはブログでは載せられない情報を配信しています。
[subscribe2]
