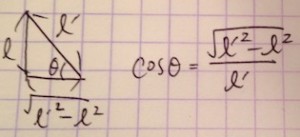２本のバネのセンター物理追試！「見える化」せよ！物理の問題を解き明かす思考のストーリー
サイエンストレーナーの桑子研です。毎日が実験。
物理って、ただ公式を覚えるだけの科目だと思っていませんか？実は、物理の面白さは、問題を解くための「思考のストーリー」を組み立てるところにあります。どの公式を選び、どんな手順で解き進めるか。まるでミステリー小説の探偵になった気分です。今日は、センター試験の過去問を例に、物理の問題を解くための最高の思考法、そしてそこに隠された科学のロマンを一緒に探ってみましょう。さあ、君も名探偵になって、この謎を解き明かそう！
今日はセンター試験（平成25年度 追試 第四問）から、運動方程式や力のつり合いがよくわかっているかどうかが、よくわかる！そんな問題について、みんなと考えてみようと思います。
みなさんはこんな問題、解けるかの！？
問題
ばね定数がｋで長さが同じ２本のバネを細長い帯でつないだものを用意し、
その両端を水平でなめらかな床の上の２点P，Qに固定した。
このとき、２本のばねはともに自然の長さになっていた。
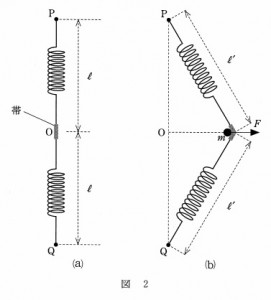
図２(a)はこのときの様子を真上からみたものである。
PQの中点を０とすると、OPとOQの長さはともにl（小文字のエル）であった。
この状態から点０の位置で小球を帯に当て、図２(b)のように，小球を床に
そって右向きに手で引いて静止させた。
このとき、点Pおよび点Qから小球までの距離は、ともにｌ’であった。
ただし、ばねと帯の質量は無視でき、帯は伸び縮みしないものとする。
> 問 図２(b)の状態で、手が加えている力の大きさFを表す式として正しいものを、次の①〜⑥のうちから一つ選びなさい。
さて、みんなはこの問題解くことができたかの？
どのような解法を使ったかな？それでは解説をしよう！
解説
力学の問題をみたときに、考えるのはまずはじめにエネルギーの保存や運動量の保存をつかって解くことができないかどうかです。
なぜこの思考が重要なのでしょうか？物理の世界では、保存則はまるで最強のチートコードのようなものだからです。もし保存則が使えるなら、複雑な力のやりとりを一つ一つ追う必要がなくなり、問題を一気にシンプルにすることができます。しかし、全てのミステリーにチートコードが通用するわけではありません。
もしそれらが使えなければ、力と運動の３ステップ解法を使って、運動方程式もしくは力のつり合いの式をつくって解いていきます。
それでは今回の問題を見ていきましょう。
エネルギーの保存を使う問題のポイントは、
・１つの物体に注目していること、
・前後の状況が問われていること、
の２つです。
今回の問題では、単に力の大きさが問われており、前後の様子は問われていません。
そのためエネルギーは必要なさそうですね。
また運動量保存が使えるかどうかの判断は、
・複数の物体が相互に力を及ぼし合っているか、
です。今回は１つの物体にしか注目をしていないようなので、運動量保存も出番はなさそうです。
というわけで、力と運動の３ステップで解いていきます。
１ 物体にはたらく力をすべてかく。
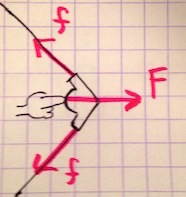
物理の問題は、目に見えない力を「見える化」することから始まります。力を正確に図に書き込むことで、問題の本質がクリアに見えてきます。今回はボールと帯がでてきますが、ボールと帯を１つの物体として、この物体にはたらく力を全て書きましょう。
図のように手が押す力、バネが引く力×２の３本の力がはたらいているのがわかりますね。
２ 静止（等速） か 加速 かを判断する
これは、ニュートンの第一法則か第二法則かを判断するステップです。物体が動かない（静止）か、速度が変わらない（等速）なら第一法則、速度が変化する（加速）なら第二法則を使います。今回は物体が静止しているので、第一法則、つまり「力のつり合い」を使います。
３ 力のつり合いの式を作る
静止している場合は、力のつりあいの式を作りましょう。
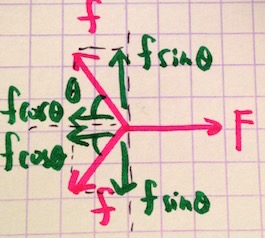
ばねが出している力を上下左右の方向に分解します。角度がわからないので、図の場所をθとしました。物理では、このように未知の量を一時的に「仮の名前」で呼ぶことがよくあります。
このとき左右方向の力はつりあっているので、
fcosθ+fcosθ=F
左方向の力＝右方向の力
という数式をたてることができます。このことからF＝2fcosθが答えなのですが、問題文で与えられていないｆやθは使ってはいけません。
さて、ここからが物理の真骨頂。**「未知のものを既知のもので表現する」**という作業です。まるで暗号を解読するように、与えられた情報だけで答えを導き出します。
そのため、これらを取り替えていきます。
例えばｆはばねの力なので、ばねの伸びに比例します（F＝ｋｘ）。
ばねの伸びは(l’ – l )なので、
f＝k(l’ – l)
となります。
次にθが難しいそうに見えますが、θに関しては、目線を引いて大きく見ると、直角三角形があることに気が付きますね。
よって、これらをF=2fcosθに代入すると、
F = 
となり、答えは６番となります！
いかがでしたか？解法の選び方にぜひ注目をしてといてみてくださいね！
この問題が解けた君は、単なる暗記ではなく、**物理の「思考の型」**を身につけ始めている証拠です。物理の面白さは、このように目の前の現象を論理的に解き明かすプロセスにあります。ぜひ、他の問題でもこの「思考のストーリー」を意識して取り組んでみてください。君の物理の学びが、もっともっと深く、面白くなるはずです。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
