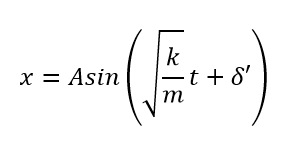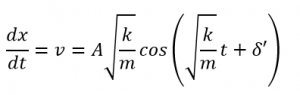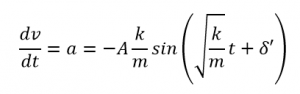高校物理のモヤモヤ解消！単振動をグラフから読み解く（高校物理と微積分）

サイエンストレーナーの桑子研です。毎日が実験。

高校で物理を学んでいる皆さん、「この現象って、もっとスッキリ説明できないのかな？」とか、「なんでこんなに回りくどい言い方なんだろう？」と感じたことはありませんか？ 実は、高校物理の教科書では、数学の学習進度に合わせてあえて「微積分」を使わずに説明がなされています。でも、これって、実はちょっともったいないことなんです！ 微積分を味方につけると、これまで複雑に見えていた物理現象が、まるで霧が晴れるようにクリアに見えてくることがたくさんあります。

このコーナーでは、まさにそんな「微積分を使うと、もっと深く、もっと直感的に理解できる物理のテーマ」を一つずつ掘り下げていきたいと思います。今回は、物理でよく登場する「ばねの単振動」にスポットを当てて、微積分の力を借りてその動きの秘密に迫ってみましょう！

単振動の数式と物体の振動イメージ、そして微積分の力

前回、私たちは「－定数×変位」という力が物体に働くと、その物体が「単振動」をすること、そしてその運動を微積分を使って数式で表現できることを学びました。

その時の変位の式がこれでしたね。

x=Asin(ωt+δ′)

※ここで δ′ は積分定数で、物体の振動が始まった瞬間の位置や速度を示す「初期位相」を表します。

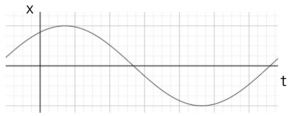
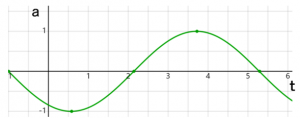
この変位 $x$ が時間 $t$ とともにどのように変化するかをグラフで見てみると、まさに波のように振動している様子がよくわかります。

グラフから読み解く単振動の様子

このグラフの横軸は時間、縦軸は物体の変位（位置）を示しています。時間が進むにつれて、物体が一番右に行ったり、一番左に行ったりと、規則的に揺れ動いているのが見て取れますね。これがまさに「単振動」の姿です。

前回、皆さんにはこの変位の式をもう一度微分して「速度」を、さらに微分して「加速度」の式を導き出すという宿題を出していましたね。今回は、その答え合わせとともに、微積分が単振動の理解にいかに役立つかを見ていきましょう！

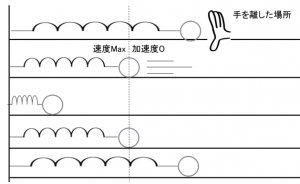
例えば、単振動を始めた物体が振動の中心、つまりバネが自然な長さの位置（原点）を通過する瞬間を考えてみましょう。この時、物体は最も速く動いています。つまり、速度は最大になります。一方で、バネは伸びも縮みもしていないので、物体に働く力はゼロ。ニュートンの運動方程式 $F=ma$ を思い出せば、力がゼロなら加速度もゼロになるはずですよね。

それでは、本当に微積分で導き出される式が、この直感的なイメージと一致するのか、実際に計算して確かめてみましょう。

速度の導出：変位を1回微分！

まず、変位の式 x=Asin(ωt+δ′) を時間 $t$ で1回微分して、速度 $v$ を求めます。

このグラフを見ると、速度も時間とともに波のように変化していることがわかりますね。変位とは少しタイミングがずれていることにも注目してください。

加速度の導出：速度をもう1回微分！

次に、この速度の式 v=Aωcos(ωt+δ′) をさらに時間 $t$ で微分して、加速度 $a$ を求めます。

a=−Aω2sin(ωt+δ′)

となります。加速度も時間とともに変動しているのがわかりますね。しかも、変位のグラフと形は似ていますが、符号が逆になっていることに気づきましたか？

３つのグラフで単振動の全体像を掴む！

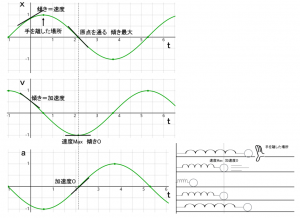
それでは、導き出した変位 $x$、速度 $v$、加速度 $a$ の3つのグラフを時間軸を揃えて並べて見てみましょう。

この図をじっくり見てください。$x-t$ グラフの傾きが速度を、$v-t$ グラフの傾きが加速度を示していることを確認できますね。ここで、先ほど確認した「ボールが振動の中心を通る時」をもう一度見てみましょう。

• $x$ グラフ：原点を通る時なので、$x$ 座標は $0$ ですね。
• $v$ グラフ：この瞬間、速度は負の向きに最大値をとっています。
• $a$ グラフ：そして、加速度は $0$ となっています。

これは、私たちが単振動のイメージとして最初に考えたことと、ぴったり一致していますね！ 微積分で導き出した式が、実際の物理現象を正確に表していることがわかります。

もう一つ、別の瞬間も確かめてみましょう。この図のばねが最も縮んだ瞬間を見てみましょう。

• $x$ グラフ：ばねの縮みが最大、つまり変位が最小（負の最大値）になっています。
• $v$ グラフ：折り返し地点なので、物体は一瞬静止しています。したがって、速度は $0$ となっています。
• $a$ グラフ：ばねが最も縮んでいるということは、物体に働く力も最大です。そのため、加速度も最大値をとっているのがわかりますね。

こちらも、単振動の様子と完全に一致していることが確認できました！このように、微積分を用いることで、単振動における変位、速度、加速度の複雑な関係が、数式としても、そしてグラフとしても、非常にスッキリと理解できます。実際の現象と数式がピタッと一致する瞬間は、本当に面白いですよね！

もちろん、実際の高校入試や定期テストでは、これらの極端な点（振動中心や両端など）における速度や加速度のみが問われることがほとんどで、その間の複雑な場所については微積分を使わない方法で対処することが多いでしょう。しかし、微積分を学ぶことで、なぜそうなるのか、その物理的な背景をより深く理解できることは間違いありません。ぜひ、微積分を物理の強力なツールとして活用してみてください！

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！

３月のイチオシ実験！

• 押し花を作ろう！：梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。

テレビ番組・科学監修等のお知らせ

• 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。
• 2月27日放送予定「チコちゃんに叱られる」（NHK）の科学監修しました。

書籍のお知らせ

• 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
• サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ

• 3/20（金）　日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③　11:20-12:20
• 7/18（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
• 10/10（土）　秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
• 各種SNS　X(Twitter)／instagram／Facebook／BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。