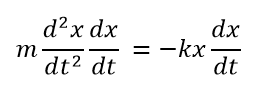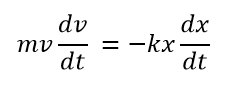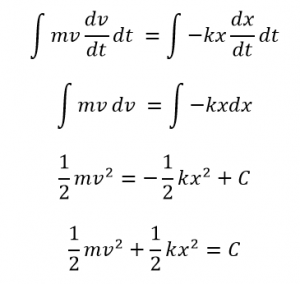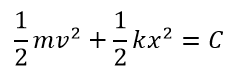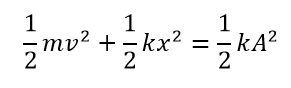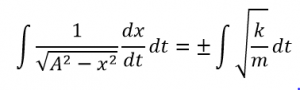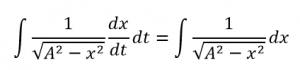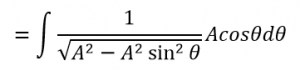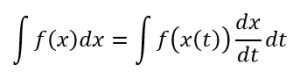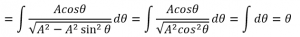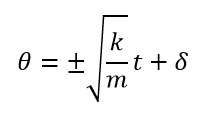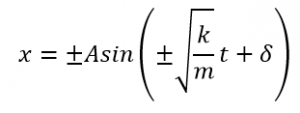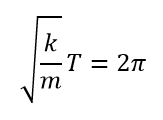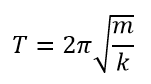高校物理の壁を超える!微積分で迫る単振動の真髄(高校物理と微積分)
サイエンストレーナーの桑子研です。毎日が実験。
今回のテーマは高校物理の中でも、生徒がつまずきやすい「ばねの単振動」です。検定教科書では微積分を使わずに解説されていますが、実は微積分を使うと、その本質がよりクリアに見えてくるんですよ。今回は、その奥深さを一緒に探求し、先生方の授業準備に役立つ具体的な方法や、生徒の「なるほど!」を引き出すヒントをお届けします。
微積分というと、数学の進度を考えると尻込みしてしまう先生もいるかもしれません。しかし、物理現象をより深く理解するためには、微積分は強力なツールになります。今回の記事を通して、単振動の謎を微積分で解き明かし、生徒に「なぜそうなるのか?」を自信を持って説明できるようになりましょう。さあ、一緒にばねの単振動の世界へ飛び込んでみましょう!
ばねの振動の様子を微積で考えてみよう!
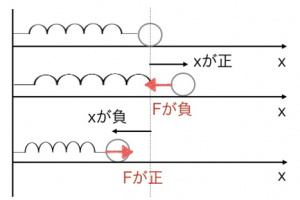
まず、ばねにはたらく力について思い出しましょう。フックの法則から、力 はばねの変位 に比例し、 と表されます。ここでマイナス符号が付くのは、変位 と力の向きが常に逆だからです。例えば、ばねが伸びて が正になると力 は負(縮む向き)に、ばねが縮んで が負になると力 は正(伸びる向き)にはたらきます。
このことか運動方程式は微分表記を使って次のように書くことができます。
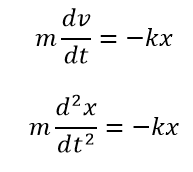
なお速度と加速度の定義式、a=dv/dt, v=dx/dtをつかっています。この微分方程式こそが、ばねの単振動を記述する基本の式となります。
単振動になる理由とは?
それでは、この微分方程式を使って、なぜばねの運動が単振動になるのかを微積分で考えていきましょう。ここからボールの動きについて、なぜ単振動になるのかを微積分を使って考えてみましょう。両辺にdx/dtをかけると次のように表すことができます(これは積分をするための下準備でテクニックだと思ってください)。
ここでdx/dt=v, d2x/dt2=dv/dtなので、
両辺を時間で積分すると、
※Cは積分定数
このようになります。これは力学的エネルギーの保存を示していて、運動エネルギーと弾性エネルギーの和が一定であることを示しています。
運動エネルギー+弾性エネルギー=一定
ここでバネの振幅をAとすると、上記の積分定数Cは1/2kA2と表しても良いですよね。
この式をさらにおしすすめて、ここから変位xの様子について調べてみましょう。
まずは速度vについて常識を展開します。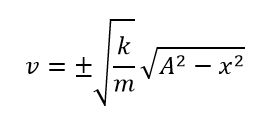
速度vを微分表記dx/dtになおして、変数分離をします。
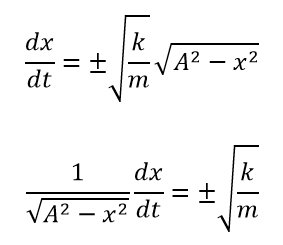
この式の両辺を時間tで積分をします。
このまま眺めていてもうまくいかないのですが、ここで変位xをx=Asinθと置いてみましょう。すると、この微分方程式をとくことができます。
では置いて解いてみましょう。
<左辺>
まず左辺の1/(√A2−x2)の部分は次のようになります。
ここでx=Asinθに置き換えると、
ここでは、次の積分公式を使っています。これらの公式は昨日の記事にまとめましたので、もし公式を忘れてしまったという人は、そちらも御覧ください。
上の式を解いていくと、
となります。
<左辺と右辺を合わせてみる>
右辺と合わせて考えると、
※δは積分定数
となります。このことから、先ほどおいたx=Asinθに代入をすると、
ここでAsin(θ+δ)=Asin(−θ+δ+π)となり、δ+πは定数なので積分定数δ’に入れてしまうことができます。このことから、頭についている±や√の手前についている±を積分定数の中に入れてしまうと、もっと簡単に上の式を表すことができます。
※δ’は積分定数
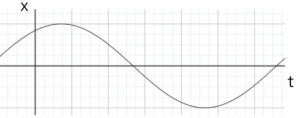
この式を見ると、Aは振幅を、δ’は初期位相を示し、時刻0のときの右辺が初期位置x0となります。この式をグラフにすると、
となります。このようにして単振動となることが示されました。
<周期の公式についても求めてみよう!>
また1回振動するのにかかる時間を周期Tとすると、1周期たつと2πとなることから、
と表すことができます。これを周期Tについて解くと、
となります。単振動の速度は、上記の式を時間で微分すれば、加速度はもう一度微分すれば求めることができます。
いかがでしたでしょうか?学校では微積分を使わない方法で単振動を解きますが、微積分を使って解くと、初期位相が自然に出てきたり、力学的エネルギー保存の法則との繋がりが明確になったり、より深い理解に繋がったのではないでしょうか。
今回の内容を授業で扱う際には、いきなり全ての微積分を見せるのではなく、「なぜ単振動になるのか、もう少し深く考えてみよう」という導入から、段階的に説明していくのがおすすめです。生徒の数学の進度に合わせて、どの部分を重点的に説明するか調整してみてくださいね。
次回は、今回の結果を使って、鉛直につるしたばね振り子や 電気振動(LC回路) など、他の物理現象への応用についても考えていきたいと思います。お楽しみに!
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20

テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日 科学監修をした番組が放送予定です。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。