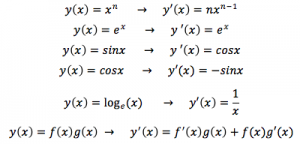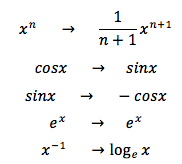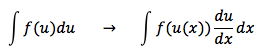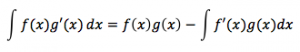【高校物理×微積】これだけは押さえたい!物理で使う微積の基本公式まとめ
サイエンストレーナーの桑子研です。毎日が実験。
現在、物理の現象を「微積分」を使ってスッキリ解釈する方法について、現役生向けに記事を連載しています。高校物理では通常、教科書の構成上、数学Ⅲの内容にあたる微積分は避けられていることが多いのですが、実はこの「微積」を使って考えることで、公式の意味がわかりやすくなったり、複雑な問題がシンプルに見えたりすることがよくあります。
私自身、授業で「この現象、微積を使えば一発で導けるんだけどなぁ…」と思う場面に出くわすことが何度もあります。ただし、数学の教科書には微分積分の公式がたくさん出てきて、生徒や先生も「どれが物理で必要なの?」と迷ってしまうことが少なくありません。
そこで今回は、物理で最低限押さえておきたい微積分の公式を厳選してご紹介します。「これは知っておくと物理がよくわかる!」というものにしぼっていますので、数学に深入りせず、必要なエッセンスだけを身につけていきましょう。
■ 微積を使うと見える!物理の世界
たとえば、次のような場面で微積が登場します。
• 速度と加速度の関係(v = dx/dt, a = dv/dt)
• 力と運動の関係(F = ma)を使った運動方程式の微分方程式化
• 電磁誘導や回路での時間変化(指数関数の登場)
• 仕事とエネルギーの積分計算(W = ∫F dx)
これらの式をスムーズに扱えるようになると、物理の理解度が一段階アップします!
■ 物理でよく使う微積分公式(厳選)
<基本>
<合成関数の微分>
次に積分公式について見て行きましょう。
<基本>
<fがuの関数、uがxの関数の場合>
<2つの関数f(x),g(x)について>
■ 数学の力を借りて、物理を深く理解する
ここで紹介した公式は、ほんの基本中の基本ですが、物理を微積で見直すときの土台になります。
本連載では、これらの公式をどのように使って、どんな現象をスッキリ説明できるのかを、できるだけ数学に立ち入りすぎずに解説していきます。
数学Ⅲの教科書を横に置きながら読んでいただければ、より理解が深まると思いますし、「なんとなく覚えていた公式が、こんなところで役に立つんだ!」という発見がきっとあるはずです。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!
3月のイチオシ実験!
- 押し花を作ろう!:梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。
テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日放送予定「チコちゃんに叱られる」(NHK)の科学監修しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) 秘密兵器「帯電ガン」が炸裂!ビリビリ!ドキドキ!静電気サイエンスショー@千葉市科学フェスタ(午後予定)
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。