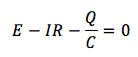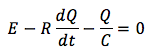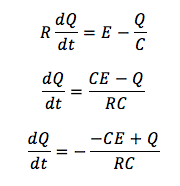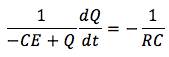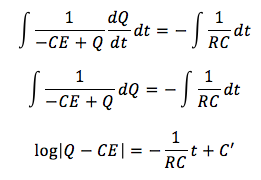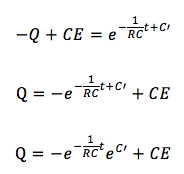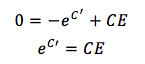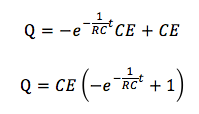高校物理がもっと面白くなる！コンデンサー充電を微積で深掘り（高校物理と微積分）
サイエンストレーナーの桑子研です。毎日が実験。
高校物理の検定教科書では、数学の進度の関係から微分積分を使わずに物理法則が説明されています。しかし、微分積分を用いることで、現象の根底にあるメカニズムがよりクリアに、そしてスッキリと理解できるケースが数多く存在します。今回は、その中でも特に、生徒たちが「なるほど！」と膝を打つような説明ができるようになる「コンデンサーに充電するときの電気量のたまる様子」を、微分積分の視点から掘り下げていきましょう。
前回はコンデンサーの放電について解説しましたが、今回は充電の過程です。放電の様子と比較しながら読み進めることで、電気回路における時間変化の面白さがより一層感じられるはずです。
コンデンサーを充電してみよう！
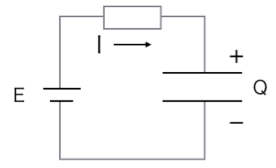
コンデンサーをE[V]の電池で充電する場合について考えてみましょう。
この場合、キルヒホッフの第二法則を使うと、
このように表記できます。微分記号を使って電流を表すと、
となります。ここでコンデンサーにたまる電気量Qは増加するので、dQ/dtは正となります。dQとQに着目をして、変数分離しましょう。
この両辺を時間ｔで積分をすると、
※C’は積分定数
一般解は、
Qははじめ０からスタートするはずなので、CE > Qということが言えます。よって、絶対値をとると、
ここで、時刻t=0のときのコンデンサーの電気量を０[C]とすると、積分定数C’は、
この条件を代入すると、
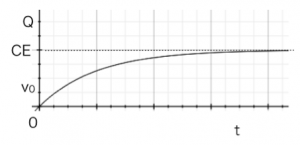
このようにコンデンサーにたまる電気量は表されました。ｔを無限にすると、数式をみてわかるようにQ=CEとなります。これをグラフにしてみましょう。
これがコンデンサーの充電過程の電気量の様子です。
いかがでしたでしょうか。高校物理では、充電された状態や電流を流した直後（）といった特別な時刻の状況はよく問われますが、この間の部分がどのように変化していくのかを、微分積分を用いることで詳細に、そして論理的に考えることができましたね。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
６月のイチオシ実験！
レモンやオレンジで風船を割ろう！インパクトが抜群のリモネン風船の実験
テレビ番組監修・イベント等のお知らせ
- ６月３日（水）20:30〜 「
バカリズムのちょっとバカりハカってみた！」（テレビ東京）を科学監修・出演します。テーマは「 そばの出前は何人前まで運べるのか、限界を測ってみた」です。 - ６月４日(木) 7:00〜 「THE突破ファイル」（日本テレビ）について科学監修しました。
- 6月14日（日） 千葉大学インスタレーション「探究」にて講師を務めます
- 6月26日（金） 公開研究会「脱作業化！デジタル化と段階的指導で実現する オームの法則の探究」
- ６月28日（日） ダビンチマスターズ＠昭和女子
- 7月18日（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
書籍のお知らせ
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
各種SNS（更新情報をお届け！）
X(Twitter)／instagram／Facebook（日本語）
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
