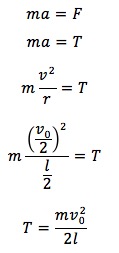視点を変えれば物理は面白い!「重心」と旅する不思議な落下運動の世界【東大物理に挑戦!】(大問1Ⅱ(3)(4))
サイエンストレーナーの桑子研です。毎日が実験。
東大物理2015を解く! 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
「東大の入試問題」と聞くと、「自分には関係ない、難しすぎる世界…」なんて感じていませんか?でも、実はどんなに複雑に見える問題も、シンプルな物理法則の美しい組み合わせでできています。それはまるで、たった数種類のブロックから壮大なお城が作られるようなもの。
前回は、「重心」という魔法のメガネを手に入れ、2つの物体の動きを1つの物語として見る方法を探求しましたね。今回はそのメガネをかけて、さらに一歩踏み込みます。テーマは 「物理法則を使って、無重力空間を体験する方法」 です!
にわかには信じられないかもしれませんが、「視点を変える」だけで、あの重力から解放されたかのような世界が見えてきます。今回挑戦する東大物理2015の大問1のⅡ(3)(4)は、まさにその不思議を体験させてくれる絶好の問題。佐藤雅彦先生の「日常にひそむ数理曲線」の動画で描かれる世界の、まさに核心に迫ります。


[amazonjs asin=”B003MQK8EC” locale=”JP” title=”日常にひそむ数理曲線 DVD-Book”]
※アマゾンのリンク先、画像の左側にある「movie」という文字から、この問題にぴったりの動画を観ることができます。また、代々木ゼミナールのサイト等で問題の原文もぜひご覧ください。
さあ、思考の冒険を始めましょう!
東大物理の目次へ戻る 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
ステップ3:重心と一緒に落下!無重力の世界へようこそ
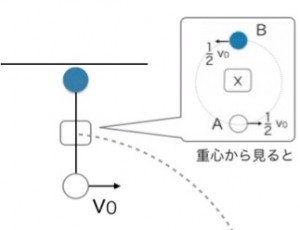
手を離した後の糸の張力はいくらになるでしょう?「(2)と同じかな?」と思うかもしれませんが、状況は全く違います。ではどう考えるか?ここでの鉄則は、やはり「重心に乗り込んで、そこから世界を眺める」ことです。
手を離した後、小球A・B、そしてそのリーダーである重心は、すべて同じ重力加速度 g で落下していきます。想像してみてください。もしエレベーターのワイヤーが切れて自由落下したら、あなたも中の荷物も一緒に落ちるので、お互いの重さを感じなくなり、体がフワッと浮きますよね。これこそが 「無重力」状態です。
それと同じで、重心という乗り物に乗って一緒に落下すると、なんと周りから重力が消えたように見える のです!重心から見ると、AとBは重力の影響を受けず、ただ糸の張力だけで引っぱり合っている状態になります。
この「人工的な無重力空間」では、AとBは重心を中心とした美しい等速円運動を始めます。こうなれば話は簡単。円運動の運動方程式を立てるだけで、張力 T を求めることができます。
ここで(2)で求めた v0=2vを使うと、驚くほどシンプルな答えが出てきます。
T=mg
なんと、張力の大きさは小球1個分の重さに等しいのです。
ステップ4:地上に帰還! それぞれの物体の驚くべき運命
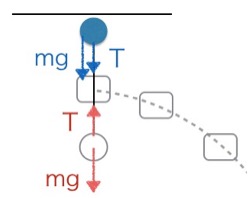
さて、無重力の世界から、再び地上の視点に戻りましょう。それぞれの小球の「本当の」加速度はどうなっているのでしょうか?今度は、AとBそれぞれに働く力をすべて書き出して、運動方程式を立ててみます。下向きを正としましょう。
小球Bの運動方程式
Bには、地球が引く重力 mg と、糸が引く張力 T が、どちらも下向きに働きます。つまり、二つの力でグイグイ下に引っ張られる状態です。(3)で求めた T=mg を代入すると…
Bの運動方程式
ma = T+mg
Tに(3)で求めたmgを代入すると、
ma = 2mg
a = 2g
なんと、通常の自由落下の2倍の加速度!すごい勢いで落ちていくことがわかります。
小球Aの運動方程式
一方、Aには下向きの重力 mg と、上向きの張力 T が働きます。こちらも T=mg を代入すると…。
Aの運動方程式も同様に、
ma= mg−T
ma = 0
a=0
加速度がゼロ!これは驚きです。手を離した瞬間、Aに働く下向きの重力と上向きの張力が完璧に釣り合っているのです。つまり、Aはその瞬間だけ速度が変化せず、まるで時が止まったかのように、それまでの速度を保ったまま運動を続けるのです。
同じ糸で結ばれながら、片や猛スピードで落下し、片やその場で踏みとどまる。視点を変えることで、こんなにもダイナミックで対照的な物語が見えてくるなんて、物理は面白いですね!
東大物理の目次へ戻る 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!