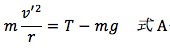東大物理で解き明かす！ジェットコースターが落ちない秘密「円運動」[第1問(2)(3)]
サイエンストレーナーの桑子研です。毎日が実験。
ジェットコースターがぐるんと一回転！逆さまになっても落ちないのは、なぜだか考えたことはありますか？実はその秘密は、今回挑戦する「円運動」という物理現象に隠されています。
「東大の物理」と聞くと難しそうですが、実はジェットコースターや遊園地のコーヒーカップと同じ、身の回りの法則から成り立っています。今回は、東大の入試問題を題材に、スリリングな円運動の世界を解き明かしていきましょう！
東大物理2015を解く！ 第１問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
今回の問題：振り子の円運動
まずは問題を見てみましょう。天井から吊るされたおもりが、ぐるりと運動するお話です。
第１問 (2) 糸にかかる力はどれくらい？
おもりが一番下に来た瞬間、糸にはどれくらいの力がかかっているのでしょうか？これを解くには、物理学の最強タッグ、「運動方程式」と「力学的エネルギー保存の法則」を使います。
ステップ1：力のバランスを考える（運動方程式）
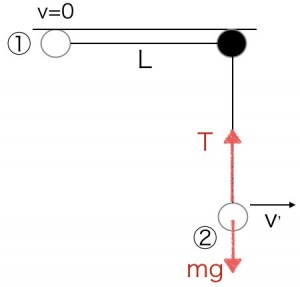
まず、おもりが最下点にいるとき、どんな力が働いているか見てみましょう。
働いているのは、糸がおもりを上に引っ張る「張力 T」と、地球がおもりを下に引く「重力 mg」の2つです。おもりは円運動をしているので、必ず円の中心に向かって引っ張る力、「向心力（こうしんりょく）」が必要です。この問題では、「張力 T」が「重力 mg」に勝った分が、向心力として働きます。
これを運動方程式（力のバランスシート）で表すと、次のようになります。
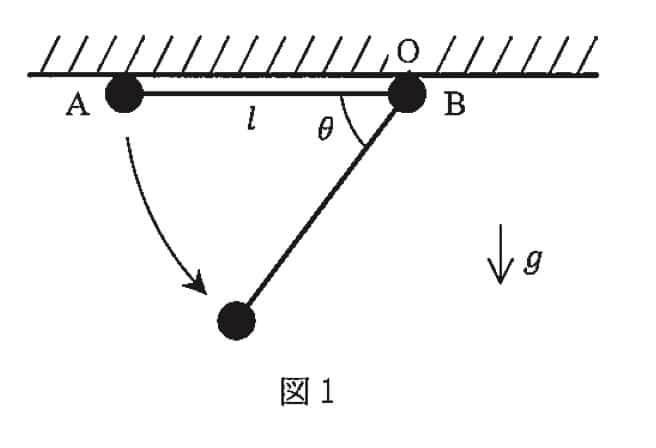
ma = T − mg
この式を「式A」と名付けておきましょう。この式の a（加速度）は、円運動の加速度の公式 a=rv^2を使って、
と書き換えられます。張力Tを求めるには、最下点での速さv’が分かれば良さそうですね。
ステップ2：エネルギーの変化を追う（エネルギー保存則）
次に、速さv’を求めるために、エネルギーに注目します。一番高い位置（①）から一番低い位置（②）に移動するとき、エネルギーはどのように変化するでしょうか？
①（最高点）のエネルギー：速さは0なので、運動エネルギーは0。高さLの位置エネルギー mgL だけを持っています。
②（最下点）のエネルギー：高さを基準（0）とすると、位置エネルギーは0。速さv’の運動エネルギー1/2mv’^2だけを持っています。
（①のエネルギー）＝（②のエネルギー）
この「エネルギー保存の法則」から速さv’を計算すると、v’=2gLとなります。
ステップ3：合体させて答えを出す！
さあ、いよいよ大詰めです。ステップ2で求めた速さv’を、ステップ1で作った「式A」に代入します。
これをTについて解くと、T = 3mg という答えが出てきます。
この問題のポイント！
この問題の面白いところは、答えが「3mg」になる点です。これは、おもりがただぶら下がっている時（張力はmg）の3倍もの力が糸にかかっていることを意味します！ブランコを漕いでいて、一番下に来た時にぐっとお尻が椅子に押し付けられる感覚、あれがまさにこの力の正体です。
このように、「運動方程式」と「エネルギー保存則」を組み合わせるのは、円運動の問題を解くための王道パターン。ジェットコースターのループなど、身の回りの多くの現象もこの組み合わせで説明できるのです。
(3) 最下点での加速度は？
この問題は(2)が解ければボーナス問題です！円運動の加速度の公式 a=rv^2に、先ほど求めた最下点での速さ v’=2gLを代入するだけ。
答えは 2g となります。地球の重力加速度の2倍の加速度で、おもりは向きを変え続けているのですね。
東大物理2015を解く！ 第１問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
４月のイチオシ実験！
- 光の魔法CMYウォーターキューブ：光の魔法を体験せよ！水を注ぐと新たな立方体が出現する魔法のような実験です。
テレビ番組・科学監修等のお知らせ
- 4月9日（木）「THE突破ファイル」（日本テレビ ）の科学監修を行いました。夜7時〜となります。
書籍のお知らせ
- サクセス15 ４月号にて、野球の科学について記事を執筆しました（2026/3）
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
講師・ショー・研究等のお知らせ
- 3/20（金） 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表しました。
- 6/14（日） 千葉大学インスタレーション「探究」にて講師を務めます
- 7/18（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10（土） 秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
- 各種SNS X(Twitter)／instagram／Facebook／BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
- 数万の価値が無料に！？数式グラフ化の神アプリ「Desmos」で視る電気の丘
- 鼻歌まじりの決死圏？月面ジャンプに隠された「真空と重力」の驚きのストーリー（アポロ計画）
- 見えない電位を立体で捉える！ランチボックスの蓋で作る驚きの科学工作
- 影が教える物理の秘密！等速円運動と単振動の意外な関係（単振動と等速円運動のつながり）
- 見えない「力」をデジタルで可視化！最新型ばねばかりが理科の常識を変える
- 「ようこ」と一緒に原子核の旅へ！物理学者・多田将が描く、世界一わかりやすい核の正体
- 【科学監修】教科書は「魔法の書」だった？深夜番組で解き明かす日常の科学「教科書で習ったアレ」（テレビ朝日）
- 時間が「色」で見える？集中力を引き出す魔法の道具・タイムタイマーからPretty Progressまで
- ガッチャンコで速度が半分に？2台の台車で挑む、衝突と合体の運動量実験
