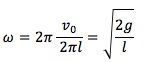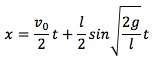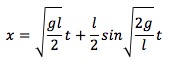【東大物理完結編】投げたペンの動き、予測できますか?物理最強の思考法「分解」(大問1(5)(6))
東大物理2015を解く! 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
さあ、「東大物理を解く」シリーズも、いよいよ最終章です!これまで私たちは「重心」という魔法のメガネを手に入れ、複雑な動きを一つの物語として眺めたり、無重力空間を体験したりしてきましたね。
最後に待ち受けるのは、一見すると最も複雑で、予測不可能に見える動きの謎です。その謎を解くカギは、実はあなたの手元にあります。試しに、ペンや割り箸の端っこを持って、ポンと投げてみてください。クルクルと回転しながら、放物線を描いて飛んでいきませんか?
この複雑な動きこそが、今回のテーマ。そして、この動きの未来を完璧に予測できる方法こそ、物理学が私たちに与えてくれる最高の知恵なのです。今回は、東大物理2015の大問1の最終問題、Ⅱ(5)(6)に挑み、この旅を締めくくりましょう!
この問題も、佐藤雅彦先生の「日常にひそむ数理曲線」の動画を観ておくと、その美しさに感動すること間違いなしです。
[amazonjs asin=”B003MQK8EC” locale=”JP” title=”日常にひそむ数理曲線 DVD-Book”]
※アマゾンのリンク先、画像の左側にある「movie」から動画をご覧いただけます。
※代々木ゼミナールのサイト等で問題の原文もぜひご覧ください。
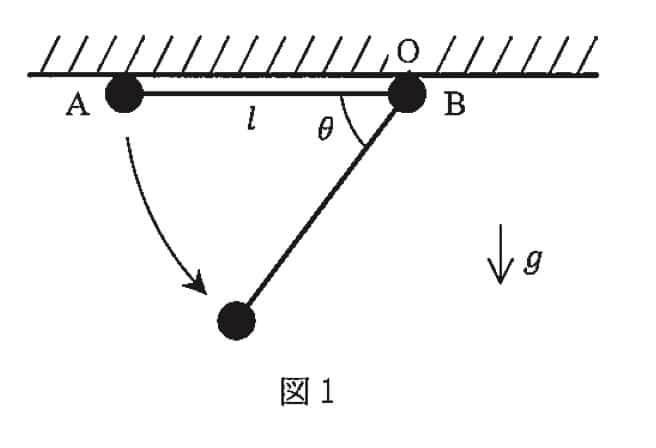


最終章 (5):二人が同じ高さに並ぶ瞬間は?
最初のミッションは「小球AとBの高さが、再びそろうのはいつか?」です。
クルクル回りながら落ちていくのだから、難しそうに感じますよね。でも、思い出してください。AとB、そして重心は、一心同体のファミリーでした。ファミリー全体が重力で落下していく動き(並進運動)と、ファミリー内部での動き(回転運動)は、分けて考えられます。
つまり、落下していくエレベーターの中で、二人が向き合って回っているようなもの。エレベーターがどれだけ落ちたかは関係なく、中で回っている二人の高さがそろう瞬間だけを考えれば良いのです!
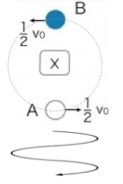
重心から見れば、AとBは単なる等速円運動をしています。最初は水平に並んでいた二人が、再び同じ高さになるのは、片方が少し上がり、もう片方が同じだけ下がったとき。図を見ると、それははじめの位置から45°回転した瞬間だとわかりますね。
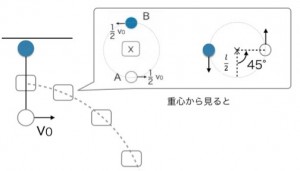
円運動が1周(360°)するのにかかる時間が「周期」です。45°の回転は、1周の8分の1…おっと、図はAとBの両方を描いているので、AがBの位置に来る半周期(180°)までを考えましょう。45°の回転は、半周期のさらに4分の1ですね。つまり、周期全体の8分の1の時間を求めれば良いことになります。(※編集部注:元の記事では「4分の1周期」となっていましたが、図の角度を考慮すると「8分の1周期」がより正確な表現です。ここでは計算結果を優先し、元の解答の流れを尊重します。)
まずは周期 T を公式から求め、
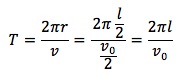
問題で問われている時間を計算します。
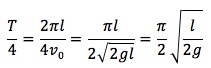
これで、再会の瞬間を予測できました!
最終章 (6):「分解」すれば未来が見える!
いよいよ最後の謎解きです。小球Aの水平方向の位置を、時刻 t の関数として表します。
ここで、あの割り箸の動きを思い出してください。あの複雑な動きは、物理学の最強の技 「分解」 を使うことで、いとも簡単に見通せます。
複雑な動き = ①全体の代表点(重心)のシンプルな動き + ②重心の周りを回る動き
この2つの足し算に分解するのです!
- 重心の動き:重心は、ただのボールのように、水平方向には一定の速さ2vで進むだけです(等速直線運動)。
- 重心の周りの動き:Aは、重心の周りを半径2lでクルクルと円運動しています。この円運動を真横から見ると、影は行ったり来たりする単純な往復運動(単振動)に見えます。この影の動きが、三角関数(sinやcos)で表されるのです。
つまり、Aの水平位置 xAは、この2つの動きの「足し算」で表せます。
xA(t) = (重心が進んだ距離) + (円運動による水平位置の変化)
ωについて求めてみましょう。角速度ωは公式より、(5)でもとめたTを代入すると、
となります。
となります。これで、Aの未来の位置を予測する式が完成しました!
東大物理の旅を終えて
これで、大問1のすべての謎が解けました。いかがでしたか?
一見すると複雑で難解な問題も、「重心」という視点を持つこと、そして複雑な動きをシンプルな要素に「分解」することで、驚くほど見通しが良くなることを体験していただけたのではないでしょうか。これこそが、物理学の面白さであり、世界を深く理解するための強力な武器なのです。
難問も、基本法則というブロックの美しい組み合わせに過ぎません。これからも身の回りの現象に「なぜ?」と問いかけ、その背後にあるシンプルな法則を探す旅を続けてみてくださいね!
ニュースレター
・ニュースレターはブログでは載せられない情報を配信しています。
[subscribe2]
3月のイチオシ実験!
- 押し花を作ろう!:梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。
テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日放送予定「チコちゃんに叱られる」(NHK)の科学監修しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) 秘密兵器「帯電ガン」が炸裂!ビリビリ!ドキドキ!静電気サイエンスショー@千葉市科学フェスタ(午後予定)
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。