物理が苦手な人へ。東大の問題を題材に「エネルギー保存則」を完璧に理解しよう（東大物理を解く！[第1問(1)]）

サイエンストレーナーの桑子研です。毎日が実験。

「東大の入試問題」と聞くと、なんだかとても難しそうで、自分には関係ない世界の話…なんて思っていませんか？でも、実はどんなに難しい問題も、基本となるシンプルな法則の組み合わせでできています。今回は、あの東京大学の物理の入試問題を使って、一見複雑に見える問題を「たった3つのステップ」で解き明かす方法をご紹介します。この考え方は、物理の冒険に出るための強力な羅針盤になりますよ！

2015年 東京大学 物理 第1問に挑戦！

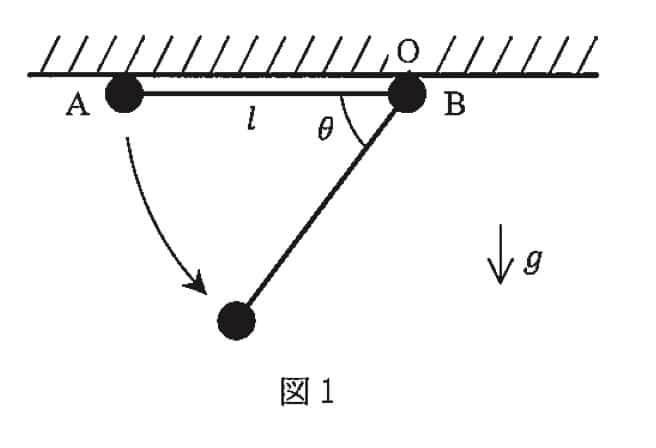
今回挑戦するのは、2015年の東京大学で実際に出題された問題です。振り子が揺れる、というシンプルな設定ですね。

それでは、この問題を解くための最強ツール、「3ステップ解法」を使って解説していきます！

第１問 Ⅰ（１）の解説

この問題は、振り子Aの動きに注目する問題です。このような運動を考えるとき、物理学で非常に重要な「力学的エネルギー保存の法則」という考え方を使います。これは、「摩擦や空気抵抗などがなければ、位置エネルギーと運動エネルギーの合計は常に一定に保たれる」という法則です。

ブランコで遊ぶときを想像してみてください。一番高いところでは一瞬止まり（運動エネルギー０、位置エネルギー最大）、一番低いところでは最も速く（運動エネルギー最大、位置エネルギー最小）なりますよね。このように、エネルギーは姿を変えるだけで、全体の量は変わらないのです。

この法則を使いこなすための手順が、「3ステップ解法」です。

１　前①後②の絵を書く
２　①②の力学的エネルギーを書き出す
３　仕事も考えて、エネルギー保存の式を作る

では、ステップごとに見ていきましょう。

ステップ１：前①後②の絵を書く

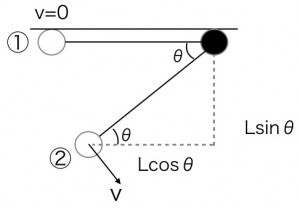
まず、物理現象を「変化の前（Before）」と「変化の後（After）」の２つの場面に分けて、簡単な絵で表します。今回は、振り子が一番高い位置にあるときを「前①」、角度がθになった瞬間を「後②」とします。

絵を描くことで、状況が整理され、考えやすくなります。この図から、②の高さは、①の位置に比べてどれだけ低いかがわかりますか？図の中に直角三角形を見つけると、Lsinθ だけ低いことがわかります。これが位置エネルギーを計算するカギになります。

ステップ２：①②の力学的エネルギーを書き出す

次に、①と②のそれぞれの場面での力学的エネルギーを式で表します。一番低い②の高さを基準（0）としましょう。

①の力学的エネルギー：一番高い位置なので、速さは0です。つまり運動エネルギーは0。位置エネルギーだけで、その値は mg(Lsinθ) となります。

②の力学的エネルギー：基準の高さなので、位置エネルギーは0です。速さを v とすると、運動エネルギーはとなります。

ステップ３：エネルギー保存の式を作る

最後に、①と②のエネルギーが等しいという式を作ります。このとき、外部から力が加わって「仕事」をされていないかチェックします。今回は、糸の張力が働いていますが、張力は常に振り子の進行方向と垂直なので、仕事をしません。つまり、外部からの仕事は0です。

したがって、エネルギー保存の法則がそのまま成り立ちます。

mg(Lsinθ)+0=1/2mv^2

（①の力学的エネルギー）＋（仕事）＝（②の力学的エネルギー）

この式を v について解くと、答えが導き出せます。

この問題のポイント！

どうでしたか？一見難しそうな東大の問題も、実はブランコと同じ「エネルギー保存の法則」を使う基本的な問題だったのです。ポイントは、図を描いて直角三角形を見つけ、正確に高さを求めること。これは大学入試共通テストなどでも頻出の、非常に重要な考え方です。

難しい問題も、基本に立ち返って一つずつステップを踏めば必ず解ける。それが物理の面白さです！

東大物理2015を解く！ 第１問Ⅰ(1)、(2)(3)、Ⅱ(1)(2)　(3)(4)　(5)(6)

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！

３月のイチオシ実験！

• 押し花を作ろう！：梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。

テレビ番組・科学監修等のお知らせ

• 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。
• 2月27日放送予定「チコちゃんに叱られる」（NHK）の科学監修しました。

書籍のお知らせ

• 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
• サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ

• 3/20（金）　日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③　11:20-12:20
• 7/18（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
• 10/10（土）　秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
• 各種SNS　X(Twitter)／instagram／Facebook／BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。