プログラミングで探る！ウサギとクマの不思議な「生物のつり合い」（Scratch）
サイエンストレーナーの桑子研です。毎日が実験。
食物連鎖って、学校で習いましたよね？ 草を食べるウサギがいて、そのウサギをクマが食べる…。「ピラミッド構造になる」と教科書には書いてあるけれど、本当にそうなるのか、不思議に思ったことはありませんか？
このピラミッドの頂点にいる生き物は数が少なく、底辺にいる生き物は数が多くなります。これはなぜでしょう？
実は、ピラミッドの形は、単に「強い者が上にいる」という話ではなく、地球のエネルギーのめぐりと深く関係しているのです。エネルギーは、生き物が別の生き物に食べられるたびに、その多くが失われていきます。
たとえば、草が太陽の光エネルギーを使って育ちます。この時、草が作ったエネルギーは、ウサギに食べられるとすべてウサギに移るわけではありません。ウサギの体温を保ったり、動いたりするためにエネルギーが使われるので、ウサギの体になるエネルギーはごく一部です。クマがウサギを食べるときも同じことが起こります。そのため、上位に行くほど、生きられる個体の数がどんどん少なくなっていくのです。
🔬 身近な科学！「生物のつり合い」をプログラミングでシミュレーション
私たちが住む地球は、実は「生物のつり合い」という不思議なバランスで保たれています。もし、ある生き物だけが増えすぎたり、減りすぎたりしたらどうなるでしょう？
それを確かめるために、簡単なシミュレーションプログラムを作ってみました。登場するのは、草（生産者）、ウサギ（第一次消費者）、 クマ（第二次消費者） の3種類です。
#食物連鎖 の単元について、ピラミッド構造になるのかどうか？というのを単純な #実験 を #Scratch でプログラムで組んでみました。登場するのは、草（ #生産者 ) 、うさぎ( #第一次消費者 )、熊( #第二次消費者 )の３つで（カッコ内は設定）、うさぎは草を食べ、熊はうさぎを食べるという関係にあります。１年を考えて、草を食べたうさぎは○がつき、うさぎをたべた熊は○がつきます。
https://scratch.mit.edu/projects/622018092
このプログラムでは、それぞれの生き物の数が時間とともにどう変化していくかを観察できます。
🐇 ウサギとヤマネコの不思議な関係
実際に自然界でも、この生物の数の変動は観察されています。たとえば、カナダのツンドラ地帯に住むカンジキウサギと、それを食べるカナダオオヤマネコの関係です。
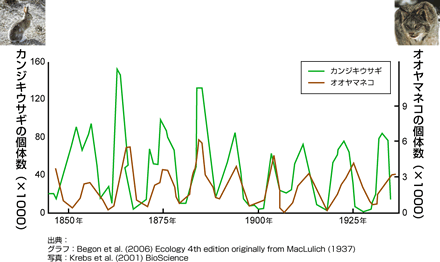
生命試研究館 引用：https://www.brh.co.jp/publication/journal/064/research_1（2021-12-31）
グラフを見るとわかるように、ウサギが増えると、それを食べるヤマネコも増えます。しかし、ヤマネコが増えすぎるとウサギが減り、今度は食べ物がなくなったヤマネコも減っていきます。すると、ウサギを食べる天敵が減るので、またウサギが増え始める…。このように、まるで波のように数が増えたり減ったりを繰り返しながら、全体のバランスが保たれているのです。
この現象は「捕食-被食関係」と呼ばれ、生物学の世界ではとても有名な話です。この複雑な関係を、今回のプログラムでは単純なルールで再現しています。
📈 シミュレーションで「ピラミッド」の謎に迫る
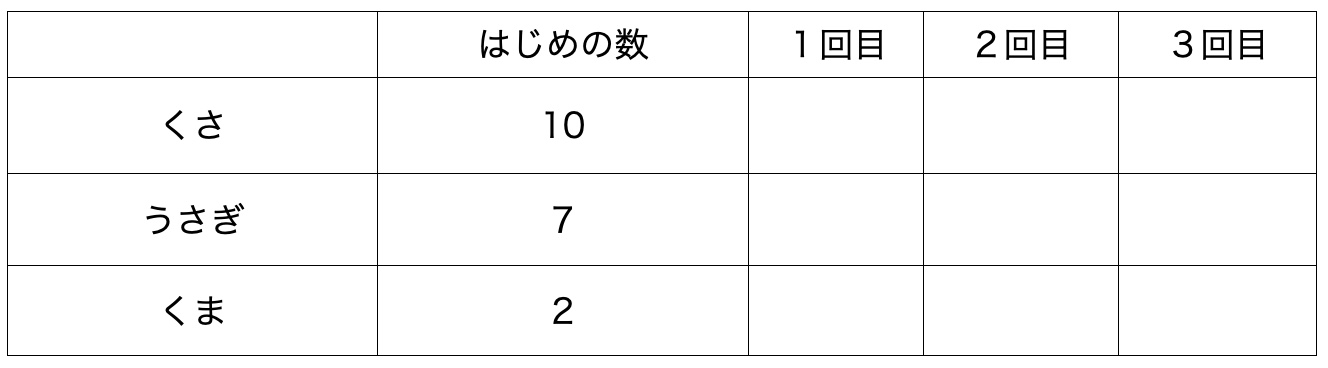
今回のプログラムでは、はじめにそれぞれの生き物の数を自由に設定できます。
たとえば、草10、ウサギ10、クマ10という、ピラミッドとはかけ離れた状態でスタートしてみましょう。
https://scratch.mit.edu/projects/622018092
草が10本しかないのに、ウサギとクマがそれぞれ10匹もいたらどうなるでしょう？
すぐに食べ物が足りなくなり、ウサギは草を食べられず死んでしまいます。そして、ウサギが減ったことで、クマも飢えてしまいます。結果として、ウサギもクマも激減するでしょう。
実際にプログラムを動かしてみると、ウサギとクマの数が大きく変動した後、やがてある程度の数に落ち着いていく様子が観察できます。この最終的に落ち着いた数が、その環境で生きられる 「生物のつり合い」 なのです。そして、その時の個体数は、生産者である草が一番多く、次がウサギ、一番少ないのがクマ、というピラミッドの形に近づくはずです。
別のスタート数でも試してみよう！
プログラムのステージでは、変数を変えてスタート数を調整できます。
草10、ウサギ3、クマ10
https://scratch.mit.edu/projects/622527162
草3、ウサギ10、クマ10
https://scratch.mit.edu/projects/622522848
草10、ウサギ10、クマ3
https://scratch.mit.edu/projects/622527653
これらのシミュレーションを何度も繰り返してみると、同じスタート数でも、生き物の動きや位置がランダムなため、毎回違う結果になることがわかります。しかし、最終的には特定のバランスに落ち着くことが多いはずです。
これは、自然界の予測不可能性を反映していると同時に、それでも 「生物のつり合い」 という大きな法則が働くことを示しています。
生物の数がどのように決まり、そして変動していくのか。皆さんもこのプログラムを使って、自分なりの予測を立てて、実験してみてください。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
３月のイチオシ実験！
- 押し花を作ろう！：梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。
テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。
- 2月27日放送予定「チコちゃんに叱られる」（NHK）の科学監修しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
- サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
講師・ショー・その他お知らせ
- 3/20（金） 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③ 11:20-12:20
- 7/18（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10（土） 秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
- 各種SNS X(Twitter)／instagram／Facebook／BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
