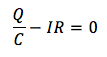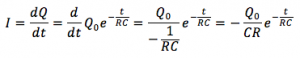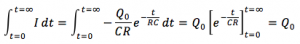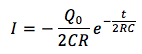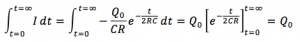微積分でスッキリ!コンデンサーの電気のたまり方を深掘り(高校物理と微積分)
サイエンストレーナーの桑子研です。毎日が実験。
高校物理の「なぜ?」を深掘り!微積分でスッキリわかるコンデンサーの電気のたまり方

こんにちは、理科教師の皆さん!日々の授業、お疲れ様です。高校物理の教科書では、数学の進度を考慮して微積分を使わずに説明がなされている単元が多くありますよね。しかし、中には「ここで微積分を使えば、もっと本質が見えてくるのに!」と感じる現象も少なくないのではないでしょうか。
このブログでは、そんなモヤモヤをスッキリさせるべく、微積分を用いることで理解が深まる高校物理のトピックを深掘りしていきます。今回は、多くの先生方が授業で扱われるであろう コンデンサーの電気のたまり方 について、微積分を使って考えてみましょう。この内容は、生徒に直接教える機会は少ないかもしれませんが、先生方の深い理解が、きっと授業の質を高めることに繋がります。
未知のコンデンサーの電気容量を電流から探る!
皆さんは、未知のコンデンサーの電気容量を調べる際、どのような方法を思い浮かべるでしょうか? 実は、微積分を用いると、コンデンサーの放電時の電流変化から、その電気容量を導き出すことができます。
具体的な手順としては、まずコンデンサーを充電し、その後放電させながら、各時間でどれだけの電流が流れたかを測定します。そして、その電流値に測定間隔の時間をかけて足し合わせること( 積分 すること)によって、コンデンサーに蓄えられていた電気量を求め、おおよその電気容量を調べることが可能になるのです。
こちらの実験もぜひ参考にしてみてください。
なぜこのような方法で電気容量がわかるのか、今回はその背後にある物理法則と微積分の力を紐解いていきましょう。

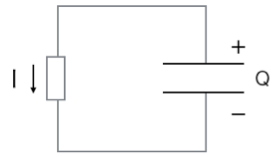
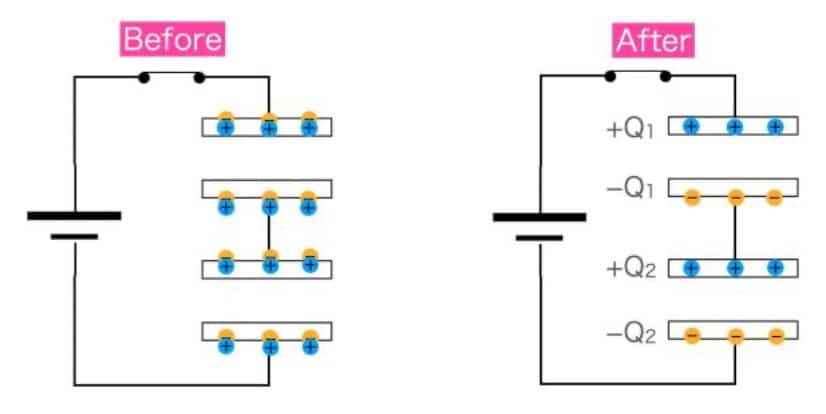
まず次の図のように、コンデンサーに電荷をある電圧Vでためたあとに、放電させた様子を考えてみましょう。
コンデンサーの両端の電圧をV、抵抗の大きさをRとすると、キルヒホッフの第二法則から、
![]()
となります。コンデンサーの電気容量をC、あるときのコンデンサーにたまっていた電気量をQとすると、Q=CVより、
となります。ここで電流の定義式I=dQ/dtを使います。抵抗に流れる電流は減少をしていることに注意をすると、このときの電流はコンデンサーから回路に流れた電流dQを使って、I=−dQ/dtとなります(マイナスがつくのは、減少をしているため)。
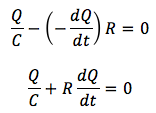
R、Cは定数なので、変数分離を行うと、
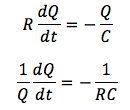
時間tで積分をすると、
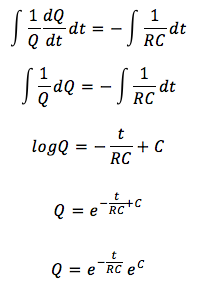
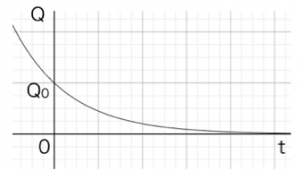
Cは積分定数です。時刻0のとき、つまり初期状態でコンデンサーに電気量がQ0たまっていたとすると、積分定数eCはQ0となります。よって、
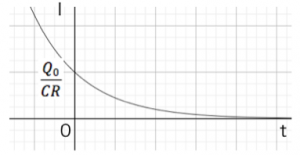
となります。この様子をグラフにすると、
これがコンデンサーにたまった電気量が減っていく様子です。電気量Qを直接測ることは難しいので、このときの電流変化を求めてみましょう。電流の定義式から、電気量の式を時間で微分してみましょう。
電流の大きさのみをグラフにすると、
ここで電流が囲む面積、t=0からt=∞まで積分して、求めてみます。
このことからもわかるように、各時間に流れた電流と、測定時間とで囲まれた面積を積み上げていくと、コンデンサーにたまっていた電気量Q0を求めることができることがわかりました。充電していたときの電圧V0を使えば、Q0=CV0からコンデンサーの電気容量を求めることができるというわけです。
実際に実験をやると、入れる抵抗によっては、電荷の放出時間が短すぎて、電流値の測定が困難なときがあります。そのようなときには抵抗値の大きさを大きくしてみると、放出時間が長くなります。数式をつかってたしかめてみましょう。例えば抵抗値Rの大きさを例えば2倍にしてみると、流れた電流の大きさは、
グラフをかいて、Rの場合と2Rの場合を比較してみましょう。
2Rの場合のほうが、変化がゆるやかになり、長い時間をかけて放出することがわかりますね。このため実験をしたときに電流を測りやすくなります。このときの面積は当たり前ですが、充電した量は変えていないので、先ほどの面積と同じQ0になっているはずです。計算をしてみましょう。
同じになりました(^^)。
以上、微積分を使ったコンデンサーの電気量の変化のお話でした。
高校物理では、コンデンサーの充電や放電の「前後」の状態は扱われますが、その「途中」の変化を微積分で追うことはなかなかありません。しかし、このように微積分を用いることで、コンデンサーの電気量の変化や電流の変化がどのような法則に従っているのかがスッキリと理解できます。
動画による解説について
コンデンサーについて動画で解説しました。プリントをダウンロードしてご覧ください。
3章 コンデンサー
|
小学生のころにさわったことのある素子が再び登場!コンデンサーの性質とそれを組み込んだ回路について学びます。 |

|
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20
 体中に梱包材をはりつけてみよう!
体中に梱包材をはりつけてみよう!
テレビ番組等・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師等・ショー・その他お知らせ
- 2/20(金)「生徒の進学希望実現支援事業」研究授業@福井県立若狭高等学校 講師
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。