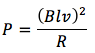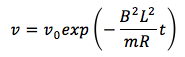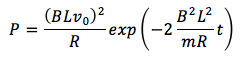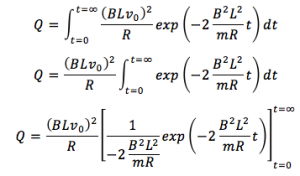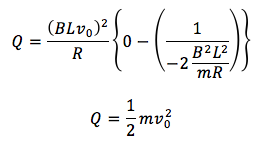微積でスッキリ！電磁誘導で発生した熱は一体どこからやってくるの？

サイエンストレーナーの桑子研です。毎日が実験。

微積でスッキリ解ける！物理のジュール熱を“積分”で考えてみよう

高校物理では「微積を使わないで説明する」という方針のもと、教科書がつくられています。これは数学の進度の関係もあり、生徒が“まだ積分を習っていない”ことが前提になっているからですね。でも、物理って実は「微積があればもっとわかりやすい」と感じる場面がたくさんあるんです。

このコーナーでは、「微積を使うと理解しやすい！」そんな物理の場面を一つずつ掘り下げていこうと思います。

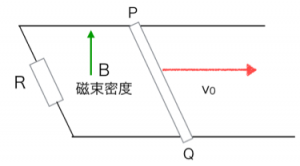
今回は前回求めたコの字型回路で、速度が初速度v₀から止まる(v=0)になるまでに、

　電流が回路に流れることによって、抵抗から発生するジュール熱がどこからやってきたのかについて考えてみましょう。

■ ジュール熱はどこから？

まず、考えてほしいのはこれ。

「回路に流れる電流によって発生したジュール熱って、一体どこからやって来たの？」

高校物理の教科書では、エネルギー保存の視点からこの問題を解きます。でも今回は、微積を用いて“積分で求めてみる”ことにチャレンジしてみましょう。

■ 微積でジュール熱を求めるプロセス

ジュール熱Qは、電力×時間で求められます。

Q = Pt

ジュール熱Q＝電力×時間

ここで、P（電力）は時間とともに変化するので、積分が必要になります。

ただし今回の場合は、電力P自体も変化していきますので、時間で積分をする必要がでてきます。電力P＝IVについては、IとVはコの字型回路の場合、どちらも変化していくので、一定のものである抵抗値Rで置き換えを行います（オームの法則V=IR）。

P=RI²

　コの字型回路に流れる電流はI=Blv/Rなので、

　となります。ここで、前回のある時刻の速度は次の式で示されるので、

　これを先ほどの式に代入すると、

　これを時刻０から時刻∞まで積み上げて積分をすれば、熱量Qを求めることができます。計算をしてみましょう。

　ここで、y=e^−xについて、ｘを∞にするとｙ＝0、またｘを０にするとｙ＝１になるので、同様に考えれば、

「微積って難しそう…」という生徒も、こうして“意味のある使い方”を経験することで、少しずつ慣れていきます。今回は0から∞まで積分しましたが、「ある時刻tまでの熱量は？」という問いにしてみると、さらに広がりますね。このシリーズでは、他の物理項目もどんどん微積でスッキリさせていきます。どうぞお楽しみに！

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！

５月のイチオシ実験！

キーンと冷えるドライアイス！気温が上がってくるこの時期・ドライアイスを使った昇華・凝結・等速度直線運動の実験はいかが？

液体ゼロ！ドライアイスが消えるまでの３時間を科学する（昇華・凝結・等速度直線運動）

テレビ番組監修・イベント等のお知らせ

• 4月30日（木）「THE突破ファイル」（日本テレビ）の科学監修を担当しました。
• 5月8日（金）理科教育ニュースを担当しました。
• 6月14日（日）　千葉大学インスタレーション「探究」にて講師を務めます
• 6月26日（金）　千葉大学の公開研究会（中学理科について授業公開予定）
• 7月18日（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。

書籍のお知らせ

• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
  
  
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
  

各種SNS（更新情報をお届け！）

X(Twitter)／instagram／Facebook（日本語）

BlueSky／Threads（英語）

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。