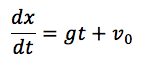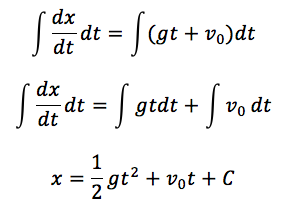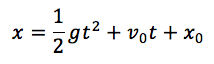物体はどう落ちる？ 微積でスパッと理解する落下の法則！（物理と微積 第２回）
サイエンストレーナーの桑子研です。このサイトで科学を一緒に楽しみましょう。
前回は、力が働かない場合の運動についてお話ししましたが、今回は「力が働く場合」、特に「落下運動」について、微積分を使って解説していきます。
落下運動と微積分
私たちが日常で目にする「落下運動」は、重力という一定の力が物体に働くことで起こります。地球上では、重力加速度（ g ）はほぼ一定で、約9.8 m/s²です。この重力が物体にどのような影響を与えるのか、微積分を使って見ていきましょう。
1. 速度の導出
まず、物体に働く力（重力）を考えます。質量を m とすると、重力による力は mg です。この力が物体に加速度を与えます。ニュートンの運動方程式（ F = ma ）より、加速度 a は次のようになります。
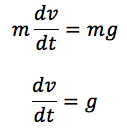
この式の両辺を時間 t で積分すると、速度 v が求められます。
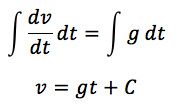
※Cは積分定数
ここで、積分定数 C は初期条件によって決まります。例えば、時刻 t = 0 での速度を v0とすると、C=v0となり、
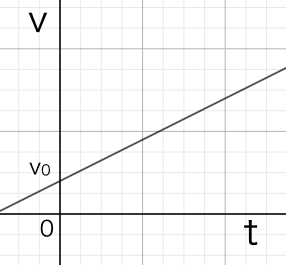
つまり、物体の速度は時間とともに直線的に増加します。前回の等速度運動の式と比べると、速度が時間ｔの増加とともに、増えていくのがわかりますね。グラフにすると次のような感じになります。
このグラフの傾きは、重力加速度ｇとなります。
2. 位置の導出
次に、位置（変位） x を求めてみましょう。速度 v は位置の時間微分なので、
この式の両辺を時間 t で積分すると、位置 x が得られます。
※ Cは積分定数
時刻０のときの位置をx0とすると、C＝x0となります。このことから上の式は次のように書くことができます。
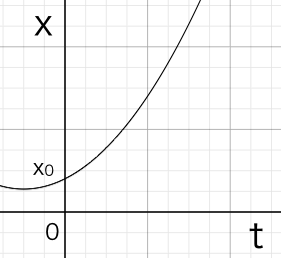
この式は、物体の位置が時間の二次関数として変化することを示しています。つまり、時間が経つにつれて、物体は加速度的に移動距離を増やしていくのです。グラフにしてみると、次のようになります。
微積分を用いることで、力が働く運動、特に重力下での落下運動をより深く理解することができます。速度が時間に対して直線的に増加し、位置が時間の二次関数として変化することがわかりました。次回は、さらに複雑な運動について見ていきましょう。
なお、このように運動方程式から速度や位置を求める手法を「運動方程式を解く」といいます。微積分を活用することで、物理現象をよりシンプルに理解できるので、ぜひ挑戦してみてください！
科学のタネを発信中！
NEW 7/21（火）発売！ 分解問題集
- ７月２１日（火）発売 『高校入試 分解問題集 理科』（学研）…難しい問題も小さな問題に分解することで、問題を解くことができます。そんな分解の技術が身につくように深く関わりを持って作りました。
７月のイチオシ実験！
夏でプシュッと爽やか実験！
テレビ番組監修・イベント等のお知らせ
- ７月１８日（土）「TIF presents ONE SONG FES. 」（フジテレビ）
- 7月18日（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」
- ７月３０日（水） 監修したテレビ番組放送予定
- 12月26日（土） ナリカサイエンスアカデミー（教員向け実験講習会）開催
書籍のお知らせ
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
各種SNS（更新情報をお届け！）
【日本語】X(Twitter)／instagram／Facebook 【英語】BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
