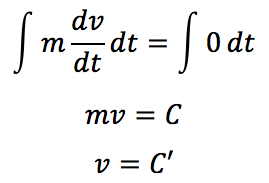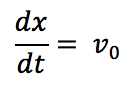「微積なんていらない？」いや、むしろ使ったほうが簡単です！（物理と微積 第1回）

サイエンストレーナーの桑子研です。このサイトで科学を一緒に楽しみましょう。

高校物理と微分積分──力と運動の関係を考える

高校の物理では、基本的に 微分積分（微積）を使わず に学習を進めます。これは数学の進度と合わせるためですが、実は微積を使ったほうがスッキリと理解できる部分も多いのです。

今回は、「力と運動の関係」に注目しながら、微積を使うことでどのように理解が深まるのかを見ていきましょう。

等速度運動と微積分

力が働かないときの運動

まずは 力がまったく働かない場合 を考えてみましょう。例えばカーリングのストーンが動いている様子などです。

高校物理では、このとき物体は「等速直線運動をする」と学びます。運動方程式から、

　力がはたらかないので、右辺は０です。

　加速度を微分を含む式で表記をすると、

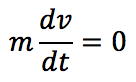
これをｔで積分をすると、速度ｖは次のようになります。

※　Cは積分定定数。C’はm/Cが一定なのでC’とおいている。

　時刻０のときの速さをv₀とすると

　となります。よってv=v₀となり、力がはたらかない場合、物体は等速度運動をすることが示されましたね。

等速度運動と距離の式

v=v₀を微分を含む式で表記すると、

　先ほど同様に、時間ｔで積分をすると、

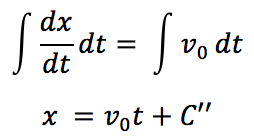
※C’’は積分定数

　となります。時刻0のときの位置を初期位置x₀とすると、

　積分定数C’’=x₀となり、このことから、

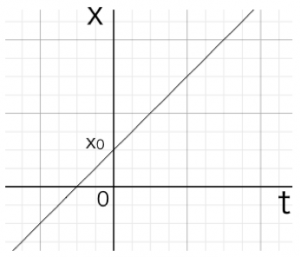
　となります。これをグラフにすると次ような１次関数になります。傾きが速度v₀を示しますね。

まとめ

今回は 「力と運動」 について、微積を使って考えてみました。高校の物理では微積を使わなくても学べますが、実は使ったほうがスッキリ理解できることもあります。次回は重力が働く場合の物体の動きについて考えていきます。

次の記事はこちら

物体はどう落ちる？ 微積でスパッと理解する落下の法則！（物理と微積 第２回）

科学のタネを発信中！

@kuwakoさんをフォロー

NEW　分解問題集　理科

• ７月２１日発売！『高校入試 分解問題集 理科』（学研）…難しい問題も小さな問題に分解することで、問題を解くことができます。そんな分解の技術が身につくように深く関わりを持って作りました。

７・８月のイチオシ実験！

夏でプシュッと爽やか実験！

小型で持ち帰れるよ！ペットボトルロケットを作ろう！

テレビ番組監修・イベント等のお知らせ

• ７月３０日（水）科学監修「TIF presents ONE SONG FES」（フジテレビ） 26:15~27:15
• 12月26日（土）　ナリカサイエンスアカデミー（教員向け実験講習会）開催

書籍のお知らせ

• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

各種SNS（更新情報をお届け！）

【日本語】X(Twitter)／instagram／Facebook　【英語】BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。