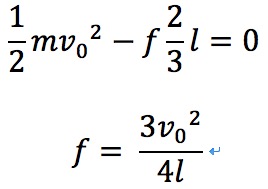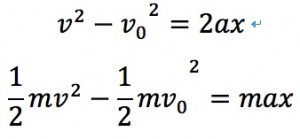「時間の無い式」と「エネルギー保存」の繋がりについて考えてみよう！
サイエンストレーナーの桑子研です。毎日が実験。
ちいさんから物理基礎に関して質問が届きました。ちいさんから了承を得たので、お答えしました（名前など一部改変しています）。
Q エネルギーの保存のつかいどころがわかりません！時間のない式ではだめなのでしょうか？
わたしは今年のセンターを物理基礎で受験する文系の者ですが、学校に物理基礎を受ける者がわたし1人しかおらず、物理の先生は理系の物理につきっきりでなかなか質問すら受け付けてもらえない状況でして…いつも(こちらから一方的に)お世話になっている桑子先生にお力を貸していただきたいのです。
早速質問で申し訳ございませんが、速さvを求める際に、”等加速度運動の公式を使うべきか、エネルギー保存の法則を使うべきか”を見極めるコツはありますか？例えば次のような問題の場合です。
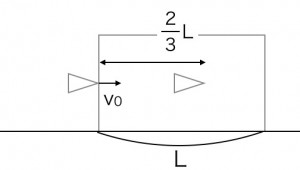
問題
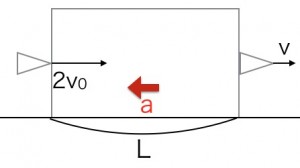
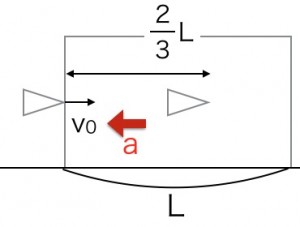
長さLの木材を図のように固定し、速さv0で弾丸を木材に向かって水平に打ち込んだところ、2/3Lの位置までめり込んで静止をしました。同じ弾丸を速さ2v0で打ち込んだところ、木材を突き抜けました。木材を突き抜けた後の速さを求めなさい。木材が弾丸に及ぼす力は弾丸の速さによらず一定とします。
解説を読んだところ、エネルギーの保存を使って解いてありました。
これを、等加速度運動の公式から時間tを除いた式(v^2-v0^2=2ax)で求めることはでき…ませんよね？初速v0、変位xが与えられており、加速度をma=Fから求めれば等加速度運動の公式で速さvが求められそうだな…と考えてしまい、上手く解を求めることができませんでした。
解答解説を読んで解を求めることはできたのですが、”どうしてエネルギー保存の法則を使うという発想に至ったのか？”がどうもよく分かりません…。
よろしくお願いいたします。
A 時間のない式で解けるはずですよ。
ちいさんありがとうございます。時間のない式で解けるはずですよ。というのも、この式はエネルギー保存の式と同じ意味をもっているからです。
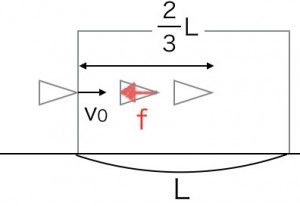
まずはエネルギーの保存でどのように解けるのかを考えてみましょう。次の図のように、はじめの弾丸の様子と終わりの弾丸の様子、そして抗力のした力をｆとしてエネルギーの保存の式を作ります。
式①
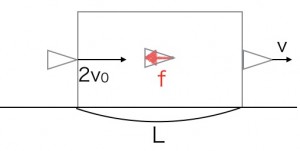
次に2v0で打ち込んだときの、エネルギーの保存の式を作ると、
このｆに式①のｆを代入して、ｖについて求めていくと、答えは
となります。
動画を使った解説も作りました！こちらを御覧ください。
次に時間の無い式で解く場合について紹介しましょう。弾丸は木材の中で一定の力を受けます。そのため一定の加速度で減速していきます。はじめの2/3lまでいったときの場合は加速度をa、とすると、
となります。同様に、貫通したときの場合は、
となります。２つの式を連立して加速度aを消すことによって同じ答えを導き出すことができます。
実は時間の無い式とエネルギーの保存は同じ式です。例えば時間の無い式の両辺に1/2mをかけてみます。
時間のない式
ここで右辺に運動方程式ma = Fを代入します。
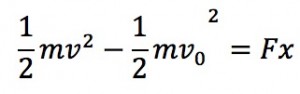
となり、整理すると、
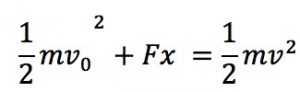
はじめの力学的エネルギー＋仕事＝おわりの力学的エネルギー
という式になりますので、同じ式になるというわけです。動画を使った説明はこちらをご覧ください。
エネルギー保存はいつ使えばいいの？
物理基礎でも問題に対して、どうやって使い分けるのか？がポイントになります。
方法としては、拙著ぶつりの１２３で紹介したのですが、問題をみたらまずはじめにエネルギーの保存が使えるかどうかを確認してください。だめそうなら、運動方程式という感じでいきます。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
５月のイチオシ実験！
キーンと冷えるドライアイス！気温が上がってくるこの時期・ドライアイスを使った昇華・凝結・等速度直線運動の実験はいかが？
液体ゼロ！ドライアイスが消えるまでの３時間を科学する（昇華・凝結・等速度直線運動）
テレビ番組監修・イベント等のお知らせ
- 4月30日（木）「THE突破ファイル」（日本テレビ）の科学監修を担当しました。
- 5月8日（金）理科教育ニュースを担当しました。
- 6月14日（日） 千葉大学インスタレーション「探究」にて講師を務めます
- 6月26日（金） 千葉大学の公開研究会（中学理科について授業公開予定）
- 7月18日（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
書籍のお知らせ
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
各種SNS（更新情報をお届け！）
X(Twitter)／instagram／Facebook（日本語）
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
