回折は波の子供（素元波）で考えてみよう【スマホで物理#08】
サイエンストレーナーの桑子研です。毎日が実験。
今日は素元波をつかって波の回折という回り込み現象を考えてみたいと思います。
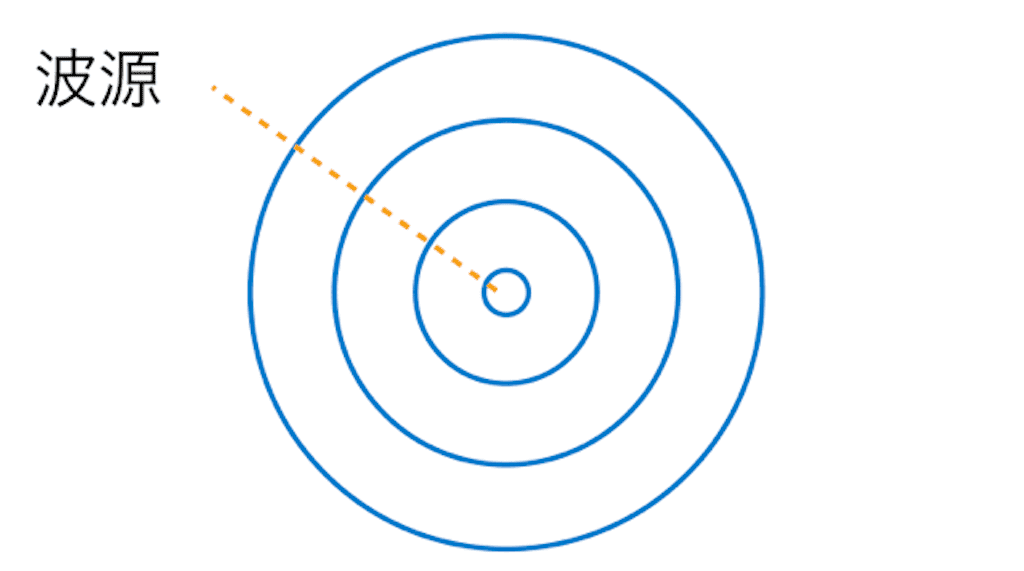
| ・波源を中心に円形に広がる
・進行方向と波面は垂直になる
|
#素元波 を使った直線状の波の考え方
お風呂の中で、水滴を落としてみると円形のきれいな波紋が広がっていきます。それぞれの波面（波形）は波源を中心にしたきれいな円となっています。これが#07でお話した素元波という「波の子供」の様子です。次の棒のような長いもので水面を叩いてみると、円ではなく叩いた棒と平行に、直線状の波面の波がおこって伝わっていきます。
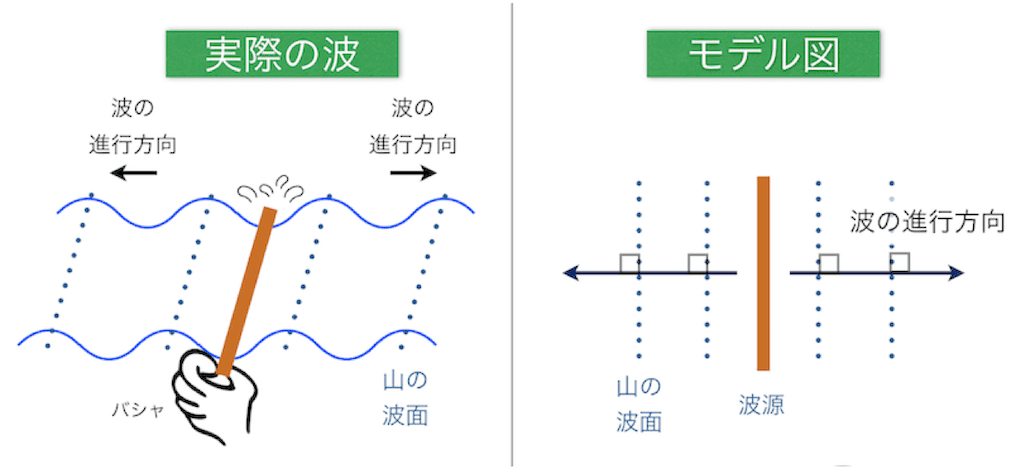
なぜこのような直線状の波面ができあがるのでしょうか。ホイヘンスの原理（ホイヘンス＝フレネルの原理）によれば、あるときの波面は、その前の波面から出た #素元波 の重ね合わせで表されます。
？？
どういうことでしょうか。どうみても円には見えないこの直線状の波面が、素元波の重ね合わせで表される？
次の図を見てください。
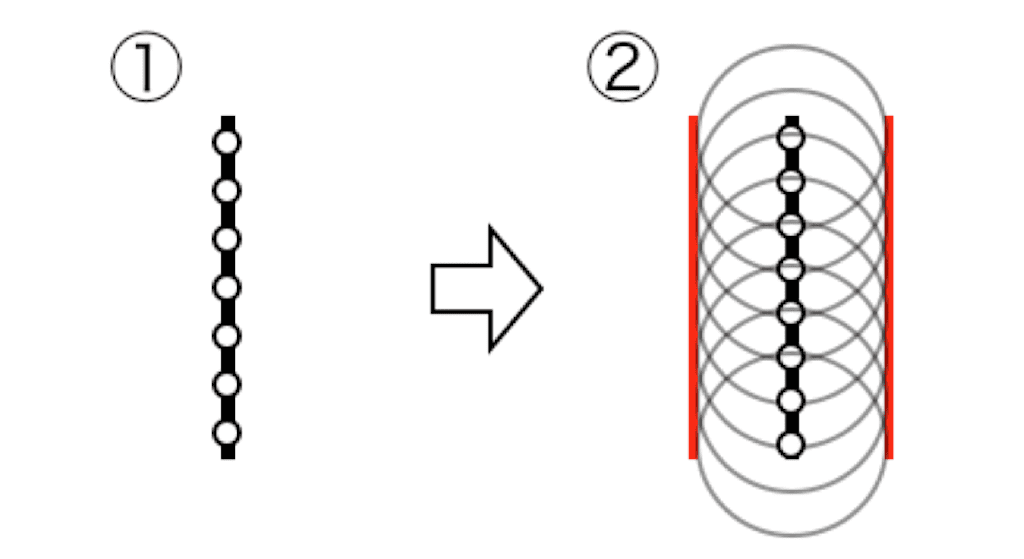
棒で水面を叩くと(①)、その棒の上にたくさんの素元波の波源が発生したと考えます。そして複数の波源からたくさんの素元波が発生します (②)。それらの波面が重なりあった場所に新たな波面(赤で示しました)が出来上がります。
動画でも撮影しました。こちらも合わせてご覧ください。
また実際にこの教材は触れるようになっています。こちらからお試しください。
このように考えると、たしかに素元波の集まりで直線状の波面を考えることができましたね。数学でも「直線は点の連なりである」と教えてもらったことがありますよね。なるほど。素元波はたしかに波の子供なのかもしれません。
またこの波面のできた場所を新たな波源として素元波を考えると（③）、次の時間での波面も直線状になるという考え方です。
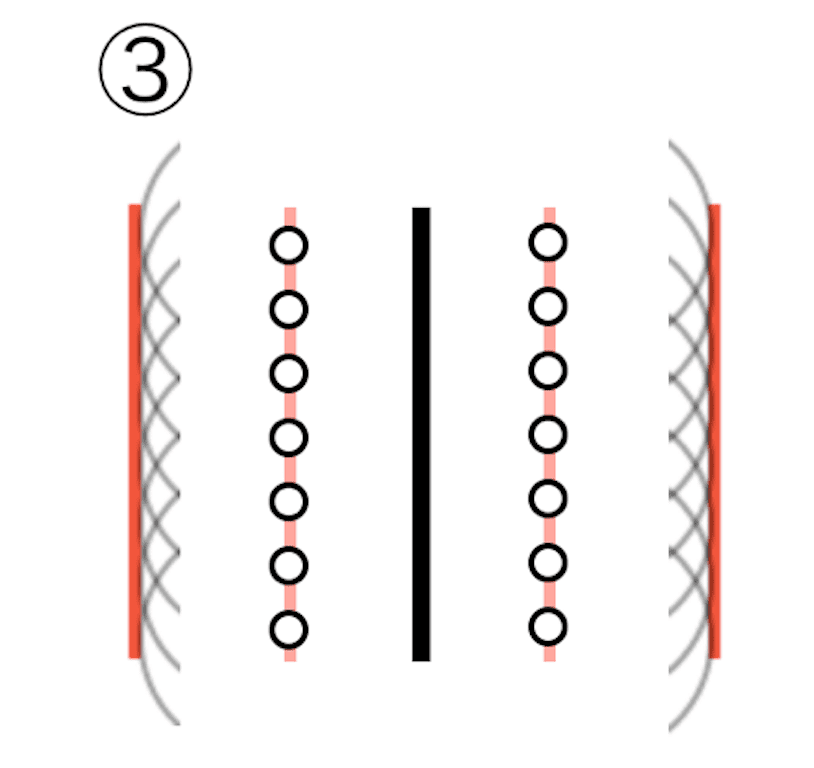
これは自然現象の様子とあっていますよね。
素元波を使った波の回折の考え方
次の図のように、堤防に小さな隙間が空いているところを想像してください。その隙間に波が入ってくると、波は隙間を通って一直線にすすむわけではなく(図左)、その隙間を中心として円形に広がって行きます(図右)。
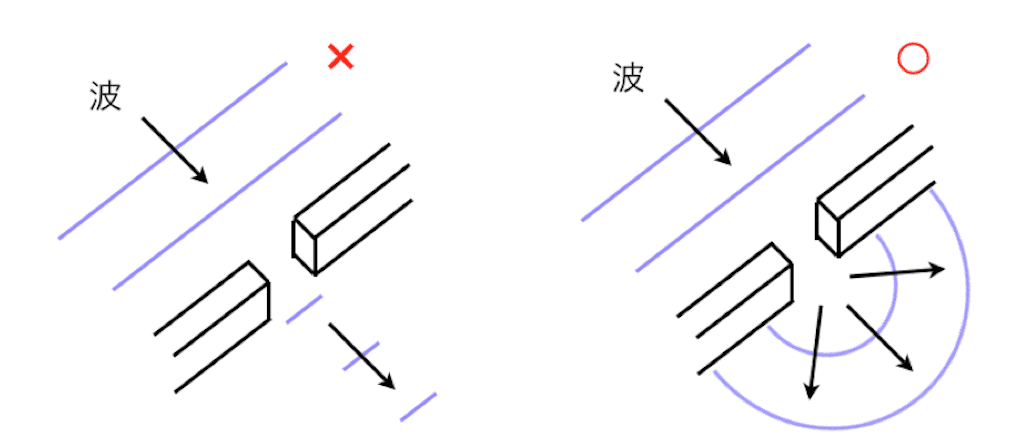
このような様子をよく見たことがありますよね。波がこのように回り込んで進んでいく現象を波の #回折 といいます。でもよく考えれば、これはとても変な性質に思えます。例えばボールを壁の隙間にむかって投げたとき、隙間を通り抜けた瞬間、ボールが分裂して飛んでいくというようなことはありません。
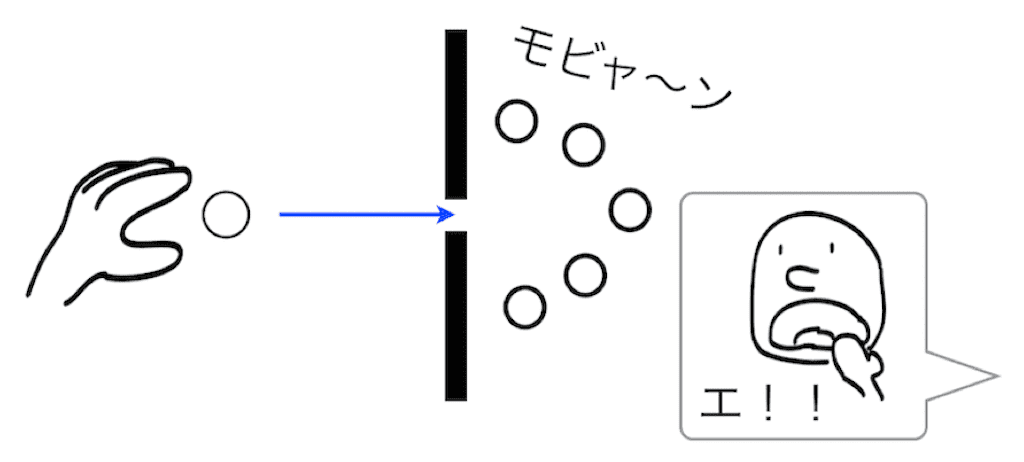
これを素元波で考えてみましょう。こちらの動画をまずは御覧ください。
この教材は触って学べるように作りました。こちらからお試しください。
次の図①のように、直線状態の波面がやってきました。直線状態波面は連続した点波源と考えることができます。
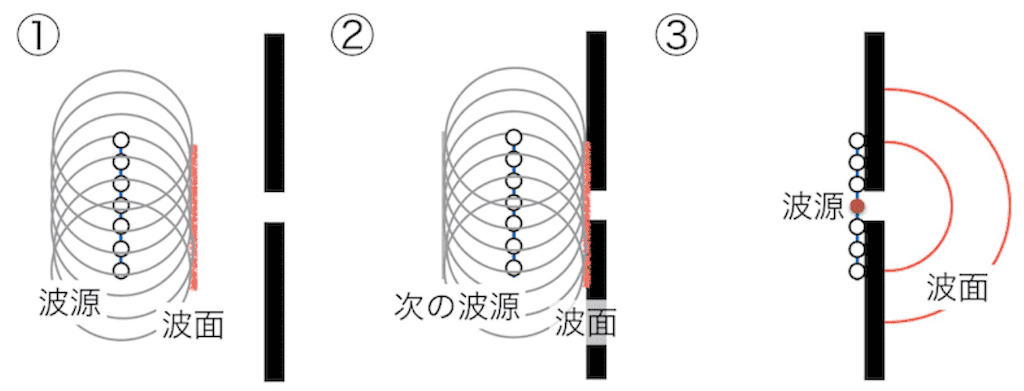
②のように壁に到達すると、③のように壁の上に点波源ができますが、隙間があいている赤い波源だけは、次の素元波を前方に出すことができ、隙間を通して円形の波面が現れます（壁にぶつかった波源は？というと消滅してしまうわけではなく、左方向に戻っていきます（反射））。
これが素元波を使った波の回折という現象の考え方です。このように素元波を使うと、回折の他にも波が曲がる理由（屈折）や波が戻ってくる理由（反射）などについても考えることができるのですね。
次回は波の性質その②「波の重ね合わせの原理」について見ていきましょう。
参考情報 動画授業
動画にて解説をしました。プリントをダウンドードしてご覧ください。
|
波のいろいろな性質について、ホイヘンスの原理をつかって統一的に説明をしてみましょう。 |
|
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
２月のイチオシ実験！梱包材で遊ぼう！
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう！→ やめられなくなる！静電気実験２０
体中に梱包材をはりつけてみよう！
テレビ番組等・科学監修等のお知らせ
- 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
- サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
講師等・ショー・その他お知らせ
- 2/20（金）「生徒の進学希望実現支援事業」研究授業＠福井県立若狭高等学校 講師
- 3/20（金） 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③ 11:20-12:20
- 7/18（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10（土） サイエンスショー予定
- 各種SNS X(Twitter)／instagram／Facebook／BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
