波のプロフィールを大公開！５つのキーワードと最強公式 v=fλ をマスターしよう【スマホで物理 #03-1】
サイエンストレーナーの桑子研です。毎日が実験！
音楽を聴くときの「音」、スマホで情報をやりとりする「電波」、電子レンジで食品を温める「マイクロ波」。私たちの生活は、目には見えないたくさんの「波」であふれています。これらの波は、一体何がどう違うのでしょうか？
その謎を解くカギは、波の性質を表すいくつかの「キーワード（物理量）」に隠されています。今回は、この波を解読するための特別なコトバと、それらが織りなす最も重要な「波の公式」について学んでいきましょう。この記事を読み終える頃には、波の世界がぐっと身近に感じられるはずです！
波の世界を旅する準備（前回の復習）
まずはおさらいです。波を理解するには、２種類のグラフが登場しましたね。
| ・y-xグラフ：ある一瞬を切り取った波の「写真」。空間的な形がわかる。
・y-tグラフ：ある一点の揺れを追いかけた「定点観測カメラの記録」。時間的な変化がわかる。 |
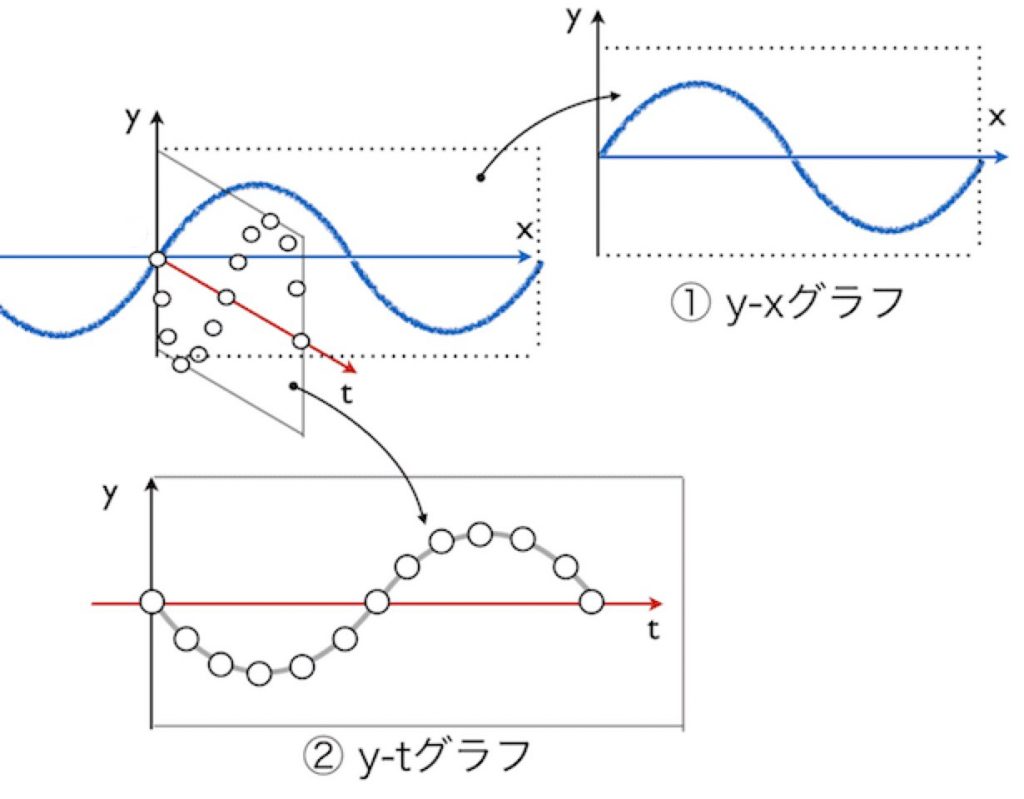
物理の世界では、距離を x や L [m]、時間を t [s] という文字で表すのがお約束です。これから、波のプロフィールを明らかにする５つの重要な物理量（キーワード）を、この２つのグラフから読み解いていきます。
波の「かたち」を捉える！ y-xグラフからわかるキーワード
まずは波の「写真」であるy-xグラフから見ていきましょう。ここからは波の「姿かたち」に関する情報がわかります。
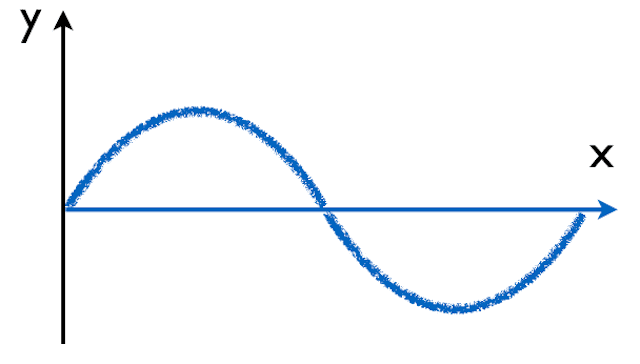
- 波長（はちょう）： λ （ラムダ） [m]波の山と谷のワンセット、つまり「一波ぶんの長さ」のことです。波の「歩幅」のようなものだとイメージしてください。記号の λ はギリシャ文字で「ラムダ」と読みます。なんだか強そうでカッコいいですよね！
- 振幅（しんぷく）： A （エー） [m]波の揺れの大きさ、つまり「中心からの最大の高さ」を表します。これは波が持つエネルギーの大きさと関係があり、例えば、音の波なら振幅が大きいほど「大きな音」に、光の波なら「明るい光」になります。山の頂上から谷底までの長さではないので、注意してくださいね。
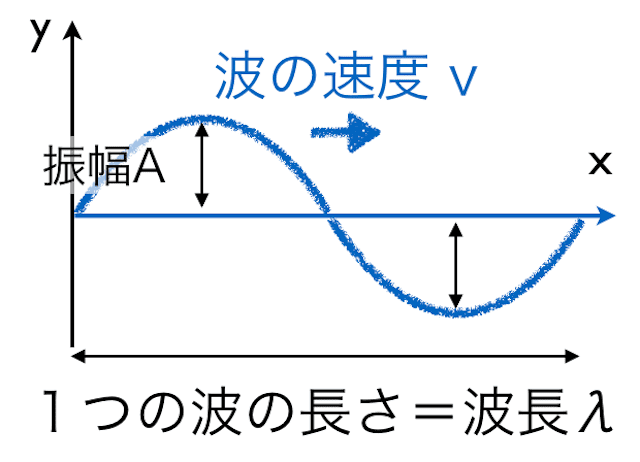
そして、この波そのものが進んでいく速さを速度 v [m/s]で表します。これはy-xグラフ一枚の写真だけではわかりませんが、波の進行方向を示す矢印と一緒に書かれていることが多いです。
波の「リズム」を感じる！ y-tグラフからわかるキーワード
次に、ある一点をじっと見つめた「定点観測」のy-tグラフです。ここからは波の「リズミカルな動き」に関する情報がわかります。
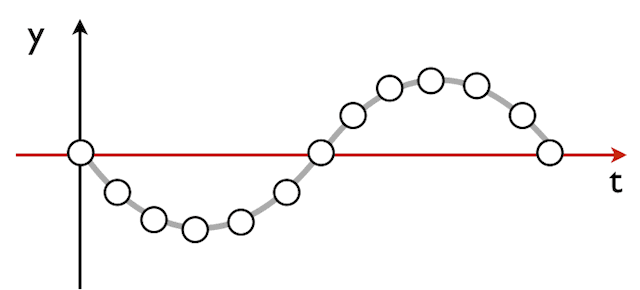
- 周期（しゅうき）： T （ティー） [s]観測している点（媒質）が、山→谷→山と「１回振動するのにかかる時間」のことです。これは、ちょうどその場所を１つの波が通過するのにかかる時間と同じです。波のゆったりとした「一回の呼吸」にかかる時間と考えると分かりやすいかもしれません。
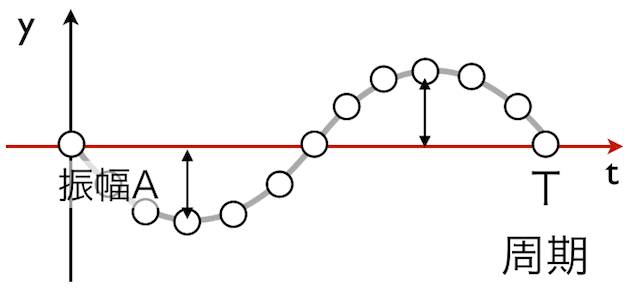
この「ある媒質が１回振動する ＝ １つの波がそこを通り過ぎる」というイメージは非常に大切です。こちらの動画で確認してみてください。
y-xグラフの λ と、y-tグラフの T は、見た目が似ているので混同しがちです。横軸が距離[m]なのか、時間[s]なのかを必ず確認するクセをつけましょう！
- 振動数（しんどうすう）： f （エフ） [Hz]周期とは逆に、「１秒間に何回振動するか」という波のせっかちさを表す量です。単位はHz（ヘルツ）。ラジオの周波数などで聞いたことがありますね。例えば、１秒間に２回振動すれば、振動数は f=2 [Hz] です。音の波では、この振動数が「音の高さ」を決めます。振動数が大きい（ヘルツが高い）ほど、高い音になるんですよ。
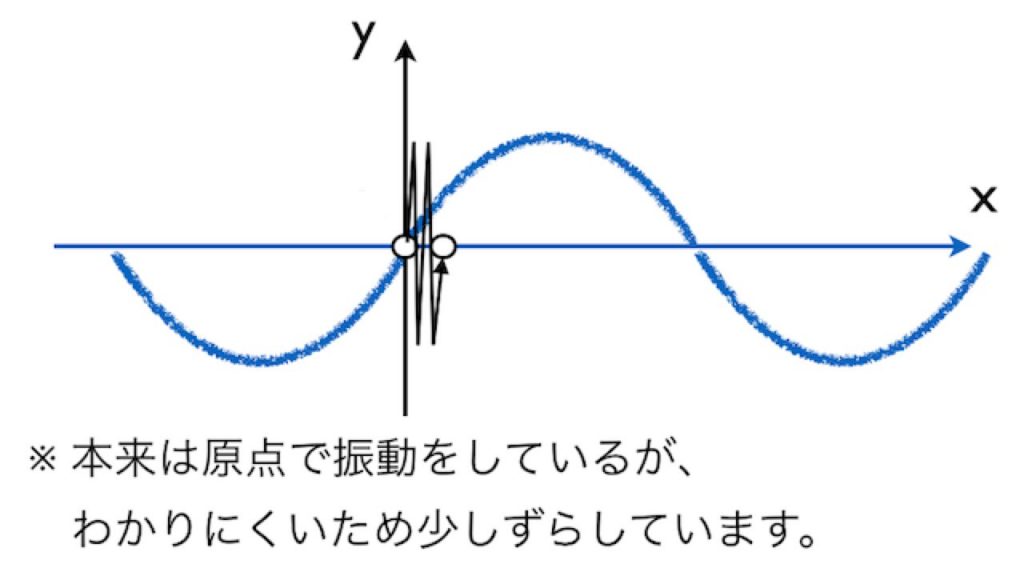
リズムと時間は裏返し？ 周期 T と振動数 f の秘密の関係
「１回振動するのにかかる時間（周期 T）」と「１秒間に振動する回数（振動数 f）」。この２つは、実は同じ現象を別の角度から見ているだけで、密接な関係があります。
考えてみてください。もし振動数が 2 Hzなら、１秒間に２回振動するわけですから、１回の振動にかかる時間は 1÷2=0.5 秒ですよね。つまり周期は 0.5 秒です。もし 3 Hzなら、周期は 1/3 秒、4 Hzなら 1/4 秒です。
表にまとめると、この通り。
| 振動数 f [Hz] | 1 | 2 | 3 | 4 |
| 周期 T [秒] | 1 | 1/2 | 1/3 | 1/4 |
そう、この２つは単純な逆数の関係になっているのです！
T=1/f
この関係式はとても重要なので、しっかり覚えておきましょう。
波の世界の最強方程式！ v=fλ
さて、いよいよクライマックスです。これまで学んだキーワードたちをつなぐ、波動分野で最も大切で美しい公式を紹介します。
原点から振動数 2 Hzで波が発生している状況を想像してください。
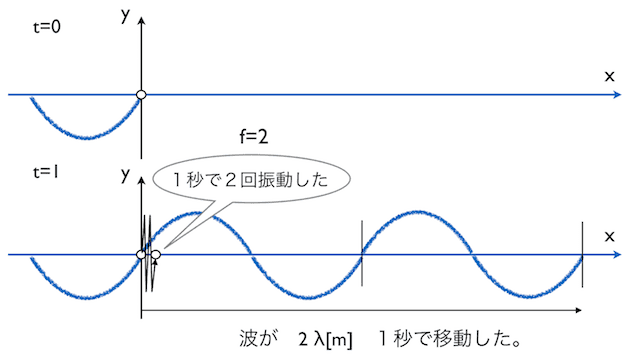
振動数が 2 Hzということは、１秒間に２回の振動が起き、結果として２個の波が送り出されることを意味します。１つの波の長さは波長 λ [m] でしたから、波の先頭は１秒間で 2×λ [m] 進むことになります。
「１秒間に進む距離」…これは、まさに「速さ」そのものですね！
このときの「２」という数字は振動数 f のことですから、以下の式が成り立ちます。
v=fλ
（速さ ＝ 振動数 × 波長）
波の「速さ」、波の「リズム（振動数）」、波の「かたち（波長）」という、波の重要な３つの要素が、この１つのシンプルな式で見事に結びついているのです。これが波の世界の最強方程式です！
以上が、波の世界を旅するための基本的なキーワードと公式です。最後に一覧で確認しておきましょう。
これらの言葉の意味をしっかり理解すれば、波の現象はもう怖くありません。次回は、これらの知識を使って、さらに波の奥深い世界を探検していきます。
続きます。
波については拙著も参考にしてみてください。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
科学のネタチャンネルでは実験動画を配信中！
４月のイチオシ実験！
- 光の魔法CMYウォーターキューブ：光の魔法を体験せよ！水を注ぐと新たな立方体が出現する魔法のような実験です。
テレビ番組・科学監修等のお知らせ
- 4月9日（木）「THE突破ファイル」（日本テレビ ）の科学監修を行いました。夜7時〜となります。
書籍のお知らせ
- サクセス15 ４月号にて、野球の科学について記事を執筆しました（2026/3）
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
講師・ショー・研究等のお知らせ
- 3/20（金） 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表しました。
- 6/14（日） 千葉大学インスタレーション「探究」にて講師を務めます
- 7/18（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10（土） 秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
- 各種SNS X(Twitter)／instagram／Facebook／BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
- 【科学監修】コイン2枚で袋が開く！科学監修者が教える「テコの原理」活用術（「教科書で習ったアレ」テレビ朝日）
- イチョウは広葉樹じゃない！？扇形の葉っぱに隠された「生きている化石」の正体（植物図鑑）
- そのタンポポ、「一つの花」じゃないんです！顕微鏡でのぞく驚愕の集合体「頭状花序」の秘密
- 瞬間の奇跡！水風船の中に隠れた「慣性の法則」を捕まえろ！
- 遊びが学びに変わる瞬間！スピログラフの幾何学模様に隠された「数学の魔法」（Desmosプログラミング）
- 数万の価値が無料に！？数式グラフ化の神アプリ「Desmos」で視る電気の丘
- 鼻歌まじりの決死圏？月面ジャンプに隠された「真空と重力」の驚きのストーリー（アポロ計画）
- 見えない電位を立体で捉える！ランチボックスの蓋で作る驚きの科学工作
- 影が教える物理の秘密！等速円運動と単振動の意外な関係（単振動と等速円運動のつながり）
