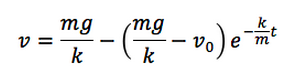雨粒の落下と加速度のa-tグラフを微積で考える!(高校物理と微積分)
サイエンストレーナーの桑子研です。毎日が実験。

前回、「雨の速度はなぜ一定になるのか?」について、微積分を使った解説をお届けしました。すると、さっそく次のような質問が寄せられました。
Q「雨粒が初速度0で落下するとして、雨の落下のv−tグラフはわかりましたが、加速度の様子(a−tグラフ)はどうなるのでしょうか?」
今回はこの質問にお応えしていきたいと思います。微積分を少し取り入れるだけで、イメージだけでなく「数式的にも納得できる」面白さが味わえます。授業で生徒に問いかける題材にもピッタリなので、ぜひ準備の参考にしてください!
まずはイメージから
前回整理したように、空気抵抗のある雨粒の運動は、次のような式とグラフで表されます。
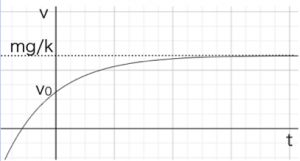
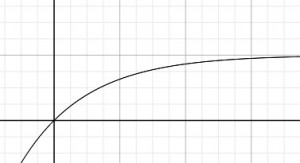
もし初速度 v_0 が0場合、つまり「静かに落下し始めた雨粒」の運動は、さらに次のような数式とグラフで表されます。
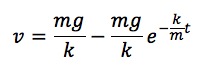
このグラフの様子から、加速度(a-tグラフ)はどうなりそうでしょうか?
• 雨粒は落下し始めると、最初は急激に速度が変化します。
• しかし、空気抵抗がだんだんと大きくなって、速度の変化は徐々に緩やかに。
• 最終的には、速度の変化がほぼなくなり、一定になります。
つまり、加速度は最初は大きく、その後なだらかに減少し、最終的に0に近づくそんなイメージのグラフが予想されますね!
数式で確かめよう
加速度は、速度の時間微分です。では、実際に速度を微分してみましょう。
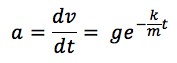
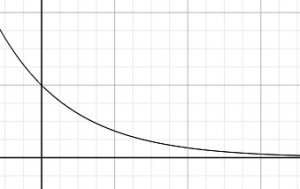
計算してみると、時刻0のとき、加速度は重力加速度 g になります。これは、落下開始直後には空気抵抗がまだ働いていないので、「ただ重力だけ」で加速していることを意味しています。その後、時間が経つにつれて、空気抵抗が増していくため、加速度は徐々に小さくなっていきます。そして、最終的に加速度は0になり、速度が一定(終端速度)に達するわけですね。グラフにするとこんな感じです。
これが、加速度の a−tグラフです!
ちょっとしたことですが、微積分を使うとイメージと数学がぴったり一致して、より深い理解につながります。授業でも「なんとなくこうなる」という感覚から、「数式でも確かめられる!」という驚きを与えることができます。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20

テレビ番組等・科学監修等のお知らせ
- 2/9日(月)まで配信中 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師等・ショー・その他お知らせ
- 2/20(金)「生徒の進学希望実現支援事業」研究授業@福井県立若狭高等学校 講師
- 3/20(金) 一般社団法人 日本理科教育学会 オンライン全国大会2026にて、「慣性の法則の概念形成を目指した探究的な学びの実践」について発表予定です。
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定