目に見えない電場と電位を”見える化”！Macの隠れた名ソフト「Grapher」で物理が超面白い！

サイエンストレーナーの桑子研です。毎日が実験。

あなたは電場と電位をイメージできますか？Macに標準で搭載されているGrapherというソフトを使うと、なんとそんな悩みが一気に解決してしまうんです。

「電場と電位」という単元は、高校物理の初学者にとって鬼門ですよね。言葉の響きが似ている上に、どちらも目に見えない概念。授業でどれだけ丁寧に説明しても、生徒たちの頭の中にはモヤモヤとした霧が立ち込めてしまいがちです。

「『位』は位置エネルギーのようなもの、『場』は力だよ」と説明したところで、なかなかピンとこないのが正直なところでしょう。概念をただ言葉で説明するだけでは、生徒の“腑に落ちる”感覚には繋がりません。そこで今回は、見えない世界を可視化する魔法のツール「Grapher」を使った、視覚で納得できる授業実践法をご紹介します。これはMacに標準搭載されているソフトなので、特別に準備するものは何もありません。いつもの授業にたった一つ加えるだけで、生徒たちの「わかった！」という歓声を引き出すことができるはずです。

授業準備：Grapherで電場と電位のビジュアル化に挑戦！

まずは、Grapherを使って電位のイメージを掴んでみましょう。電位は、ちょうど地理の「等高線」のようなものです。点電荷が作る電位を3次元グラフで表現すれば、その形状を立体的に捉えることができます。Grapherなら、数式を入力するだけで、瞬時に美しいグラフが描画されます。

【手順】

Grapherを起動する

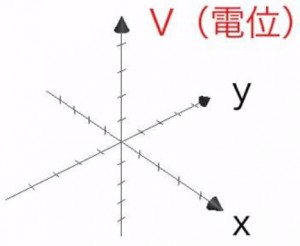
「Grapher」アプリを開き、「3次元グラフ」を選択します。縦軸がz軸となり、これが電位、つまり「高さ」を示します。

点電荷の電位を可視化する

点電荷が作る電位の数式は、V = kQ/r ですね。これを3次元に拡張して、Grapherに入力してみましょう。クーロン定数kと電気量Qは、今回は分かりやすさのため「1」とします。

【入力する数式】

z = 1/sqrt(x^2 + y^2)

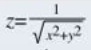
【ワンポイント】

物理では、このように大まかな形を理解したいときには、定数をすべて1にするとシンプルに考えられます。このような“ざっくり思考”も物理を学ぶ上でとても大切です。

グラフを観察する

Returnキーを押すと、グラフが生成されます。まるで山のような形ですね。これがプラスの電荷が作る電位の形です。生徒たちにグラフを様々な角度から観察させてみましょう。

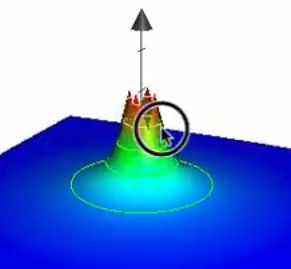
この山の傾きが「電場」に相当します。傾きが急な中心付近ほど、電場が大きいことが視覚的に理解できます。

等電位面を観察する

グラフを真上から見ると、同心円が描かれています。これが等電位面です。

中心に近いほど等電位面が密になっていることから、電位の傾き（＝電場）が急であることがわかります。

負の電荷も描いてみる

次に、負の電荷も追加してみましょう。

【入力する数式】

z = -1/sqrt(x^2 + y^2)

マイナス記号を付けるだけなので簡単ですね。すると、山とは逆に、下向きに伸びる「穴」ができます。これが負の電荷が作る電位の形です。

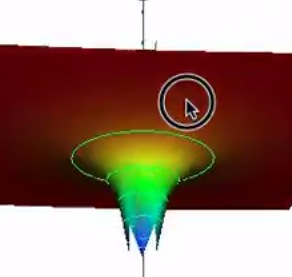
複数の電荷を重ね合わせる

いよいよ本番です。冒頭の問題のように、x-y平面に2つのプラスの等量の電荷を置いてみましょう。

【入力する数式】

z = 1/sqrt((x-1)^2 + y^2) + 1/sqrt((x+1)^2 + y^2)

この数式によって、2つの電荷がx軸上でそれぞれx=1とx=-1の位置にずれます。

グラフを観察し、電場を考察する
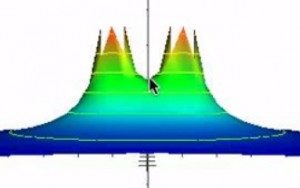
グラフを描画すると、双子の山「二子山古墳」のような形が浮かび上がります。

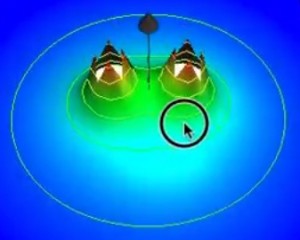
このグラフを横から見てみましょう。

グラフの中心、原点の部分に注目してください。山の傾きはどうなっていますか？そう、平らになっていますよね。つまり、傾きがゼロ。
これは、電場がゼロであることを意味します。

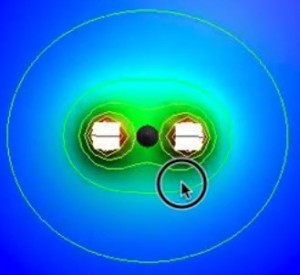
等電位面を確認する

グラフを真上から見ると、原点の部分を等高線がほとんど横切っていないことがわかります。傾きがないため、等高線も集まってこないのです。

これで、頭の中で考えていた答えが、目で見て納得できる答えに変わりましたね。

さらなる応用：波の可視化にも挑戦！

Grapherの面白さは、電場や電位だけにとどまりません。皆さんが頭の中で苦労して描いている「波の式」も、3次元で可視化することができるんです。

【入力する数式】
y = A * sin(2 * PI * (x/lambda – t/T))
(※A=振幅、PI=円周率、lambda=波長、t=時間、T=周期)

この式をGrapherに入力してみてください。目の前で波がうねりながら進む様子を、立体的に体験できるはずです。生徒たちと一緒に「どんな図ができるかな！？」とワクワクしながら試してみるのも、良い授業のスパイスになるでしょう。

まとめ

いかがでしたか？言葉だけでは伝わりにくい物理の概念も、このように立体的に可視化することで、生徒たちの理解を劇的に深めることができます。Grapherは、Macに標準搭載されているため、特別な準備は不要。WindowsやiPadでも同様の機能を持つソフトはありますので、ぜひお手持ちの端末で試してみてください。

 

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！