浮力の公式の求め方・導出方法（アルキメデスの原理）

サイエンストレーナーの桑子研です。このサイトで科学を一緒に楽しみましょう。

『きめる！センター試験物理基礎』の特設サイトに戻る

 

図は同書籍より引用

水の中に物を入れると、上向きの力がはたらいて、軽くなったように感じます。これは浮力という力が、上向きにはたらくためです。浮力の公式は次のようなものがあるのですが、参考書『きめる！センター試験物理基礎』の中では導出をすることが誌面の関係からできませんでした。

浮力F　＝　ρ_WV_Wg

　ここで液体の密度をρ_W[kg/m³]、物体の水に沈んでいる部分の体積をV_W[m³]としています。ここではこの公式がどのように出てきたのかについて導出方法を説明したいと思います。

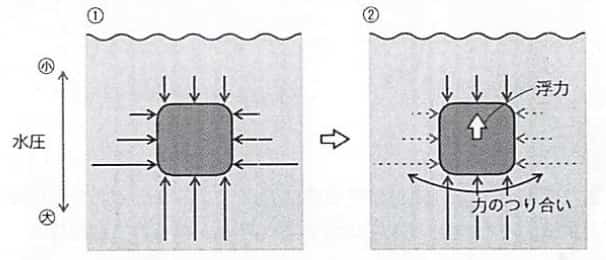
導出の中で大切なのは、浮力は水圧による力の合力であるということです。次の図①のように、水圧はさまざまな方向から物体を押しますが、深さによって変化します。その大きさは深さに比例します。

図は同書籍より引用

　これらを合成すると、②のように左右方向はキャンセルされ、下の力と上の力の差として上向の力が現れます。これが浮力です。

では実際に求めてみましょう。図のように密度ρ[kg/m³]、面積S [m²]、長さL [m]の円柱を、密度ρ_W[kg/m³]が水の中に沈んでいるとします。液面から円柱の上面までの深さをh[m]、重力加速度の大きさをg [m/s²]、大気圧の大きさをP₀[Pa]とします。

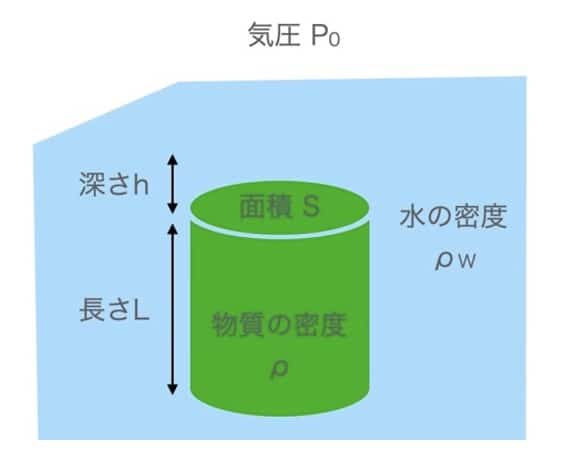
まずは上面の水圧P_Uを求めましょう（UはUPで上面という意味を持たせました）。深さh[m]での水圧は、「水圧の式」から

となります。水圧の公式を忘れてしまった人はこちらをご覧ください。

P＝ρhgって何？高校生のための水圧の公式まるわかり講座（きめる！センター試験物理基礎）

同様に、下の面の水圧P_Dを求めます（DはDownで下面という意味を持たせました）。深さh+L[m]での水圧は、

これらを上の面を押す力に直していきましょう。F=PSより、上面を押す力は、

同様に下面を押す力F_Dは、

浮力は上・下の圧力による力の差なので、②から①を引いてみましょう。

物体の体積Vは、SLなので、

浮力F　＝　ρ_WV_Wg

　となり、導出することができました。今回は簡単のため円柱を使って求めましたが、どんな形の物体に対しても言えるのがアルキメデスの原理のすごいところです。

なお、ここで実際にある物体が浮くのか沈むのかについても、考えてみましょう。鉄の塊である船がなぜ浮くのか？ときになる人もいますよね。

ある物体にはたらく重力はW=ｍｇです。また物体の密度ρを使うと、ｍ＝ρVより、

物体が浮くためには、重力よりも浮力のほうが大きくなればいいから、

浮く条件

よって、ρ<ρ_Wのとき物体は浮くことになります。密度の違いなのですね。

船は鉄を薄く伸ばして、全体の体積を大きくすることで、水よりも船全体の密度が小さくなって浮くことになります。

『きめる！共通テスト物理基礎 改訂版』著者特設の学習補助サイト（動画やシミュレーションを用意しました）

 

科学のタネを発信中！

@kuwakoさんをフォロー

５月のイチオシ実験！

キーンと冷えるドライアイス！気温が上がってくるこの時期・ドライアイスを使った昇華・凝結・等速度直線運動の実験はいかが？

液体ゼロ！ドライアイスが消えるまでの３時間を科学する（昇華・凝結・等速度直線運動）

テレビ番組監修・イベント等のお知らせ

• 4月30日（木）「THE突破ファイル」（日本テレビ）の科学監修を担当しました。
• 5月8日（金）理科教育ニュースを担当しました。
• 6月14日（日）　千葉大学インスタレーション「探究」にて講師を務めます
• 6月26日（金）　千葉大学の公開研究会（中学理科について授業公開予定）
• 7月18日（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。

書籍のお知らせ

• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
  
  
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
  

各種SNS（更新情報をお届け！）

X(Twitter)／instagram／Facebook（日本語）

BlueSky／Threads（英語）

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。