運動方程式をマスター!束縛力について詳しく知ろう
サイエンストレーナーの桑子研です。このサイトで科学を一緒に楽しみましょう。
高校生のみなさんは夏休みの勉強はすすんでいますか?
面の形や糸の長さを保とうとして、面や糸が及ぼす抗力や張力のことを「束縛力(拘束力)」といいます。運動方程式を使いこなすためには、この束縛力の理解がとても大切です。今回の校内で実施を考えている夏季講座では「束縛力」について、マスターしてもらうための内容をメインにすえてテキストを作っています。
束縛力の難しくて面白いところは、計算する前にはどのような大きさなのかが与えられたものではないというところです。重力やばねの力などは、計算する前から決まっているのですが、糸の力や張力はその状況(束縛条件)に合わせて計算することによって、力の大きさが決まります。
これらの束縛力の大きさは、糸が伸びないということや、曲線の形などという糸や面の条件、「束縛条件(拘束条件)」によって決まります。
例えばこんな問題の場合については、A、Bそれぞれの運動方程式を作ることができます。

m1>m2の場合は、
m1a = m1g − T(下向きを正とした)
m2a = T − m2g(上向きを正とした)
このときの条件として、糸が軽い糸であるということと、糸が伸び縮をしないということを条件として、2つの式でTを同じにしてあること、またaが同じになっていることを使っています。
このとき「aが同じ」ということは糸が伸び縮をしないという拘束条件を自然とつかっていて、本来であれば、
m1α = m1g − T(下向きを正とした)
m2β = T − m2g(上向きを正とした)
糸の拘束条件から
α=β
と書くほうが丁寧です(わかりきっているので書きませんが)。
ただし、次のように滑車さえも上に加速しているときは、拘束条件を丁寧に考えて、数式を一つ増やす必要がでてきます。
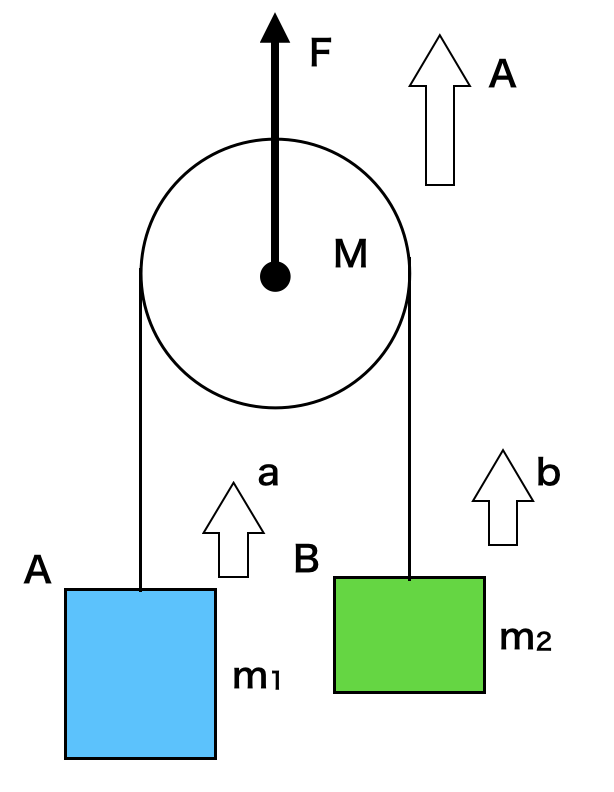
と、こんなお話をしながら、運動方程式をいろいろなシーンでたてる練習をしていこうかなと思っています。
[amazonjs asin=”479804301X” locale=”JP” title=”これだけ!高校物理 力学編 (これだけ!シリーズ)”]
科学のタネを発信中!
ニュースレターを月1回配信しています。
[subscribe2]
登録はこちらから
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20

テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日 科学監修をした番組が放送予定です。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。


