センター試験の解説に戻る

大学入試センター試験新テスト（大学入学共通テスト）物理の施工問題（プレテスト）を解いてみた。

入試改革の一つとなる、新テスト（大学入学共通テスト）の「平成29年度試行調査（プレテスト）の問題」が出てきましたが、皆さんはもう解いてみましたか？　対象となるのは教員と、現在中学３年生の生徒可と思いますが、ぼくは物理が専門なので、物理について実際に解いてみました。解説・感想も含めてまとめてみたいと思います。なお施工問題についてはこちら「平成29年度試行調査_問題」にアップロードされていますので御覧ください。

またこちらに書かれているように、

今回の試行調査で出題された問題の構成や内容は、必ずしもそのまま平成３２年度からの大学入学共通テストに受け継がれるものではなく、実際の大学入学共通テストの問題構成や内容等がどのようなものになるかは、今回の試行調査の解答状況等の分析を踏まえて検討されます。

あくまで調査的な側面が強いということも念頭に読み進めていただければと思います。大きな方向性としては、今回の調査のような問題を入れていきたいというメッセージだとは思います。

問題構成

第１問　小問集合　→　問６までの６問構成（多い！）

第２問　実験データから考察する問題　→　単振り子の周期の公式を延々と…

第３問　A・Bの構成で、車の運動（力学）と比熱（熱力学）に関する問題　→　グラフ用紙がついている！

第４問　電磁誘導に関する問題　→　２問しか問いが無い！

という感じで、波動については大問では扱われませんでした（原子については第３問で少し扱われています）。

全体の感想「これは１時間では解けない！」

こりゃ難しいぞ…。

全体を解いてみての感想ですが、時間がたりない！と思うはずです。物理という科目自体の特性を考えると、もともとが考える科目となっているために、解いてみるとわかるように国語や社会ほどの大きな変更があるわけではありません。問題１つ１つで「考える」ということに重きをおいているということは変化がないといえます。

ただし、データを分析する問題も出題されるなど、受験生がその場で臨機応変に物理知識がなくても考えれば答えが導けるような問題も出題されるようになっています。

ただしデータ分析をする上で、手間のかかる計算も多かったので、電卓を使ってぼくはときましたが、これを電卓を使用せずに１時間で解くとすれば絶対的な時間不足となる可能性がありあす。

また分野に関しても大きな偏りが出てきなす。今回であれば単振り子の周期の公式だけで大問が１つさかれているので、２５点くらいは差がつくのではないでしょうか。事前に学校等で実験をしているのかどうかが受験生にとってみれば大きな有利不利につながるといえます。これを今後のメッセージとらえると、学校でより多くの実験を行うということが必要になってくるでしょう。これは個人的には良いとこと思っています。

今の過程のセンター試験は「広く・薄く・全分野を」という傾向がありますが、今度のセンターは「狭く・濃く・データ分析も」ということがいえるとおもいます。今までのセンターの問題も残しつつも（第１問）、データ分析もある盛りだくさんの内容、受験生にとってみると物理知識は今まで同様に必要で深くきかれてしまうので勉強がしにくくなり、私大の個別入試や東大・東工大のような問題に近くなったことがいえます。

時間も含めて難易度が段違いに上がったので、今の対策のままで生徒が受けたとしたら、平均点が３０点台や４０点台になってしまうことが予想されます。

解答・解説とポイント

それぞれ大問ごとに見ていきましょう。

※　なお解説については間違いがある可能性がありますことご了承下さい。もしお気づきの点がございましたら、ご連絡いただければ検討をして訂正させていただきます。

第１問

問１では作問の「ねらい」については次のように述べられています。

物理的な事物・現象に関する原理・法則についての理解を基に，力学，電磁気，波動，原子物理等を題 材として，データや実験結果を適切に取り扱って解釈する力を問う。

ちょっとむずかしそうにかかれていますが、過去のセンター試験の問題をそのままつかった小問集合でした。全分野がまんべんなくでていますが、波動の問題が２つあり、６問の問題構成と従来のセンター試験よりも多めの小問数となっています。

実際解いてみると、「ねらい」で述べられている「データ」というのがあまり見当たらなかったので、今後は実験のデータが提示されるような問題もだそうとしてくるのかもしれません。第１問の解説はそのようなわけで割愛させていただきます。

第２問

解説

問１

単振り子の周期の公式では、

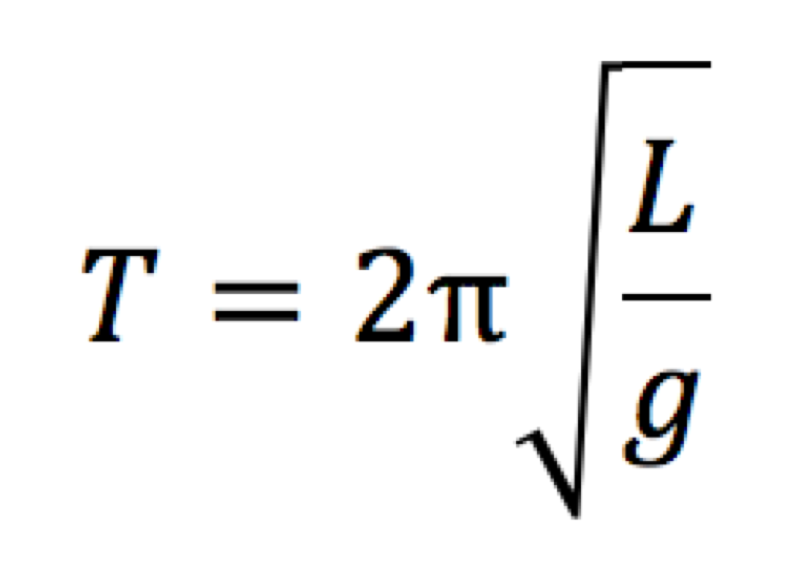
Lはヒモの長さを示しますが、ヒモの端から、おもりの重心までの距離ということがポイントになります。

ブランコの周期を短くするためには、ヒモの長さを長くする必要があります。そのため、選択肢の③のようにぶらんこのヒモを直接短くしたり、①のようにブランコの上に立つことによって、ブランコのヒモのはじまりから重心までの距離を短くするという方法をとれば良いことになります。

感想

面白いのが問題文の中で「該当するものがない場合は０を選べ」と、該当するものがないという可能性も含めてきたことです。このおかげで、問題の想定範囲がグッと広がり、受験生にとって難しくなったと思います。ただし施工問題では「０」となるものはどれもありませんでした。

問２

データを見て判断をすると、端で測定した場合のほうが１つ１つのデータのバラ付きが、中心で測定した場合とくらべて大きいのがわかります。そのため④を選びます。

ばらつきが明らかに左のほうのデータを見ると大きい

感想

表の平均値の値がほぼおなじになっているので、０と④で迷いました。指導書等で中心で測定するということが書いてあり、実際に中心で学校の実験でも同じようにやっていたのですが、恥ずかしながら端だとこういった誤差がでてくるのかと問題を解いていて勉強になりました。

問３

単振り子の周期の公式の条件としては、「振れ幅（角）が非常に小さいときに」という条件がつきますが、この問題ではそのことが問われています。データをみると、１０°、４５°、７０°と周期が角度によって変わってきているのがわかります。

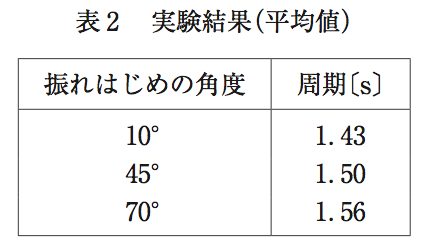
そのため、表１と表２を見ると１０°のところでは周期が同じくそろっていますが、４５°、７０°となると、選択肢②のようにデータからも実測値と計算値のさが大きくなっていくことがわかります。

また選択肢③のように表２から、角度が大きくなっていくと周期も大きくなっていくということが予想されます。

問４

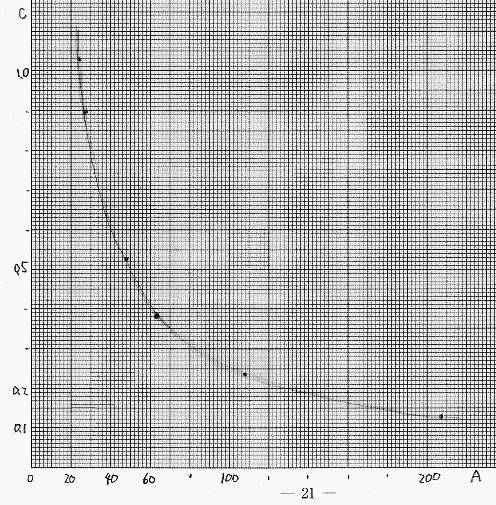
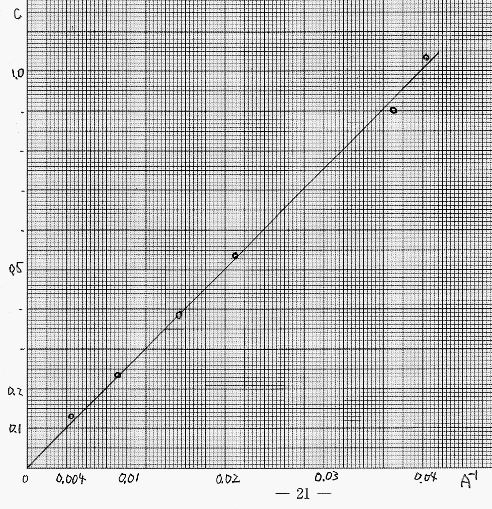
グラフを作るときに、どのようにして計算値と比較をするのかという問題です。今回は振り子の長さを変えたときに、周期がどう変わるかを調べた実験なので、縦軸には周期を、横軸には振り子の長さをとります。また振り子の周期の公式を、

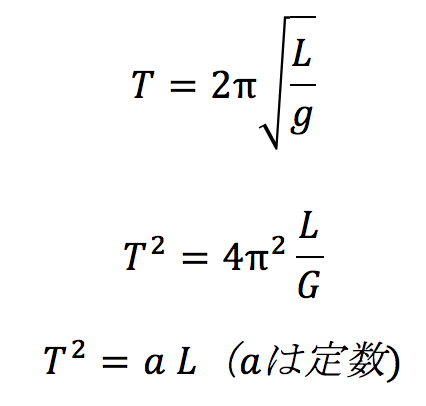
という形にもっていき、縦軸にT²と横軸にLの関係をプロットすることによって、１次関数になるのかどうかを確認することができます。答えは横軸が選択肢①、縦軸が⑥です。

問５

おもりに乗った立場で考えてみましょう。振り子運動ではおもりは円の中心方向に動くことはありませんから、つねにつりあった状態になっています。ですから、張力によって常に重力分を支える必要があります。

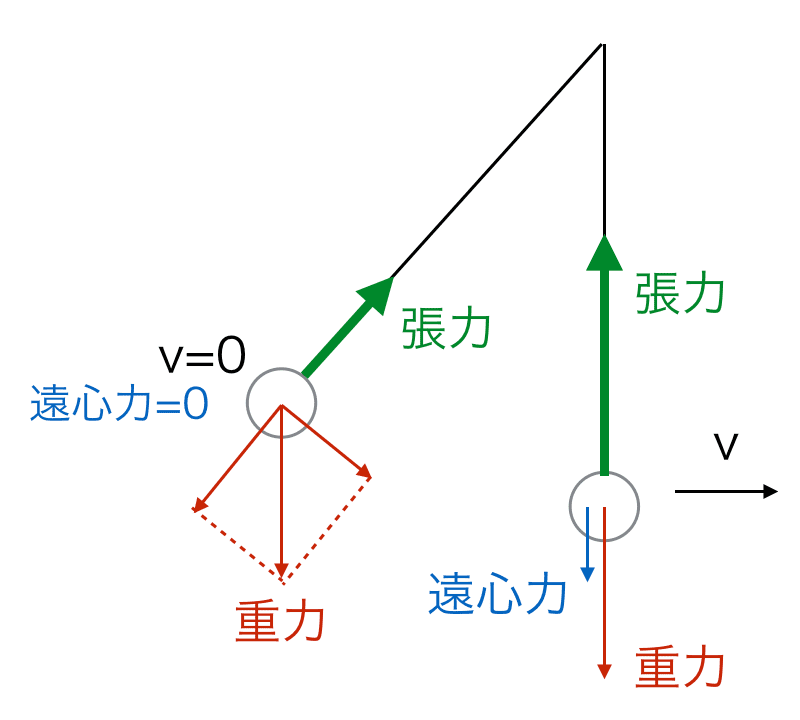
両サイドでは速度が０となっており、瞬間的に遠心力ははたらかないので重力の分解された成分を支えるだけでよいのですが、振動の中心である最下点では重力に加えて速度が出ているため遠心力の分も支える必要があるので、張力はおのずと最大となります。答えは④です。

第２問全体の感想

第２問の「ねらい」は次のように書かれています。

ひもやばねにつるされた物体に見られる周期運動についての理解を基に，小学校における学習で取り扱った振り子の実験を題材として，新たな情報を比較・分析したり統合したりすることで考察・判断するなど，課題を解決する力を問う。

まずは、ねらいのように実験の問題を扱うということに好感を覚えました。ただし実験を学校でやってきている生徒とやってきていない生徒では、狙いに「新たな情報」とありますが、この新たなということで大きな差がでてしまう問題でもあると感じています。

逆に良いほうに考えると、今まで高校で実験をたくさんやってきている学校のほうが有利となりますので、実験を重視した授業の展開が促進されるという可能性があります。入試が変わると授業が変わるという良い例になるかもしれません。

今回のように教科書にのっている、多くの学校で行うであろう実験を題材とした問題が今後出題されるとすると、出題の幅が限られるようにもおもいます。

周期の公式と振り子１本で、問１〜５までいろいろな角度から聞いてきているので、受験生にとっては当たりハズレが大きくなってしまうでしょう。いろいろな知識を問うということはできなくなるところはデメリットですね（メリットの裏返しでもあります）。

第３問

A

問１

ABを要する時間の最小値を求めるためには、ABをできるだけ速い速さで車が移動しなければいけません。そのための速さをまずは求めましょう。速さの条件には２つあり、まわるときの向心加速度の最大値（1.6m/s²以下）と、道路の制限速度(2.5m/s以下)の２つがあります。

まずは円運動の制限向心加速度の最大値1.6m/s²から、円運動をするための速さを計算をしてみます。このときの速さを加速度と速さの関係から求めると、

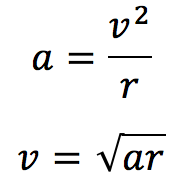
より、aに1.6m/s²を、rに400mを代入すると、v=25.2m/sとなります。もう一つの条件である道路の制限速度の25m/sをわずかに超えてしまいました。

もしこの速さが20m/s、25m/sよりも小さい値であれば、20m/sで計算をする必要がありますが、今回は25m/sよりも大きかったので、道路の制限速度である25m/sで走行をするのが最大であるということがわかります。このときAからBを走行するのにかかる時間ｔは、

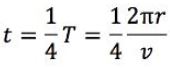
となり、vに25を、rに400を代入すると、25.12秒＝2.5×10¹秒となります。

※　なおこの計算については、当初解説に誤りがありました。N先生からの指摘があり、ぼくがはじめに計算をしたときには向心加速度の条件のみで計算をしていました。またN先生からのご感想で、

『aに1.6m/s²を、rに400mを代入すると、v=25.2m/sとなります』の記述は電卓だからできる計算で、手計算の受験生にｖを求める余裕はないと思います。まずはそのまま25m/sを使ってAB間の所要時間200π/25＝25.12を求めて①②③を答え、向心加速度を計算して25×25/400＝1.562から④⑤⑥を答えるので精一杯だろうと思います。

問２

この問題は400mから100mへと小回りをするので、そのままでは向心加速度が大きくなり、制限値を超えてしまいます。ですので逆算をして、100mのカーブのほうを条件として、制限加速度の1.6で曲がっているというようにします。

よってまずはCに到達したときに、回りきれる速度を求めると、

となります。25[m/s]から√160[m/s]まで速度を落とす必要があるので、等加速度直線運動の時間の無い式を使うと、

(√160)²−25² = 2(−２)ｘ

これをｘについてとくと、116[m]となります。よって1.2×10²を選びます。

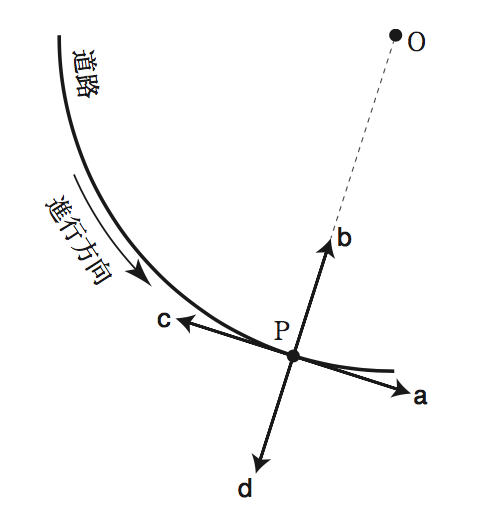
問３

減速をしながら（接線負の方向に摩擦力）、円運動（円の中心方向に向心力）するということで④を選びます。

B

問４

表１を見ると、

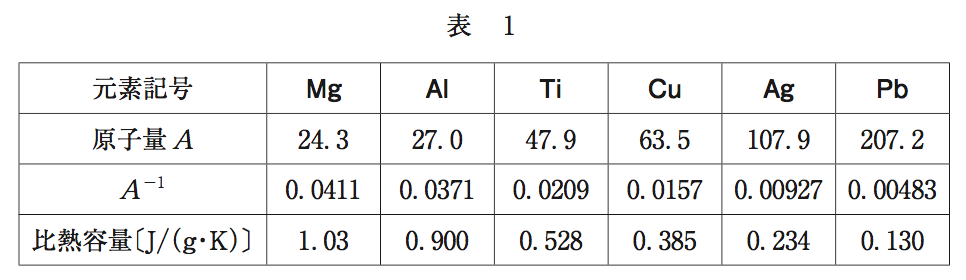
比熱容量が原子量が増えると小さくなっていくことがわかり、選択肢①を選ぶことができます。次に選択肢②と③では原子の数とエネルギーについて述べているのがわかります。このあたりは高校の教科書にもおそらく載っていないところですね。データから考えていきましょう。

各原子の比熱（１ｇ、１K上昇させるのに必要な熱量）[J/(g・K)]と原子量（１モルあたりの質量）[g/mol]をかけます。単位を計算してみると、

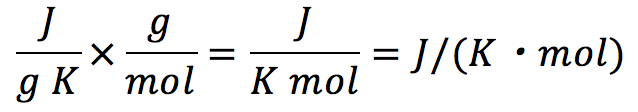
となっており、１モルあたり、１K上昇させるのに必要な熱量となり、比較をすることができます。表の中で原子量×比熱を計算してみましょう。例えばMg（マグネシウム）であれば、23.4×1.03= 24.1。同様にPb（鉛）であれば207.2×0.130＝26.9。このように見ていくと、各原子で値が25付近で一定になっているのがわかります。よって②を選びます。

##　感想

グラフ用紙を使っていいと問題文で書かれていますが、どのタイイングでどのように方眼用紙を使うと、より簡単に気がつけるのかがよくわかりませんでした。また、もしそうだとしても時間短縮にはならないのではないかと思うのですが…、何かアドバイスをいただけると幸いです。

追記

この問題に関しても、N先生からアドバイスをいただきました。グラフまでお送りいただき、僕自身グラフ用紙をどう使うのかがわからなかったのですが、よくわかりました。

『問4の表から1モル1K上昇させるのに必要な熱量の平均値を求める』とありますが、手計算でいくつかの3桁×3桁の計算をして平均が25と出し、その上で鉄の原子量55.8で割るのは大変です。受験生は電卓を使うわけにもいきません。

　ここでグラフを使えるかが運命の分かれ道と思います。私はこのテストを解答した最初には何も考えずに原子量と比熱の関係をプロットして線で結び、原子量55.8のところから比熱0.44を得ました。

　後から気がついたのですが、MgとPbではＡ-1が0.411と0.00483、比熱が1.03と0.130になっているのでともに約1/10の違いで、比例に近いと思いました。グラフを描くなら増加ー減少となるグラフより増加ー増加(減少ー減少)となるグラフの方が使いやすそうです。

問５

問題を解く際に、力学的エネルギーと熱エネルギーの数式を作りますが、鉄の比熱が書かれていないために計算をすることができません。そんな馬鹿な！どこかに書いてあるのではないか？と問題文を何度も読み直してしまいました。

ただし、問４のことを使えば、鉄の比熱については逆算して求めることができるということに気が付きました。面白い問題ですね。

まず問４の表から１モル１K上昇させるのに必要な熱量の平均値を求めると、およそ25[J/(mol・K)]となります。これを鉄の原子量の55.8[g/mol]で割ると、鉄の比熱0.450[J/(g・K)]と、求めることができます。これを使って力学的エネルギーが熱に変換されたとすると、

1/2×1000×20² [J]= m×0.45×160 [J]

m = 2777[g]

　となり、mを求めることができます。なお、mは比熱の単位の関係から[g]で出てきてしまので、最後に[kg]に直すために1000で割ることを忘れないようにしましょう。この中で選ぶとすると、3.0×10⁰[kg]となります。

問６

これは熱力学第二法則に反している、②を選ぶ必要がありますね。どのようにしても「熱」となって出ていってしまう部分がでてきます。

第３問の全体の感想

「ねらい」の記述を見ると

平面内を運動する物体の運動についての理解と，物理基礎で学習した運動・位置エネルギーや熱現象とエネルギーの関係に関する理解を基に，自動車を題材として，資料に示された条件を解釈し，グラフを活用・分析したり情報を統合したりするなど，課題を解決する力を問う。

と書かれています。

たしかにA問題については計算問題が多く、従来型の勉強方法で対応できます。対してB問題については、表の読み取りや単位を考える問題が多く「電卓」があるといいのですが、計算的にはかなり時間がかかってしまうのではないかと思いました。

今までのセンター試験では計算問題については負担が少ないように設問されていましたが、今後はそうではないということでしょうか。問５についてはざっくりとした計算でも求まるので、ざっくり計算の技も身につける必要がありそうです。

私大の個別入試や東工大・東大の問題に近いような作問だと感じます。生徒にとってはかなりの難問で、今までのセンター試験でも最高レベルの問題なのではないでしょうか。

第４問

問１

グラフを選ぶさいには、

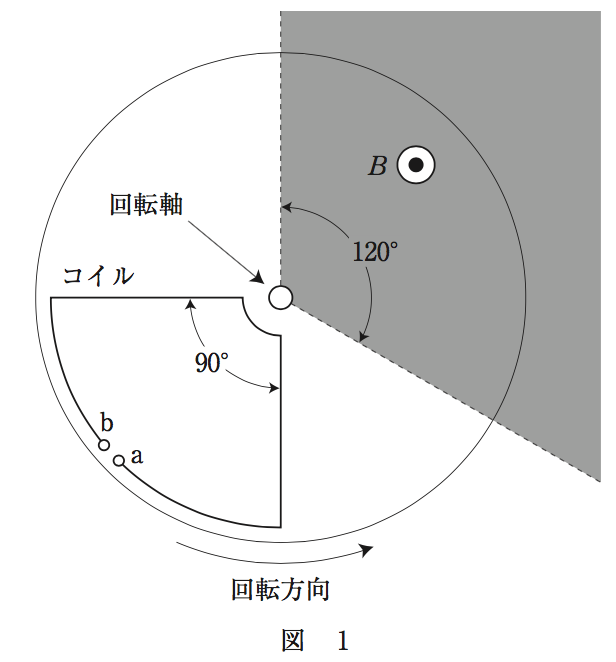
はじめは磁場中にコイルが入らないので、電位は０[V]（①）、

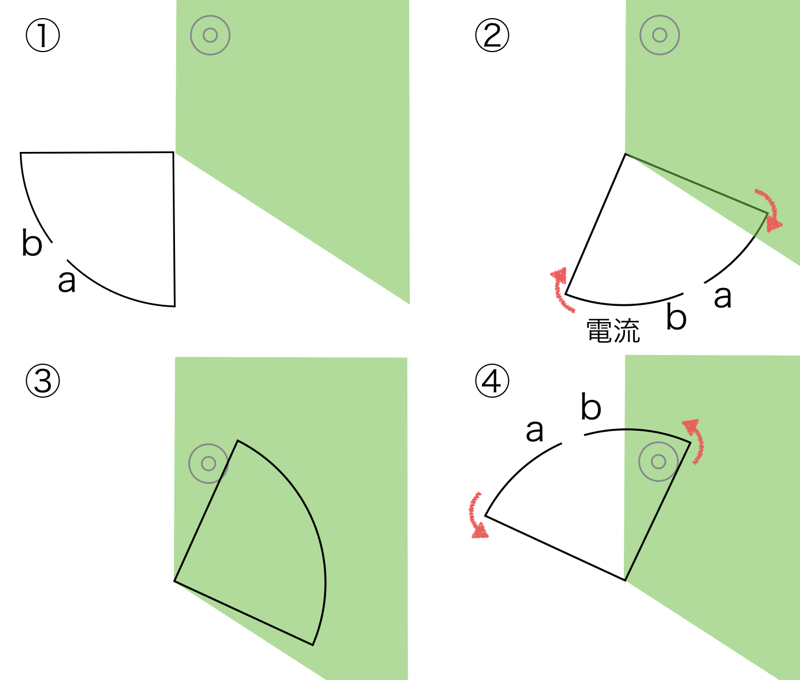
次に磁場中に入るとaのほうの電位がｂよりも高くなるので、負の方向にいくものを選びます（②）。そしてコイルが磁場の中に全部入るとコイル内の磁束が一定になるため、Vは０になり（③）、しばらくするとコイルがまた磁場中から出てくるので、今度は逆向きに電位が出ます（④）。このことから選択肢⑥を選びます。

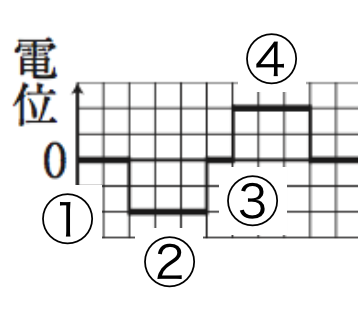
　また選択肢⑥のグラフをみると、はじめに３メモリ誘導起電力が発生しています（上の図②の部分）。この時間３メモリの中でコイルがすべて磁場中に入っていったと考えることができるので、

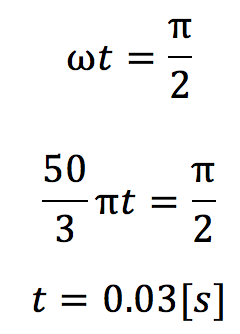
となり0.03秒に対応することがわかります。３で割ると、0.01秒となります。答えは②。

問２

ファラデーの電磁誘導の法則で考えていくと、

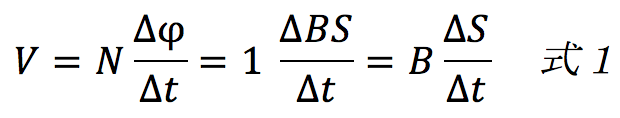
となり、ΔSが必要となります。

ある時間Δｔでコイルが磁場の中に入る面積ΔSは、

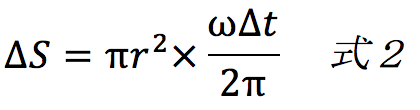
となります。ここでｒを扇形コイルの半径としました。問題文ではコイルの面積S’が出ているので、

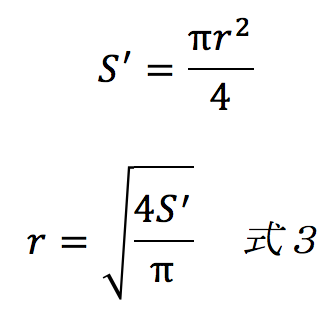
ということになります。

これらの式から、式１と式２より

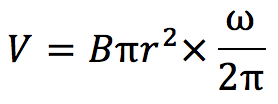
式３をrに代入すると、

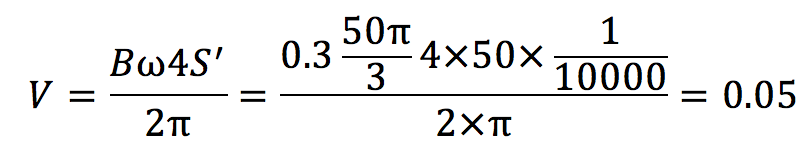
となります。単位に気をつけながら数値を代入していくと、0.05[V]となります。

第４問の早解き技

宮脇隆志先生からこの問題の早解き技をメールにて教えていただきました。

　問1のグラフを用いると分かりやすいと思いました。

　時間軸の3目盛りで0.03秒で，この間に扇形のコイル(面積50cm^2)がすっぽ り入り誘導起電力が発生することから，

ΔΦ＝BΔS＝0.30×50×10^(-4)，Δt＝0.03

　を用いると，簡単に計算できました。

第４問の感想

問題としては一般的なものですが、今までのセンターよりは難しい問題、リードαでいうと発展問題にあたるものになります。電磁気学の問題で、問が１・２しかなかったので、ウェイトとしては小さくなっています。

以上です。みなさんはどうお感じになりましたか？もし感想等がございましたら、ぜひ教えてください(^^)

センター試験の解説に戻る

科学のタネを発信中！

ニュースレターを月１回配信しています。

[subscribe2]

フェイスブックページ（科学のネタ帳）の登録はこちらから

@kuwakoさんをフォロー