テーブルクロス引きからロケットまで!驚きの「運動方程式」の世界
サイエンストレーナーの桑子研です。毎日が実験。

運動方程式 ma=F
ニュートンの三つの法則
「ma = F」。この数式、どこかで見た覚えはありませんか?これは運動方程式と呼ばれ、高校物理で最も有名な公式の一つです。
「力」という言葉は日常的に使いますが、では「力」とは一体何でしょう?例えば、小さな子どもに「力」をわかりやすく説明できますか?これは、私が授業で最初に生徒に問いかける質問です。実は、形のない「力」を言葉で説明するのは意外と難しいのです。しかし、この運動方程式は、まさに「力とはこういうものだ!」と定義するために作られた式なのです。
想像してみてください。スケートリンクで、いたずら好きのあなたが子どもの背中を「ドン!」と押します。すると、子どもは押された方向にスーッと動き始めますよね。これは、あなたが「力」を加えたことで、子どもの速度が変化(加速)したことを示しています。運動方程式の右辺「F」は加えた力を、左辺の「a」は加速度を意味します。つまり、運動方程式は「力とは、物体を加速させる能力のことである」と定義しているのです。
この式には、力「F」以外に「m」という記号もついています。「m」は質量を表しています。なぜ質量が関係するのでしょう? 同じスケートリンクで、今度は子どもではなく、より重い大人を押してみましょう。子どもよりも勢いがつきにくい、つまり加速しにくいことが分かりますね。これは、加速度「a」と質量「m」が反比例の関係にあるからです。
運動方程式(ma = F)を加速度(a)について解くと、以下のようになります。
この式を見れば、質量(m)が分母にあるため、質量が大きいほど加速しにくくなることが一目瞭然ですね。
力の単位、ニュートン
私たちは日常生活で、力の大小を感覚的に理解しています。しかし、感覚は人それぞれなので、正確に比較することはできません。そこで物理学の世界では、運動方程式を使って力の大きさを定義しました。
1 N(ニュートン)とは、1 kg の物体を 1 m/s² の加速度で動かすために必要な力と決められています。
この「ニュートン」という単位を、感覚として覚えておくことが大切です。身近なものを例に挙げてみましょう。
- 10 N(ニュートン):牛乳パック(1 kg)を手に持ったときの重さが、およそ10 Nに相当します。
- 1 N(ニュートン):約100 g の単一乾電池を手に乗せたときに感じる力が、およそ1 Nに相当します。
宇宙の不思議を解く、運動方程式の使い方
■ 力のつり合い
机の上に置かれたリンゴには、重力(W)と垂直抗力(N)という二つの力が働いています。垂直抗力は聞きなれない言葉かもしれません。床の上に長時間立っていると足が痛くなりますよね。これは、床があなたの体重を支えるために、上向きの力を加えているからです。この力が垂直抗力です。リンゴも私たちと同じように机の上に「立っている」ので、垂直抗力を受けています。
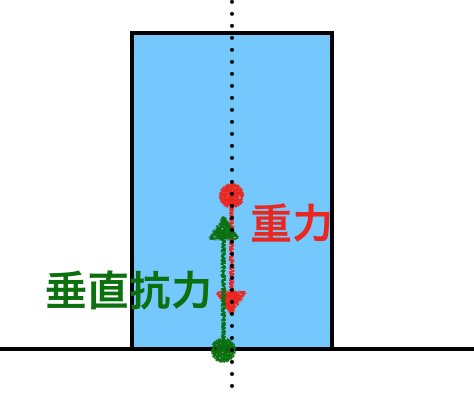
運動方程式を使って、この二つの力の大きさを考えてみましょう。机の上のリンゴは静止しています。つまり、加速度(a)は 0 です。運動方程式に a = 0 を代入すると、
となります。しかし、これは「リンゴに力が働いていない」という意味ではありません。運動方程式の「F」は、実は「働いているすべての力を合わせた結果」、つまり「残った力」を示しています。F = 0 ということは、「リンゴに働く力がこのとき打ち消し合って残っていない」ということを意味します。
このことから、重力と垂直抗力の大きさが同じであることがわかります。
同じ大きさの力が上下で打ち消し合い、結果的にゼロになったのです。これを「力のつり合い」といいます。静止している物体は加速度がゼロなので、必ず力がつり合っています。
同じように、もしこのリンゴを水に入れたとき、リンゴがぷかぷかと浮いて静止していたとしましょう。静止しているため、力はつり合っているはずです。しかし、床の上ではないので垂直抗力は働きません。重力は地球上ならどこでも働くので、下向きにリンゴを引っ張ります。では、このとき、重力とつり合う上向きの力は何なのでしょうか?

答えは浮力です。水の中では、物体は水圧によって生まれる上向きの力、浮力を受けます。力のつり合いから、リンゴの重力が1 Nなら、浮力も1 Nになります。
「静止している物体には、必ず重力を支える何らかの力が働いている」。そんな目で周囲を見渡すと、さまざまな力が見えてきて面白いですよ。
実は、静止していなくても力がつり合っている場合があります。加速度がゼロのとき、静止以外の状況を想像してみてください。
加速度が 0 とは、速度が変化しない運動のことです。つまり、物体が同じ速度で動き続けている場合も、力の合計はゼロになります。たとえば、カーリングのストーンは氷の上をスルスルと等速で進み続けます。このとき、ストーンには重力と垂直抗力以外の力はほとんどなく、力の合計はゼロになっています。
こちらは手作りをしたホバークラフトの様子です。
このように、物体は力が働かなければ、最初に持っていた運動をそのまま続けます。この性質を「慣性」といいます。静止状態は、速度がゼロの等速運動と考えることもできます。
■ 力がつり合わない場合
では、カーリングのストーンを氷の上ではなく、じゅうたんの上で滑らせたらどうなるでしょう?当然、速度はすぐに落ち、やがて止まってしまいます。
運動方程式(ma = F)をもう一度見てみましょう。aは加速度、つまり速度の変化です。じゅうたんの上ではストーンが減速している、つまり加速度は左を向いています。したがって、力が左側に残っていることになります。このとき、ストーンにはどんな左向きの力が残っているのでしょうか?
もうおわかりですね。その犯人は摩擦力です。摩擦力「f」が左側に働くため、ストーンは速度を落としていくのです。
もし摩擦力がなければ、どうなるでしょうか?物体に力が働かない場合、減速することはできません。ストーンは、最初に滑らせた速度のまま動き続けます。宇宙空間を永遠に飛び続ける彗星も同じ原理です。エンジンがないのに動き続けるのは、宇宙には摩擦力や空気抵抗といった運動を妨げる力がないからです。
ニュートンがまとめた三つの運動法則
科学者ニュートンは、力と運動について三つの法則をまとめ、「運動の法則」としました。
紀元前の学者アリストテレスは、物体の自然な状態は静止であり、運動を続けるには常に力が必要だと考えていました。これは「放っておけば物は止まる」という私たちの感覚と一致する考え方です。しかし、それから1700年後、イタリアの物理学者ガリレオ・ガリレイが「それは違う!」と異論を唱えました。
ガリレイは、「空気抵抗や摩擦力がなければ、物体は速さを変えずに動き続ける」と考えました。この考え方をニュートンは「慣性の法則」、つまり運動の第一法則としました。
運動の第二法則は「運動の法則」と呼ばれ、これがまさに運動方程式(ma = F)のことです。アリストテレスとは違い、「力」と「加速」を関連づけている点がこの法則の核心です。
そして、運動の第三法則は「作用・反作用の法則」といいます。例えば、いたずら好きな幼稚園児Aが、別の園児Bに頭突きをした場合を考えてみましょう。
頭突きされた園児Bが痛くてたんこぶができるのは当然ですが、頭突きをしたAにも同じようにたんこぶができます。このように、物体同士が力を及ぼし合うときには、必ず力のペアが現れます。このペアを「作用力」と「反作用力」と呼び、この二つの力は大きさが同じで、向きが反対になります。
こちらは無重量空間での作用反作用の様子です。
私たちは日常生活で、作用・反作用の法則を無意識のうちに利用しています。水泳のターンでは、壁を力強く蹴ることで、その反作用力を利用して反対方向へと進みます。また、ペットボトルロケットは、内部の水を後ろに噴出することで、その反作用力によって前向きの推進力を得ています。宇宙へ行く本物のロケットも同じ原理で、ガスを後ろに噴射し、その反作用力で加速しているのです。
作用・反作用の法則をうまく活用すれば、500mlのペットボトル2本で30mも飛ぶロケットを簡単に作ることができます。
■ 慣性とテーブルクロス引き
大工さんが使う「かんな」の刃を抜くとき、大工さんはかんなの台を金槌で叩きます。刃を抜きたいのに台を叩くのはなぜでしょう?
質量は物体の「動きにくさ」、つまり慣性の強さを示しています。質量の大きな金属でできた刃ではなく、質量の小さな木の台を叩くことで、同じ力でも台だけを急激に動かすことができます。そうすると、台に残ろうとする慣性のおかげで、刃がゆるんで抜けるのです。
また、ワイングラスが乗ったテーブルクロスを勢いよく引いても、グラスが倒れずにその場に残る大道芸をテレビで見たことがあるでしょう。これもグラスの慣性を利用した芸です。テーブルクロス引きやだるま落としも、物体の慣性という性質をうまく利用したものです。
※ この記事は拙著『大人のための高校物理復習帳』の付録記事として書いています。たの記事についても読めますので、こちらからどうぞ。
【特設ページに戻る】
『大人のための高校物理復習帳』(amazonリンク)
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!



