失敗しないテーブルクロス引きの研究：物理学的コツと理論と実際のズレ
サイエンストレーナーの桑子研です。毎日が実験。
物理の授業で行うと大盛り上がりの「テーブルクロス引き」。サッと引いたクロスの上の食器が、まるで魔法のようにその場に留まる様子は圧巻です。「失敗したら大惨事…」とハラハラするこの技、実は手先の器用さや運動神経だけで決まるものではありません。成功の裏には、れっきとした物理学の法則が働いているのです。なぜ食器は倒れないのか？どうすれば成功するのか？科学の視点から、テーブルクロス引きのコツを物理学的に解き明かしていきましょう。
テーブルクロス引きには物理がギュッと詰まっている、とっても興味深い題材なのです。
成功の鍵は「慣性」と「摩擦」
テーブルクロス引きを成功させるためには、２つの科学的な現象を理解することが重要です。
・食器がその場に止まり続けようとする性質（慣性の法則）
・クロスが食器を横に引っ張る力（動摩擦力とシワの抵抗力）
この２つの戦いによって、物体の動き方が決まり、テーブルクロス引きでの物体の動き方と成否が決まります。
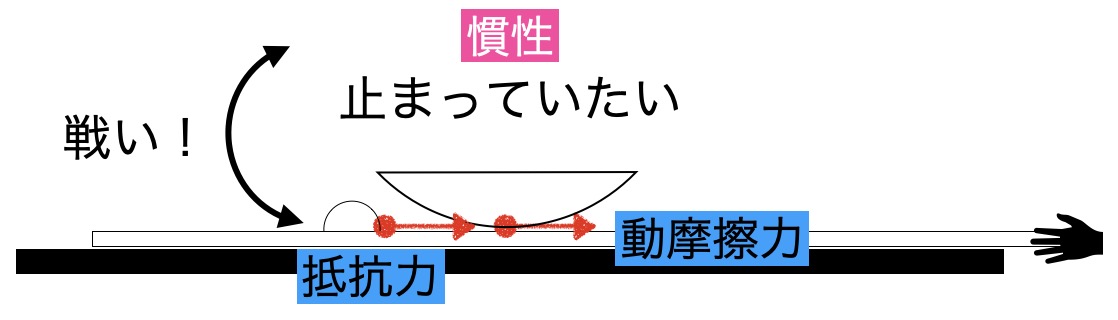
まず、１つ目の「慣性」。これは、中学校の理科で習う「運動の第１法則」のことです。「止まっている物体は、外から力を加えられない限り、ずっと止まり続けようとする」という性質です。 急発進した電車の中で、体が後ろに持っていかれる感覚、あれがまさに慣性です。テーブルの上の食器も同じで、「ここに止まっていたい！」と頑張っているのです。
次に、２つ目の「動摩擦力と抵抗力」。クロスを引くと、クロスと食器の底がこすれ合います。この時、クロスが食器を「一緒に動こうよ」と引っ張る力が生まれます。これが摩擦力です（静止摩擦力・動摩擦力）。後述しますが、このほかにクロスのシワがぶつかる力も加わります（この記事ではこれをシワの抵抗力と呼びます）。
つまり、テーブルクロス引きとは、「止まっていたい食器の気持ち（慣性）」と、「クロスが引っ張る力（摩擦力）＋シワの抵抗力」のせめぎ合いで成功が決まるのです。
全ての物体が慣性という性質（今の動きを保とうとする性質）を持っていることを、慣性の法則と言います。ニュートンはこれを運動の第一法則としました。慣性の法則は日常生活でも感じることができます。
例えばバスや電車の中で立って吊り輪を持っている時、バスが急発進すると、体が元いた場所に止まろうとするので、体が傾きますよね。これは静止したものは静止を続けるという慣性のためです。また動いているバスが急ブレーキをかけた時、体は今までは運動をしていたので、その方向に飛び出ますよね。これは運動していたものは同じ運動を続けるという慣性の一つです。 詳しくはこちらの記事もご覧ください。
だるま落としも面白い遊びですね。あれも慣性の面白さを感じるおもちゃですが、下のパーツをハンマーで叩くと、上のパーツは静止をしていますから、静止を続けようとしてそのまま下に落ちてきます。まただるま落としは実は質量の大きなものの方が成功しやすいです。これは慣性が大きくなるためですね。こちらにだるま落としのコツを書いたのでご覧ください。
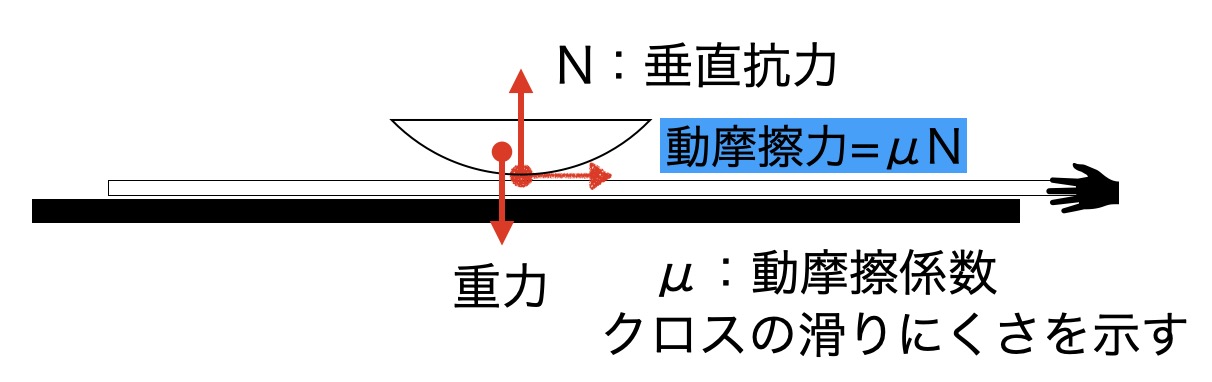
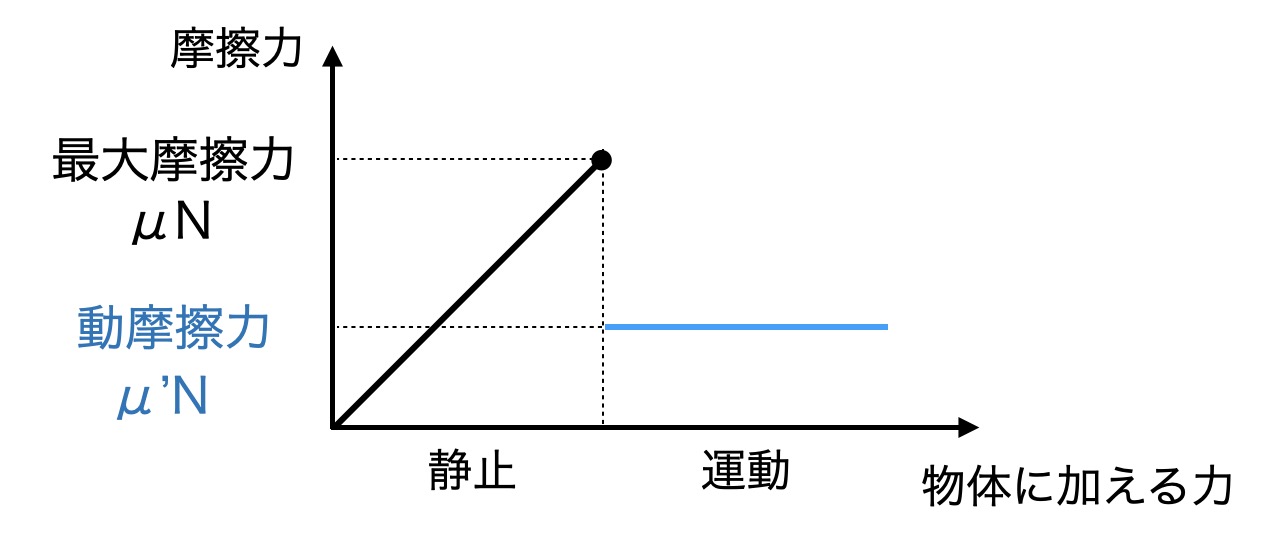
次に摩擦力を詳しく見てみましょう。摩擦力は動摩擦係数と垂直抗力の積で表されます。摩擦力係数はクロスとお皿の素材で変わるもので、クロスだけで言えば、滑りにくさを示します。摩擦係数が小さいほど、ツルツルしていて、お皿はその場に止まりやすくなります。テーブルクロスを引くときに、お皿と生地が一緒になって動きときには静止摩擦係数が、その後すぐにずれ始めますが、この時は動摩擦係数が働きます。次の図は動摩擦力の関係を示しています。
実際にテーブルクロスひきを行ってみました。こちらの動画をご覧ください。質量を変えて実験をしました。
摩擦ですが、どんなすべすべしたものにも働きます。ミクロに見れば、その表面は凸凹しており、その凹凸同士がかみ合わさって摩擦が生じます（なお、摩擦力が働く原因はその他の原因もありますのでご注意ください）。
なぜ「スピード」が命なのか？物理学が明かす秘密
実は、クロスが動いている時に食器に働く摩擦力（動摩擦力）は、どんなに速く引いても、ゆっくり引いても、力の大きさ自体はほとんど変わりません。「えっ、速く引いた方が摩擦が大きそうだけど？」と思いますよね。でも、物理学的には、動摩擦力は「物体の重さ」と「接触面の滑りにくさ（動摩擦係数）」で決まり、接触面の大きさにも、速さには依存しないのです。
では、なぜ速く引く必要があるのでしょうか？それは、摩擦力が働いている「時間」が重要だからです。食器がどれくらい動いてしまうかは、「加えられた力」と「力が働いている時間」によって決まります。 ゆっくり引くと、弱い力であっても、長い時間食器を引っ張り続けることになります。その結果、食器はだんだん加速して動き出し、最後には倒れてしまいます。
逆に、一瞬でサッと引けば、食器がクロスから引っ張られる時間はごくわずかです。 摩擦力が働く時間を極限まで短くすることで、食器が動き出す暇を与えず、まるでその場に止まっているように見せることができるのです。これが、「スピードが命」と言われる科学的な理由です。
実践！物理法則を味方につけるコツと準備
理論が分かったところで、具体的な成功のコツと準備を見ていきましょう。
その１ クロスのセッティングを工夫する
準備の段階で勝負は半分決まっています。クロスを完璧にセッティングする テーブルにピッタリと敷き（両端から引っ張るなどして）、空気を抜いて、シワが全くない状態にします（このシワが大きなポイントになります）。アイロンをかけておくのも効果的です。これはシワの抵抗力をできるだけ小さくするための工夫です。またシルクの布のような、ツルツルした滑らかな素材を選びましょう。これは動摩擦係数を小さくし、食器を引っ張る摩擦力そのものを減らす効果があります。縁の刺繍や縫い目などの引っ掛かりもないものの方が良いです。
その２ とにかく「圧倒的なスピード」で引く
これが最も重要です。ためらってはいけません。前述の通り、動摩擦力が働く時間を少しでも短くするため、一気に引き抜きます。
その３ 引く方向は「斜め下」（45度くらい）
クロスを上に持ち上げるように引くと、クロスの下に空気が入り、しわが生じたり・食器が浮き上がってバランスを崩したり、結果として摩擦が増えたりして失敗の原因になります。 また、重要なのはできるかぎり引っ張る最中に「シワを作らないこと」。シワができると、それが食器に引っかかり、「小さな壁」となって食器を押し出してしまいます（シワの抵抗力が大きくなります）。 テーブルとクロスの間に余計な空気が入らないよう、真横か、少し斜め下に向かって引き抜くのがポイントです。
その４ 食器を重くする
意外かもしれませんが、軽いプラスチックのお皿などは、慣性が弱いためシワの抵抗力が生じた場合、簡単に動いてしまいます。そういった面では意外かもしれませんが、コップに水などを入れて重くすると、慣性がますので、成功しやすいのです（ただし重すぎると摩擦も増えるのでクロスを引く速度が遅くなってしまいます。バランスが大切です）。
また、重心が低く、底面が広いお皿の方が安定します。重心は低くしたいです。コップを使うなら、重心を下げるためにも水を半分以下に入れましょう。こうすることによって、質量が出たと同時に、重心はあまり高くなりません。
水を入れすぎると慣性は大きくなりますが、重心がその分高くなり、小さな傾きが起きても倒れやすくなってしまいます。
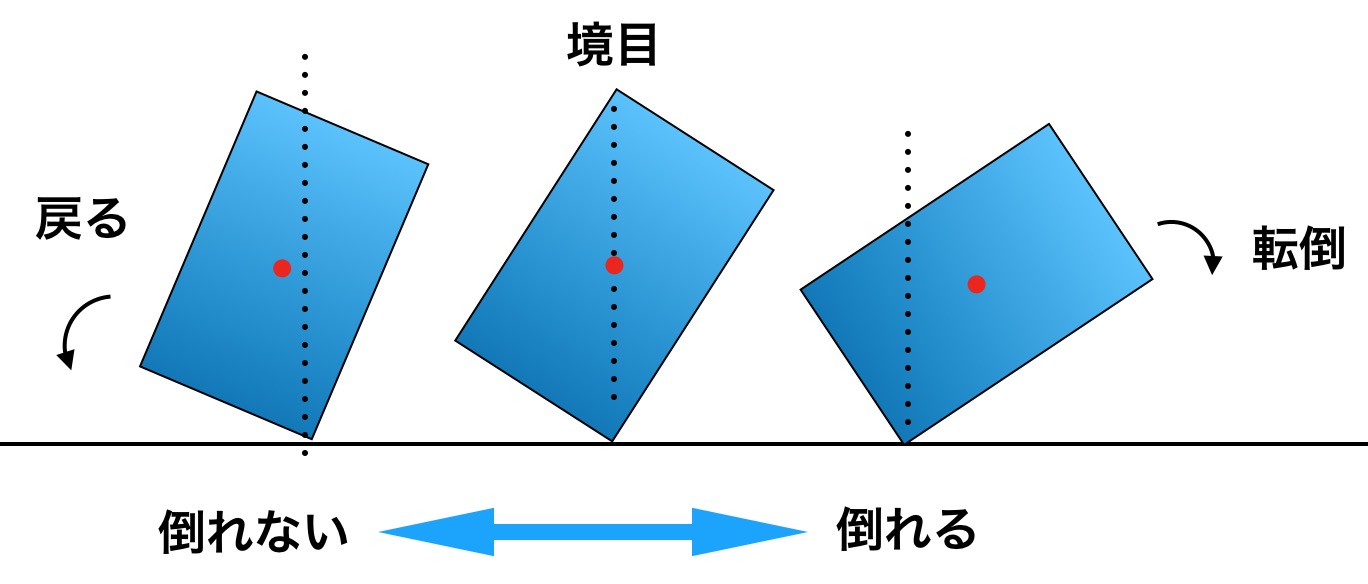
これが失敗の原因です。重心もとても面白い科学です。詳しくはこちらの記事をご覧ください。
そう考えると、最適なのは水を半分くらい入れた場合となります。
その６ 食器の配置
どんなに上手く引いても、シワの発生や摩擦力をゼロにすることはできません。最初からテーブルの端ギリギリに置くのではなく、できるだけ机の奥側に置くことで、落下のリスクを減らせます。
最終チェックポイント！ クロスのどこを持つのか？
これについては最重要なので、まとめて下に記載しますが、食器を置いた延長線上を持って引きます。
クロスの両サイドではありません。ここで実際に何が起こっているのか！物理的な理解がとても大切になるわけです。私もこの部分までは実際に動画を撮影して解析するまでは考えが及びませんでした。
驚きポイント！摩擦力と質量の関係
ここで気になることが一つ。テーブルクロス引きは、質量の重いもの（重い皿や食器）の方が成功しやすい、またはより動かずに済む傾向があります。これは、主要な物理法則である慣性の法則と摩擦力の観点から説明できます。
クロスを引く際に皿に作用する力は摩擦力Fです。摩擦力は皿の重さ（垂直抗力N=Ｍｇ）に比例します。一見すると、質量 m が増えると摩擦力Fも増えるため、皿は動きやすくなるように思えます。しかし、皿が動く際の加速度 a に注目すると、以下のようになります（ニュートンの運動方程式）。
m: 質量
μ’: 摩擦係数（皿とクロスの材質で決まる）
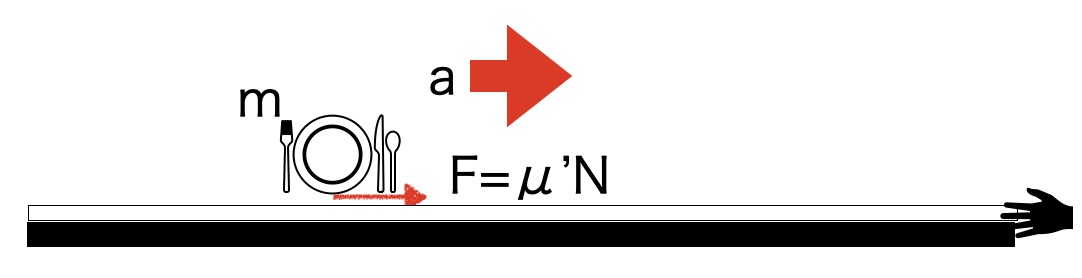
ma=F
ma=μ’(mg)
a=μ’g
この式が示す重要な点は、皿が受ける加速度 a は質量 m に依存せず、摩擦係数 μ’と重力加速度 g だけで決まるということです。つまり、重い皿も軽い皿も、クロスが接触している限りは同じ加速度で動こうとします。あれ動摩擦力には質量は関係ないの？なら質量はなんでも良いじゃないか？そう思いますよね。
ではなぜ質量が大きいと有利なのか？
摩擦の計算上、物体の質量は関係ありません。ただし実際問題やってみると、テーブルクロスを引き抜く際には、多少の衝撃や振動・クロスのしわがどうしても発生します。このシワが大問題です。こちらの動画をご覧ください。
失敗するパターンを解析すると、とにかくしわが問題になっていることがわかります。もともとシワのできている中央に置いた時には失敗します。
また別の場合でもしわがぶつかることがあります。どうしてもしわができてしまうことは避けられません。
こちらがうまく行った時の様子です。しわがあまりできていないのがわかりますね。
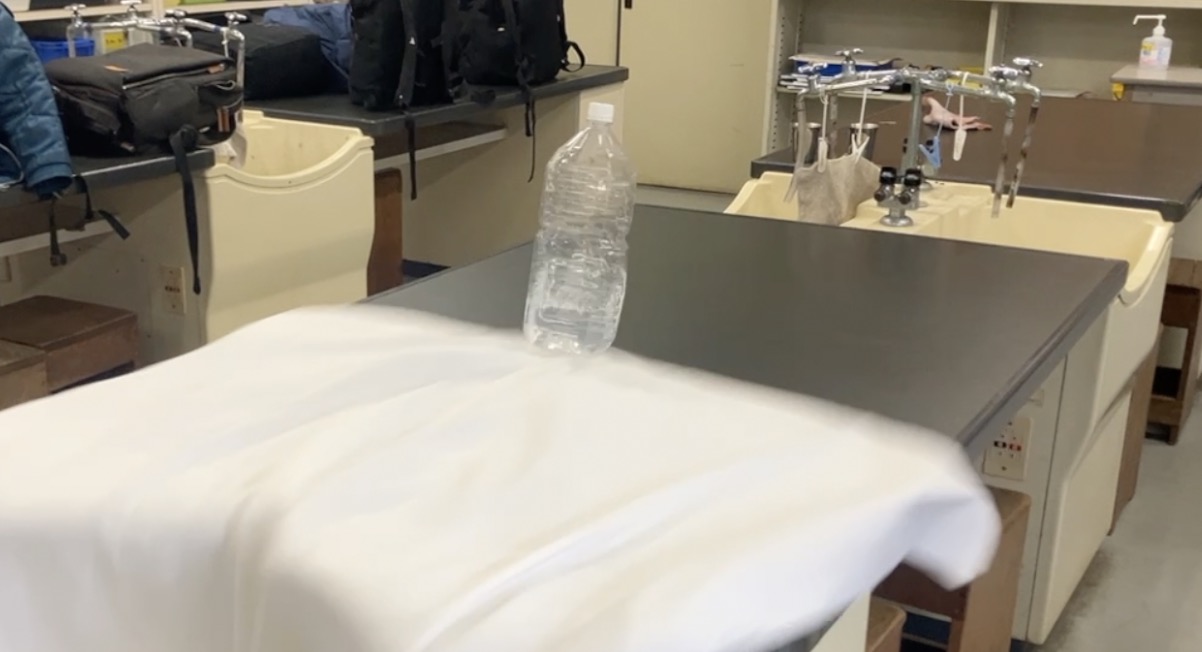
この時、質量が大きいと、慣性が大きく、静止を保とうとする性質が大きくなります。そのため実験的には、質量が大きい方が慣性が強くなり、結果として動く距離が短くなる傾向が強いと考えられます。
結論として、質量の大きな物体は静止を保とうとする慣性が大きく、小さな振動や乱れに対して安定しているため、シワの抵抗力にも動きにくくなります。
ただし、質量が大きいほど、動摩擦力は大きくなるため引き抜くための力（スピード）が小さくなってしまう可能性があり、そこが難しいところです。
シワによる抵抗力をできるだけ小さくするためのポイント
クロスを引く際は、持つ位置が重要です。こちらの動画をご覧ください。
何も考えないと（素人は）、クロスの両サイドを持ってしまいがちですが、ここでクロスが剛体（形が変わらない物体）ではないということがポイントになって、失敗してしまいます。映像を見るとわかりますよね。生地は少なからず伸びてしまうからです。
置いた物体（今回はペットボトル）の真下を引くと、しわはできにくくなります。
それに対して、両サイドを持つと、大きなシワが現れます。
このシワが食器等にぶつかって、シワの抵抗力となって、食器を押し倒してしまうわけです。なぜこのように大きなシワができるのでしょうか。試しに片手で引っ張ってみます（ましたに引っ張ります）。
すると、大きなシワができます。クロスが板のような物体であれば、変形をしないのでシワが起こり得ないのですが、生地は多少なりとも伸び縮みをします。つまりは、ペットボトルと生地の間で生地が伸びる部分と伸びない部分が生じ、伸びた部分が元に戻ろうとする力（弾性力）を四方八方にお呼びします。そのため周りの伸びていない生地の部分を引っ張り、伸びた記事の周りに大きなシワができてしまうのです。
両サイドを持った場合
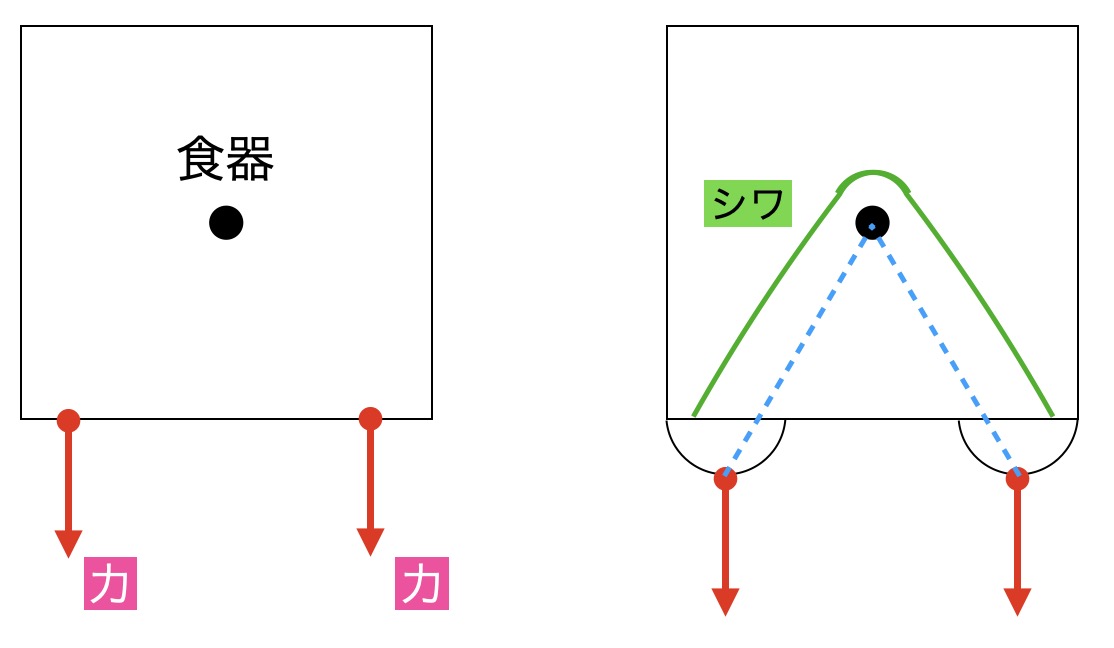
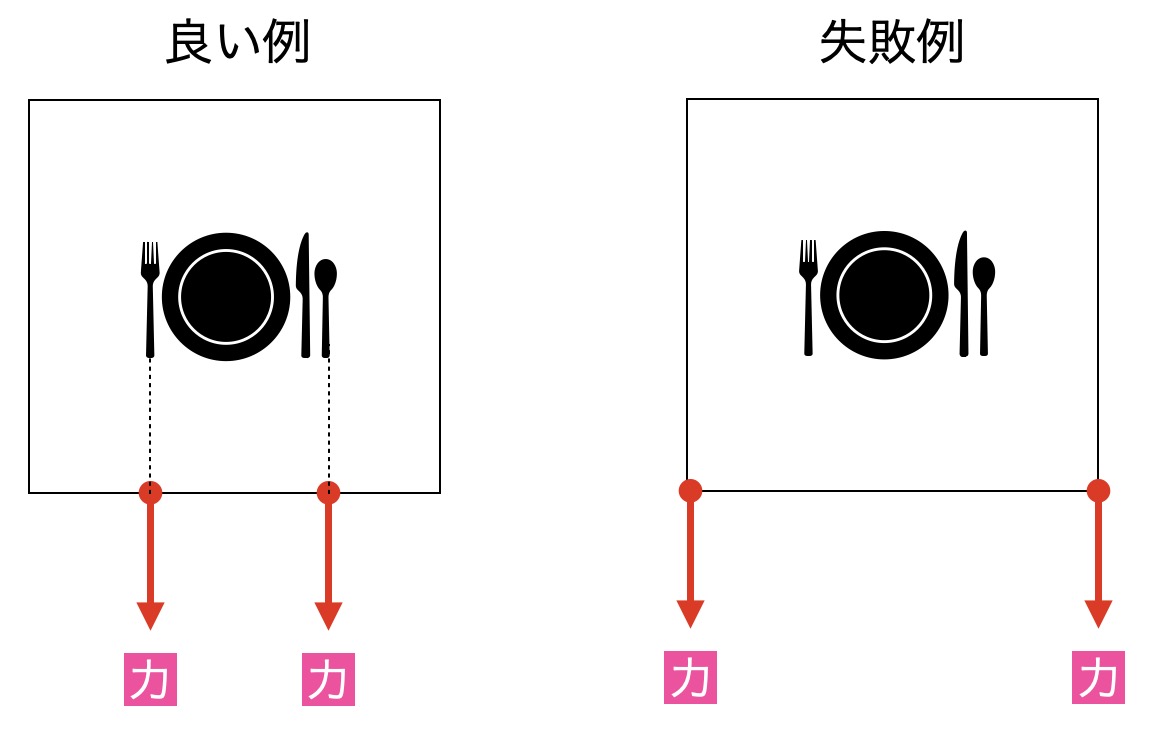
食器のある真下を持って引くことによって、伸びる方向が一直線になり、生地の弾性力もペットボトルと手の間での引っ張り合いになり、シワが食器の後ろ側にできにくくなると考えられます。
今回は質点として食器を考えてみましたが、大きさもあるので、置いた食器の幅に合わせて、その真下を両手で持って引き抜くということになります。
実際にやってみよう！テーブルクロス引きで食器はどの程度動くの？
実際に物理計算をしてみましょう。今回はしわの影響が全くなく、動摩擦直の影響のみで計算をしてみて、実際の現象と比較をしようと思います。理科室の机を使って実際に試してみました。
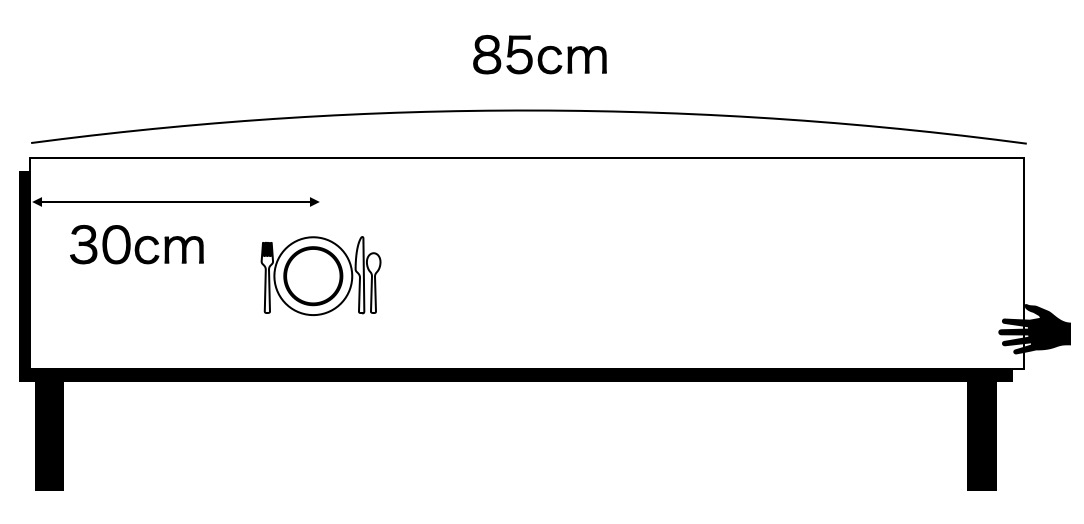
こちらがその実験動画です。テーブルクロスをひく前は奥から30cmの場所に置きました。テーブルクロスを引いたら、どこまで動くのか。実際に測ってみました。
結果、お皿は元の位置から8.4cm滑りました。お皿の質量は148gでした。
また動摩擦力はばねばかりで測定すると、0.48Nでした（ここから動摩擦係数を計算するとμ’=0.33）。
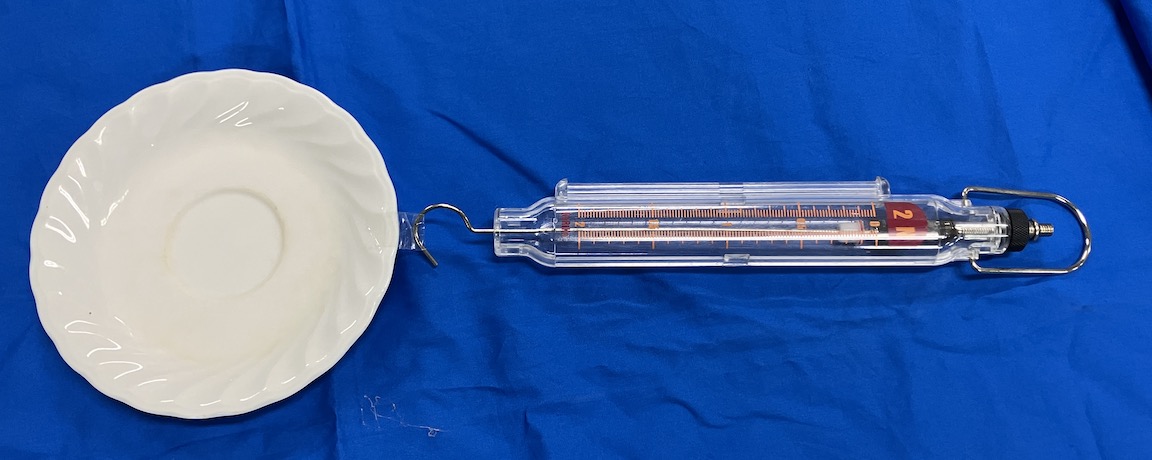
また机との動摩擦力は、測定すると0.50Nでした。
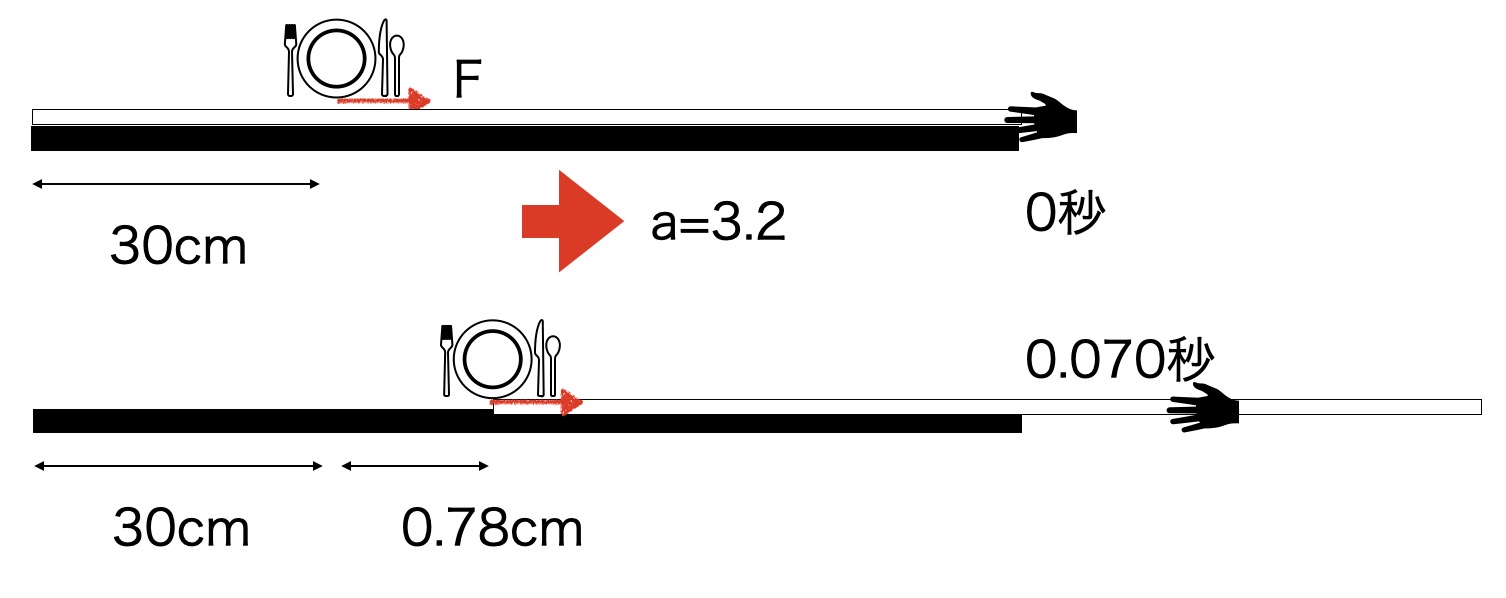
実際に、動摩擦力だけが働いた時に理論的にはどれくらい動くのかをざっと計算してみます（色々な仮定を含みます）。動画を解析したところ、テーブルクロスは机の端から端までを0.20秒で引き抜くことができました（ビデオ解析による）。
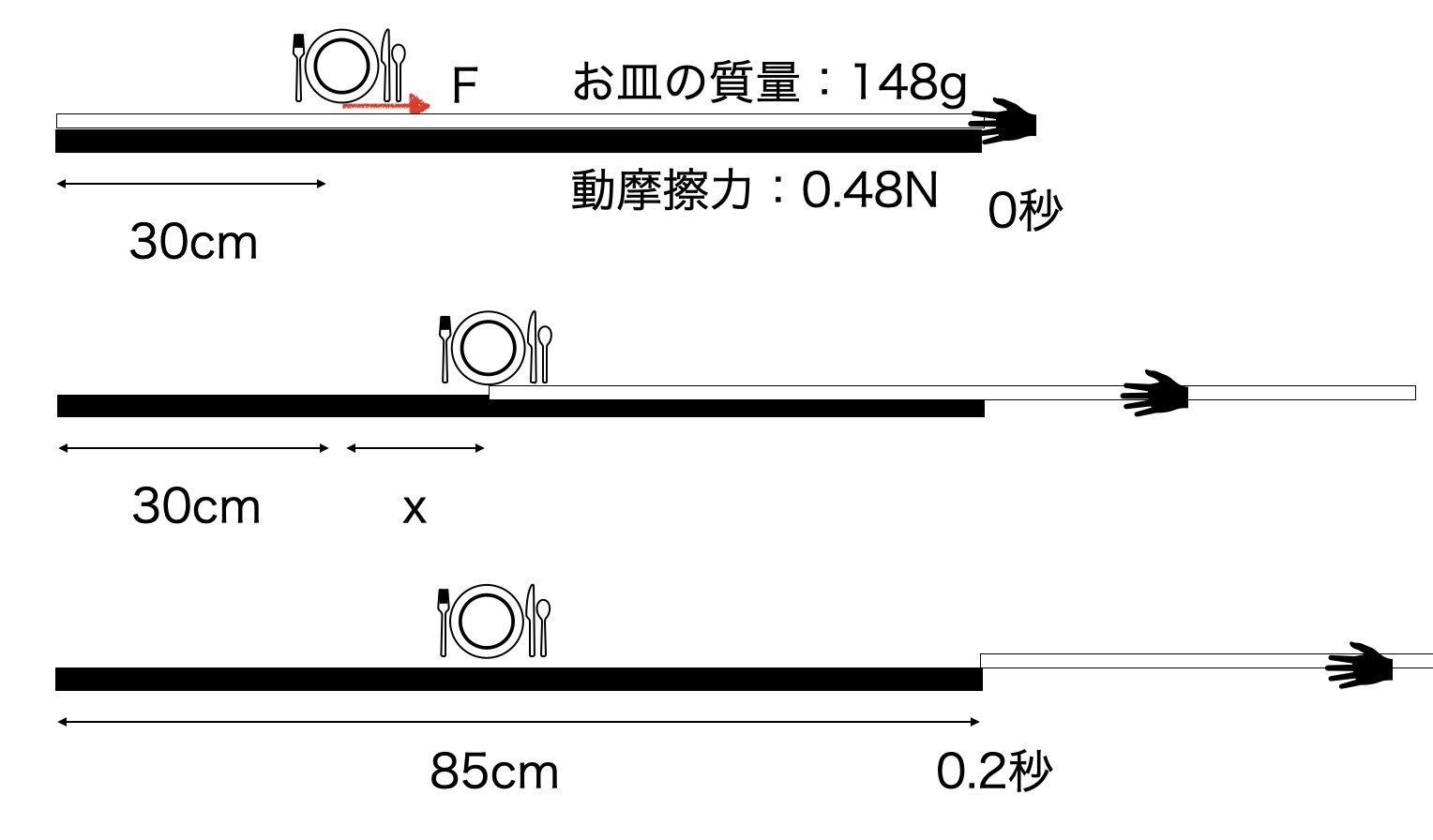
この時、テーブルクロスの速さが一定だと仮定すると、その速さは、v=x/t=0.85m/0.2s=4.25m/s(時速15.3km/h)となります。お皿を通ったクロスは30cmの部分なので、これを使うとお皿を通りすぎるまでの時間は、
t=x/v=0.30m / 4.25m/s = 0.070s
です。
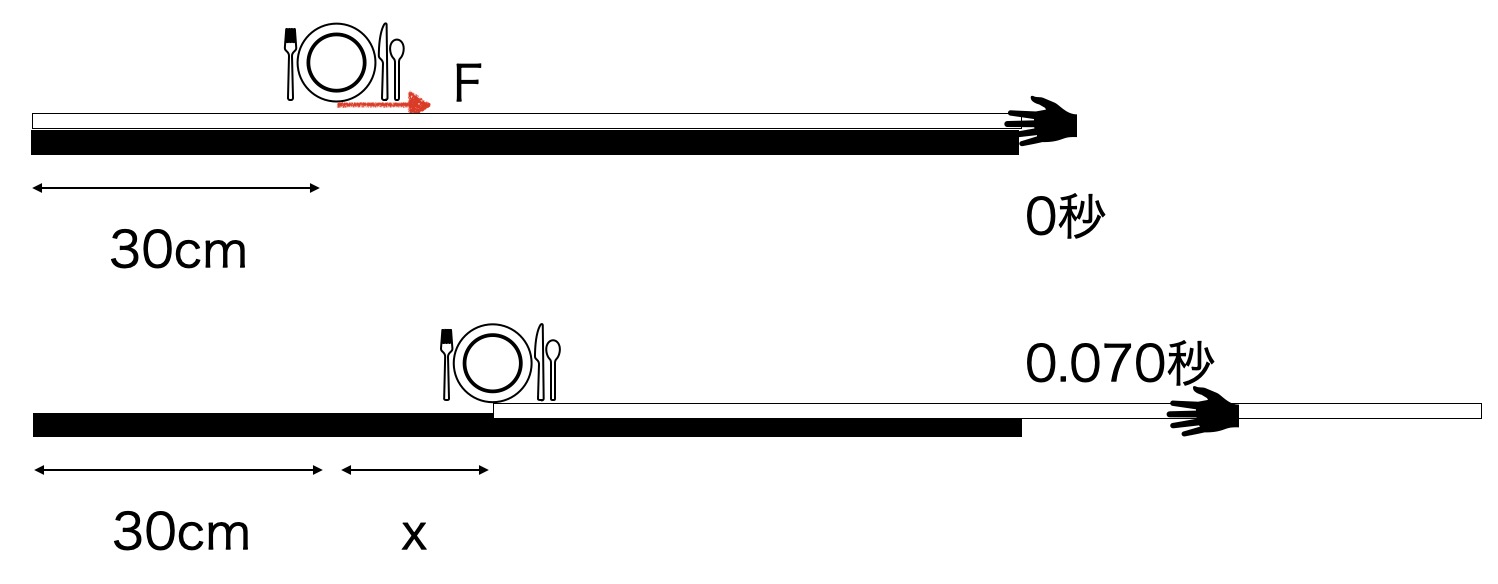
この間のお皿の加速度を求めます。動摩擦力は一定なので、運動方程式より、
ma=F
0.148[kg]×a=0.48[N]
a = 3.2[m/s^2]
ではお皿が動く距離を計算すると、
x = 1/2at^2=1/2×3.2×0.07^2 = 0.0078m = 0.78cm
となります。
またこのお皿は今度は速度がついているので、クロスが抜けた後は、テーブルの上を滑って止まります。止まるまでの距離を計算しましょう。まずどのくらいの速度をクロスがなくなるまでに持つのかを計算します。
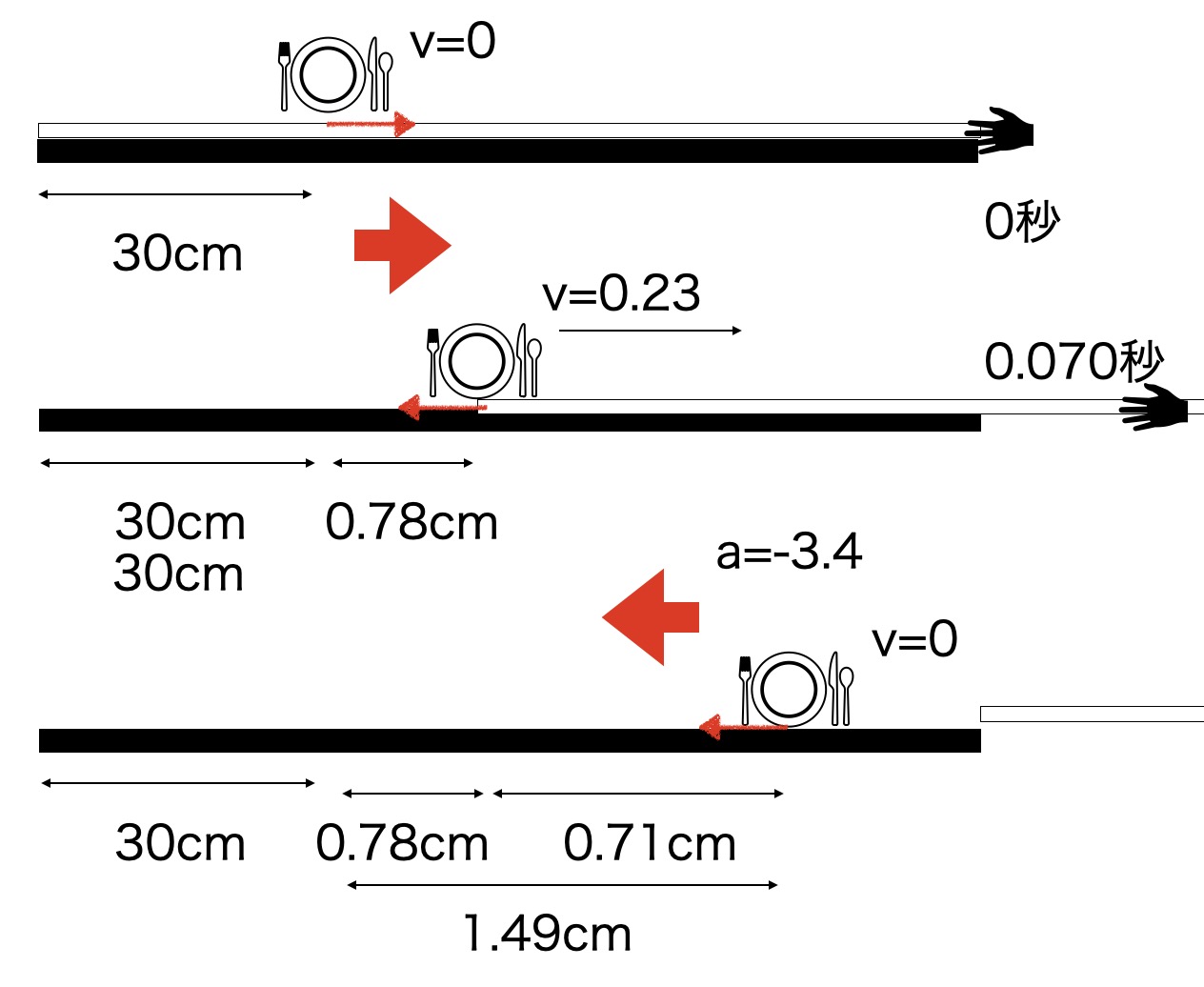
テーブルクロスを引くことでお皿が持つ速度は、
v=at=3.2[m/s^2]×0.070[s]=0.22[m/s]
また動摩擦は今度は机の摩擦力が必要になりますが、これはクロスとほとんど変わらずに0.50Nでした。よって、この時の加速度は
0.148[kg]*a=-0.50[N]
a=-3.4[m/s^2]
このことから止まるまでの距離はv^2-v_0^2=2axより
0[m/s]^2 – 0.22[m/s]^2 =2*(-3.4[m/s^2])*x
x=0.0071[m]=0.71[cm]
となります。結果として合計で、0.78+0.71=1.49cmとなりました。ただし実際に今回実験をして動いたのは8.4cmなので動きすぎです。これは動摩擦力以外の効果、つまりシワの抵抗力が大きそうです。シワや振動が発生することによって、お皿は影響を受けて滑ってしまうということが考えられます。
質量を大きくしてみよう！
摩擦力の影響のみの計算、つまり理論に近づけるためには、動摩擦力以外の効果が小さくなる必要があります。そこで質量を増やそうということになります。質量を増やしても動摩擦力は変化しないので、お皿の上にペットボトルを乗せてみました。
すると動く距離は断然変わりました。理論値（1.49cm）に近い数字になりましたね。
8.4cm → 3.3cm
これは慣性が大きくなった結果です。こう考えると、やはり質量が大きければ大きいほど、つまり重ければ重いほどシワなどの影響を受けにくく、動きにくいため、理論値に合ってくるということが考えられます。かといって、重ければ重いほど、クロスを引き抜く時間が増えてしまうため、その分動摩擦力が働く時間も伸びてしまいます。そのバランスを探るのが最適解となりそうです。
いかがでしたか？ 一見難しそうなテーブルクロス引きも、科学の法則を理解し、条件を整えれば成功率はぐっと上がります。 ぜひ、安全な場所で、割れても良い食器から練習してみてください。物理学を味方につけた見事な成功を祈っています！
また慣性の法則の概念は、日常に反しており、その理解は実はとても難しいのです。そんな慣性の法則や摩擦力についての普段から研究をしています。慣性の法則について深く理解することを目指した実践授業を開発しました。合わせてご覧ください。中学生・高校生どちらも楽しめる内容になっています。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
