【物理の謎解き】計算が楽しくなる!投げ上げ運動の3ステップ攻略法(物理基礎)
サイエンストレーナーの桑子研です。毎日が実験。
ビルの屋上からボールを真上に投げたら、一体どこまで上がって、いつ地面にたどり着くんだろう? そんな未来をピタリと予言できる「魔法の公式」があるとしたら、知りたくありませんか?物理学は、難しそうな数式ばかりの学問ではありません。実は、身の回りのモノの動きを解き明かし、その未来を予測するための、超強力なツールなんです。今日は、落下運動の問題を題材に、物理の公式という名の「魔法」を使いこなすための冒険に出かけましょう!
今回のミッション:投げ上げられたボールの運命を解き明かせ!
まずは、今回のミッション(問題)を確認しましょう。まるで探偵のように、与えられた情報からボールの未来を推理していきます。
【問題】高さ19.6mのビルの屋上から、小さな球を真上に速さ14.7m/sで投げ上げました。地球がボールを引っ張る力(重力加速度)は9.8m/s²とします。空気の邪魔は考えません。
(1) ボールが一番高い場所にたどり着くのは、投げてから何秒後ですか?
(2) そのとき、地面からの高さは何mになっていますか?
↓
さあ、謎解きの始まりです!
↓
↓
冒険の地図を描こう!攻略のための3ステップ
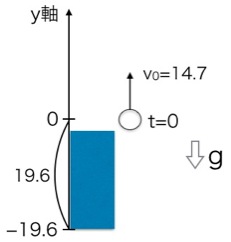
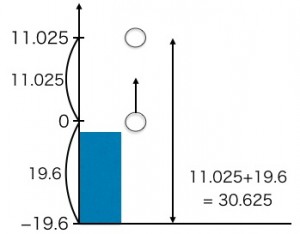
これが冒険の作戦マップです! 今回は、ボールを投げたビルの屋上を「スタート地点(原点 0)」にしました。ボールは最初に上に動くので、y軸のプラス方向は「上向き」と決めます。すると、地面はスタート地点より下にあるので、「-19.6m」の場所ということになりますね。
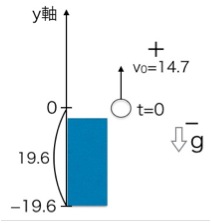
ステップ2:+と−の符号の確認
次に、軸の方向を見て、ボールに働く力に+か−の符号をつけます。
私たちが決めたy軸は「上向きがプラス」でした。ボールを最初に投げる速さ(初速度)は上向きなので、これは味方の力、「プラス(+)」です。一方、重力は常にボールを下に引っ張る敵の力。なので、重力加速度は「マイナス(-)」になります。この敵と味方の区別が、超重要です!
ステップ3:公式をカスタマイズ
基本の公式に、ステップ2で決めた符号を入れて、今回のミッション専用の公式に作り変えましょう!
基本の呪文(等加速度運動の公式)に、さきほどの味方の力(v_0=+14.7)と敵の力(a=−g=−9.8)を代入します。
いざ実践!ボールの最高到達点を探る
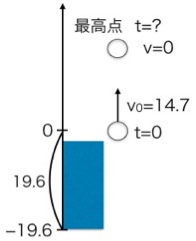
ボールが一番高い場所に到達した瞬間、上向きの勢いがなくなり、下に落ち始める直前に、一瞬だけピタッと止まります。つまり、最高点での速度 v は 0 なのです。これが最大のヒントです!
このヒントを速度の呪文 v=−gt+14.7 に使ってみましょう。「v=0」を代入すると…
0=−9.8×t+14.7
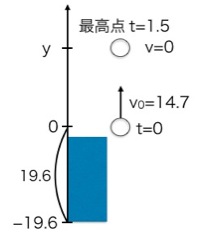
これを t について解くと、「t=1.5 秒」と出ました!これが(1)の答えです。ボールは投げてから1.5秒後に最高点に達する、と未来が予言できましたね!答えが出たら、書き込んでおきましょう。
次に、そのときの地面からの高さを求めます。位置の呪文に、先ほどわかった t=1.5 を代入します。すると、「y=11.025m」と計算できます。
ここで注意! この11.025mは、あくまでスタート地点(ビルの屋上)からの高さです。地面からの高さを知るには、ビルの高さ19.6mを足してあげる必要があります。
つまり、11.025 + 19.6 = 30.625 ≒ 31m。これが(2)の答え。
裏ワザ?時間を使わないショートカット公式!
この呪文は、時間を知らなくても、速さと距離の関係だけで答えが出せる優れもの。v=0(最高点)、v_0=14.7、a=−9.8 を代入すると…
0^2–14.7^2=2(−9.8)x
これを x について解くと、一気に x=11.025m が出てきます!あとはビルの高さを足すだけ。ね、便利でしょう?物理の公式は、ただ暗記するものではなく、状況に合わせて使いこなす冒険の道具です。この3ステップをマスターすれば、どんな落下運動の問題も怖くありません。さあ、次のミッションに挑戦してみましょう!
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!