落差16mの恐怖、理科で解明!スプラッシュマウンテンを数式でのぞく【ディズニーランド物理学】
サイエンストレーナーの桑子研です。毎日が実験。
あのスプラッシュマウンテン、実は理科で速度が求められるって知ってた?

「東京ディズニーランドのスプラッシュマウンテンに乗ったことがある人?」と聞くと、教室のほぼ全員が手を挙げる。生徒にとって東京ディズニーランドは、まさに“体験済みの物理ワールド”です。一方、「FUJIYAMAに乗ったことある人?」には、ぽつぽつと10%ほど。どうやら“絶叫”のハードルは高いようです。
でもちょっと待ってください。東京ディズニーランドで最も速い乗り物、それがスプラッシュマウンテンだということをご存じでしょうか? あの、丸太ボートで滝壺にダイブする、例のアトラクションです。
実はこのスプラッシュマウンテン、中学・高校の物理基礎の知識で、そのスピードを予測・計算することができるんです!もはや“遊び”ではなく“教材”――そんな目で、改めてスプラッシュマウンテンを見てみませんか?
実際どのくらいの高さ?――まずは基本データ

スプラッシュマウンテンの特徴的な落下シーン。あのクライマックス、どれくらいの高さから落ちているかというと…公式ガイドブックによれば、最大落差は16m。
つまり、校舎の3階分ほどの高さから水しぶきを上げて落ちていくわけです。スプラッシュマウンテンについて乗ったことがない方がもしいたら、こちらの動画の7分ころの様子をご覧ください。これが落差16メートルの滝です。
さらに調べてみると、以下のような公式データも得られました:

全長:850m
• 水量:毎分110トン
• 最大傾斜:45度
• 最高速度:62km/h
これらの数値は、物理好きにはたまらない“計算したくなる”数字ばかり。
実測データを取りに行ってみた
実際に自分で検証してみたくなり、修学旅行引率中の自由時間を使って、スプラッシュマウンテンに乗ってきました(乗り物が苦手なのでほぼ命懸けでした…)。
高度計と加速度センサーを忍ばせて、データ収集。結果として、落差はしっかり16m前後であることが確認できました。

※生データや他アトラクション(スペースマウンテン・ビッグサンダーマウンテン)の比較については、別記事で公開中です。
動画でも確認してみよう
もしスプラッシュマウンテンに乗ったことがない方は、下の動画で7分頃からの様子をチェックしてみてください。映像で見ると「それほどでも…?」と思うかもしれませんが、実際に乗ると迫力が違います!
じゃあ、計算してみよう!物理の出番です
さて、ここからが理科の本領発揮です。スプラッシュマウンテンにはエンジンがついているわけではなく、最高点から重力の力だけで一気に落ちていきます。このような場合、エネルギー保存の法則を使って「落差から速度を予測する」ことができます。
■ 使用する物理公式
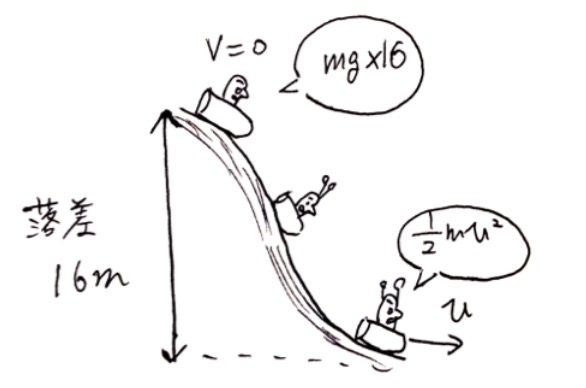
位置エネルギー(mgh)=運動エネルギー(½mv²)
→ よって
\[v = \sqrt{2gh}\]
ここで、
g = 9.8 m/s²(重力加速度)
h = 16 m(高さ)
計算すると、
\[v = \sqrt{2 \times 9.8 \times 16} \approx \sqrt{313.6} \approx 17.7 \, \text{m/s}\]
→ km/hに直すと
\[17.7 \times 3.6 \approx 63.7 \, \text{km/h}\]
✅ 結果:約64km/h!
なんと、公式データの「最高速度62km/h」とほぼ一致しているのです。
物理の計算、スゴい。
授業で使うならここがポイント!
• 実際に乗った経験のある生徒が多いので、導入が非常にスムーズ
• エネルギー保存の法則の応用例として最適
• 「感覚と理論の一致」を体験でき、学習意欲アップにつながる
同様に、富士急ハイランドにあるFUJIYAMAも同じ方法で求めることができます。
FUJIYAMAの公式HPを見ると、最大落差70m、最高速度130km/hと記載されています。
それでは力学的エネルギーの保存則をつかって計算をしてみよう。先程のhの部分に70を入れて計算すると、
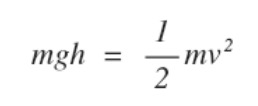
v=√(2×9.8×70)
v=37m/s、時速にすると、133.2km/hとなり近い値となりますね。面白い!でも、なぜかスプラッシュマウンテンもFUJIYAMAも理論値より、実際の最高速度はわずかに小さな数字になっています。なぜでしょうか。
外力がはたらいているけれど…
このようにジェットコースターまたは振り子などでは「力学的エネルギー(運動+位置+弾性エネルギー)」は、ほぼほぼ保存します。でもちょっと考えてみてください。ジェットコースター(または振り子)には垂直効力(または張力)などの「外力」がはたらいています。外力がはたらくと力学的エネルギーは保存しないはずです。
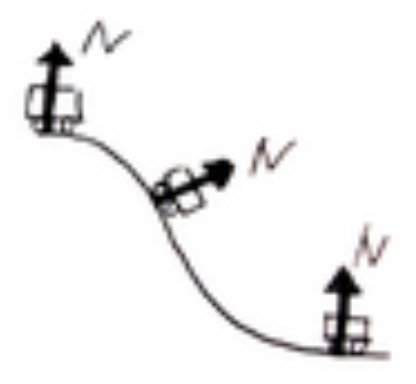
これはいったいどういうことなのでしょうか?実は、垂直効力や張力が常に物体の運動方向と垂直にはたらいているからです。運動方向に対して垂直な力のする仕事は0なので、力学的エネルギーのみを考えてよいのです。
ジェットコースターの場合
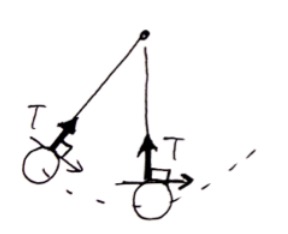
振り子の場合
垂直効力や張力は実際にその大きさを求めるのが大変ですが、このように仕事をしません。よってどのような経路をたどったとしても力学的エネルギーは保存をするのです(では垂直抗力や張力はこの運動にとってどのような影響を及ぼしているのでしょうか?)
これらのことから、アルプスの少女ハイジの乗っているブランコのスピードを求めたりすることができます。オープニングのはじめにでてくる大きなブランコのことです。
例えばですが、ブランコのヒモの長さが30m(ブランコの周期からだいたいの長さがわかります)、角度が60°とすると、最下点での速度はどうなるのでしょうか。ハイジはニコニコわらっていますが、結構な絶叫マシーンだということがわかります。
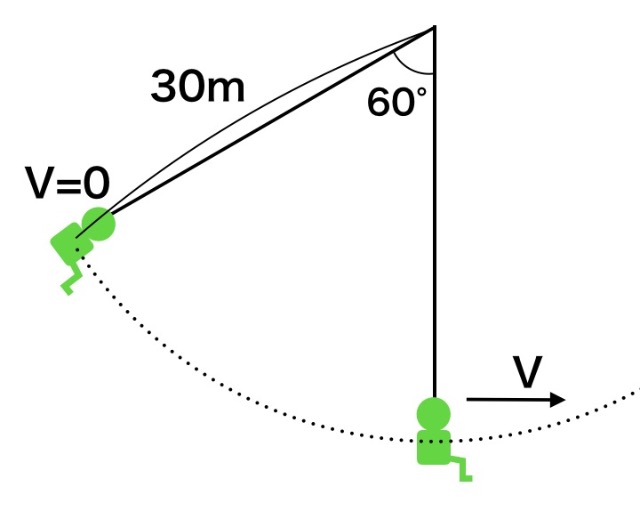
ぜひ自分で計算をしてみましょう。
まとめ
身近な遊園地のアトラクションが、実は教科書の知識で解き明かせる――そんな「日常と科学のつながり」を実感できるのが、この授業の一番の価値です。学びは教室の中だけじゃない。遊園地も、教材になるんです。
オンライン授業はこちらからどうぞ
#力学的エネルギーの保存 #力学的エネルギー #仕事 #ディズニーランド物理学

|
力学的エネルギーの保存を用いて、ジェットコースターの速度を計算してみましょう! |

|
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・運営者・桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20

テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日放送予定「チコちゃんに叱られる」(NHK)の科学監修しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。



