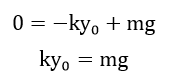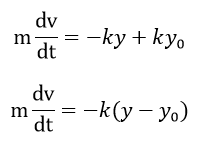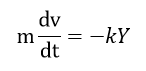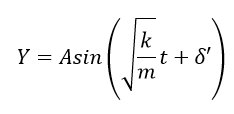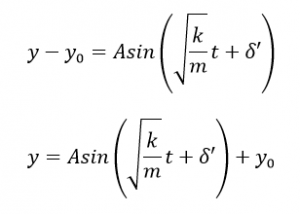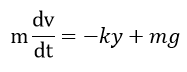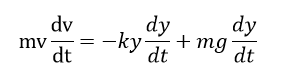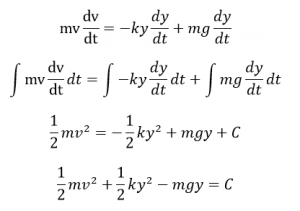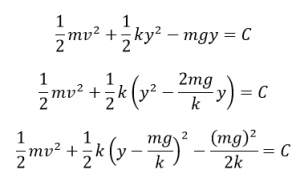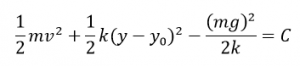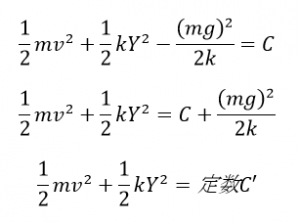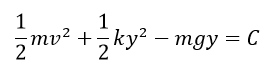単振動を深掘り！つり合いの位置が鍵だった？微積で整理する物理

サイエンストレーナーの桑子研です。毎日が実験。

微積でわかる単振動の世界〜鉛直ばね振り子の謎を解く〜

高校の物理では、「微分積分」を使わずに教科書が書かれていることがほとんどです。これは、多くの高校で物理の授業が数学Ⅲよりも先に進むからですが、「微積を使ったほうが物理の本質がスッと理解できる」という場面がいくつもあります。

たとえば、運動方程式の導出、エネルギーの保存則、そして今回のテーマであるばねによる単振動などです。

高校物理では微積を扱うことはありませんが、先生方が内容理解を深めたり、授業中の補足説明に活かすことは大いにあります。「この現象は実は高校以降ではこんなふうに式で表すことができるんですよ」と伝えるだけで、生徒の目の輝きが変わる瞬間もあるはずです。

このシリーズでは、微積で解くと見通しがよくなる高校物理の単元を、一つずつかみ砕いて紹介していきます。今回は鉛直ばね振り子の単振動と力学的エネルギー保存について、微積を使ってスッキリと解き明かしてみましょう。

鉛直ばね振り子の運動を見てみよう

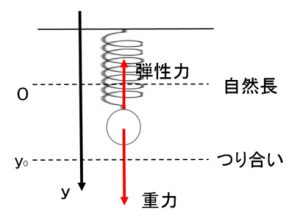
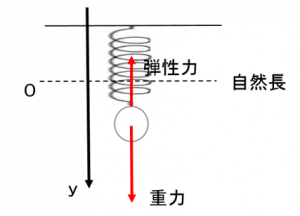
まずは定番、天井からばねをつり下げて、その先におもりをつけた鉛直ばね振り子を考えます。

このとき物体にはたらく力は以下の2つ：
• 下向きの重力 mg
• 上向きのばねの弾性力 -k y（ばね定数 k、伸びを y とする）

運動方程式は、下向きを正とするとこう書けます。

\[m\frac{d^2y}{dt^2} = mg – ky\]

この式、右辺に定数項 mg が含まれているため、単振動の典型的な形

－定数×変位の形になっていないため、単振動をするかどうかはわかりません。

またおもりのつりあいの場所におけるばねの長さをy₀と置くと、力のつりあいから次のようにして、求めることができます。

この式を邪魔であった上の式のｍｇのところに代入してみましょう。

となりました。ここでy－y₀をYとすれば、

となり、－定数×変位の形になりましたので、この運動も単振動をするということになります。

ちなみにYが０のときが振動の中心になるので、そのときにｙの値はy－y₀＝０なので、y=y₀です。ということで、次の図のように自然の位置を中心とした単振動をするということになります。

ここで、Yをｙで表せば、

となることからも、単純にy₀の分だけ、振動の位置がずれているということがわかりますね。

このようなことから、鉛直ばね振り子等の定数がついた場合については、釣り合いの位置での単振動と考えてとくことができるのですね。

力学的エネルギー保存の見方が変わる！

さらに面白いのはエネルギー保存則の表現です。運動方程式を積分することで、力学的エネルギーについて見て行きたいと思います。両辺にv=dy/dtをかけます。

時間で積分します。

運動エネルギー＋弾性エネルギー－位置エネルギー＝定数

※　Cは積分定数

となります。これは力学的エネルギーの保存を示します。位置エネルギーが負になっているのは、今回の単振動の原点を自然長でとっているためです。

このように一般的にといていくと、力学的エネルギーの保存の中には、位置エネルギーの項が入ってくるので、しっかりと位置エネルギーを考えなければいけません。

しかし、今回の運動は「つり合いの位置」を基準とした単振動をすることがわかりましたよね。単振動は、運動エネルギーと弾性エネルギーの２つのエネルギーのやりとりなので、位置エネルギーは考える必要はありないはずです。というわけでつり合いの位置をうまく使って、上の式を書きなおしてみましょう。

つり合いの位置は、ky₀=mgだったので、

y－y₀=Yとおいたことから、

運動エネルギー＋弾性エネルギーのようなもの＝一定

というようになります。Yはつり合いの位置を原点としたときの長さを表しますので、つり合いの位置を基準とすれば、この式をつかってもよいということになります。

「弾性エネルギーのようなもの」という表記にしましたが、この1/2kY^2という項は実はこの中に位置エネルギーが含まれているので、「のようなもの」という表現にしました。ここに注意をしましょう。

間違えやすいところなので、比較をしておくと、

＜原点が自然長とした場合＞

運動エネルギー＋弾性エネルギー＋－位置エネルギー＝一定

＜原点をつり合いの位置とすると特別な式になる＞

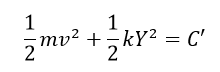
運動エネルギー＋弾性エネルギーのようなもの＝一定

となります。気をつけておきましょうね。

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！

２月のイチオシ実験！梱包材で遊ぼう！

• 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう！→ やめられなくなる！静電気実験２０

体中に梱包材をはりつけてみよう！

テレビ番組等・科学監修等のお知らせ

• 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。

書籍のお知らせ

• 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
• サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師等・ショー・その他お知らせ

• 2/20（金）「生徒の進学希望実現支援事業」研究授業＠福井県立若狭高等学校　講師
• 3/20（金）　日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③　11:20-12:20
• 7/18（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
• 10/10（土）　サイエンスショー予定
• 各種SNS　X(Twitter)／instagram／Facebook／BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。