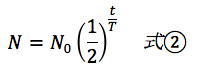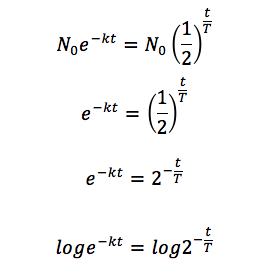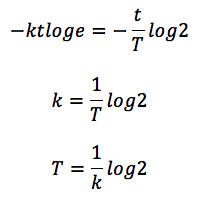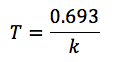その公式、どこから来たの？微積で解き明かす放射性崩壊のヒミツ（高校物理と微積分）
サイエンストレーナーの桑子研です。毎日が実験。
微積で見る高校物理 〜放射性崩壊と半減期の“スッキリ”した関係〜
高校物理では、基本的に微分積分を使わずに現象を説明しています。これはもちろん、数学の進度との兼ね合いがあるためです。微積が未習の段階でも理解できるように、物理ではグラフや比例関係、経験則に基づく数式などを使って表現されています。
しかし、微積の道具を使うと、物理の見通しがグッと良くなる場面もたくさんあります。物理が“ただの公式暗記”になってしまう原因の一つは、「なぜその式になるのか」が見えにくいことにあるかもしれません。微積を使うと、物理の背後にある変化の仕組みが明快に立ち上がってくるのです。
今回はその一例として、「放射性崩壊」と「半減期」の関係を、微積の視点から見ていきます。
放射性崩壊と微分方程式
放射性崩壊の基本的な考え方は、「原子核の数は時間に応じて減っていく」というものです。これを数学的に表現すると、
dN/dt = -kN
（kは崩壊定数）
この方程式を解くと、次のような指数関数の形になります：
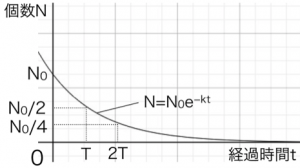
N(t) = N₀ × e^(−kt)
ある時刻の数N＝はじめの数N0×ネイピア数e^（−崩壊定数k×ある時間ｔ）
この式は、ある時刻tにおける放射性原子の数Nを、初期の数N₀と崩壊定数kから求めることができるというものです。
高校物理で登場する“半減期”との関係
ところがこの式、高校物理の教科書には出てきません。高校では、「半減期T」という時間の単位を使って次のように表現されます。
半減期Tごとに、原子核の数は半分になる
指数関数eと、1/2の累乗の形。この2つの式は同じものを表しています。ではどうやってつながっているのでしょうか？なお半減期Tとは、元の数の半分になるまでの時間で、例えば半減期の時間がたつと、どんどん1/2倍になっていきます。
よって上の式のようになります。式①のｋ（崩壊定数）を使った式で表現するよりも、半減期を使ったほうがわかりやすい、イメージしやすいため、この半減期Tはよく使われています。
2つの式の橋渡し：kとTの関係
先ほどの微積で導いた式と、半減期の式を見比べてみましょう。
微積バージョン：
N = N₀ × e^(−kt)
半減期バージョン：
N = N₀ × (1/2)^(t/T)
同じNを表しているのだから、右辺が一致するはずです。
つまり、
※ ここでlogの底はe
log2=0.693より、
理科教師として知っておきたいこと
高校物理では、この半減期の式を知っていれば問題を解くことはできるのですが、半減期ぴったりではない時間を問われた場合には、どうしても対数の知識が必要になってきます。
また「崩壊定数k」と「半減期T」がまったく別の表現方法でありながら、同じ現象を描いていることが明確にわかります。中学校理科の中では、微積分を使うことはありませんが、「指数関数的に減る」「半分になる時間が一定」といった現象のイメージは、生徒の段階でも伝えることができます。
おわりに
高校物理を微積の視点で見直すと、バラバラだった公式が“一本の筋”でつながっていることに気づきます。放射性崩壊と半減期の関係はその代表例。
今後も、理科の先生向けに、微積と高校物理を結ぶ「なるほど！」な内容をシリーズでお届けしていきます。ご関心あれば、続編もお楽しみに！
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
７月のイチオシ実験！
夏でプシュッと爽やか実験！
テレビ番組監修・イベント等のお知らせ
- 6月30日（火） 6/30 23:56〜 【科学監修・出演】「地球まるごと大実験ネイチャーティーチャー」（TBS）
- 7月18日（土） 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 12月26日（土） ナリカサイエンスアカデミー（教員向け実験講習会）開催
書籍のお知らせ
- ７月16日発売 『高校入試 分解問題集 理科』（学研）…難しい問題も小さな問題に分解することで、問題を解くことができます。そんな分解の技術が身につくように深く関わりを持って作りました。
- 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
- 『きめる!共通テスト 物理基礎 改訂版』（学研）… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。
各種SNS（更新情報をお届け！）
【日本語】X(Twitter)／instagram／Facebook 【英語】BlueSky／Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
- 6/30（火）23:56〜 ランボルギーニでテーブルクロス引き！？TBSで監修実験がふたたび放送されます（地球まるごと大実験ネイチャーティーチャー）
- 水を注いだら立方体が現れた！ 光と色の「引き算」が生み出す CMYウォーターキューブ（ナリカ）
- 【サイエンスショー講師】こまもブーメランも宇宙も同じ！「回転の科学」で小学生が大興奮した2時間（ダヴィンチマスターズ）
- 発泡スチロールが宙に浮く「音の正体」を目で見せてくれる不思議な装置（クント管）
- スイッチを切っても止まらない！コイルが見せる電気振動の正体をセンサーで捉えた（EasySense V-Hub）
- 【公開研究会】脱作業化！デジタル化と段階的指導で実現する オームの法則の探究
- パンチの数とダメージは別もの！ベクレルとシーベルトをボクシングで理解する
- 渦電流で大ジャンプ！電磁誘導の奇跡―金属の輪が宙に浮く理由（つくばエキスポセンター）
- ピンポン球286個でニホニウムを作ったら、箱からはみ出すレベルだった
