「変位」がわかれば物理が解ける！鉛直投げ上げの数式に隠された本当の意味

サイエンストレーナーの桑子研です。毎日が実験。

空に向かってボールを投げ上げたとき、そのボールは最高点まで昇り、一瞬止まったかのように見えてから再び地面へと落ちてきます。この一連のドラマチックな動きを、理科の授業では「ひとつの数式」だけで説明してしまいます。でも、ちょっと不思議に思いませんか？「上っているとき」と「落ちているとき」では、動いている向きが全く逆です。それなのに、なぜ途中で式を変えたり、座標軸を引き直したりしなくていいのでしょうか。

今回は、物理を初めて学ぶ多くの高校生が一度は抱くこの疑問を、科学の視点でスッキリ解決していきましょう！なおわかりやすさを優先しているための記事であること、ご了承ください。初学者の多くは文字式の扱いに困難さを覚えるため、あえて文字の中に具体的な数字を入れるなどをしています。

なぜｙ軸をとりなおさなくていいの？

放物運動の中には、「鉛直投げ上げ運動」というものがあります。これは初速度を上向きに与える運動で、一般的には上向きにy軸をとり、地面を高さ0mとして設定します。そして、位置の式や速度の式を使って、物体の未来の位置を予測するのです。

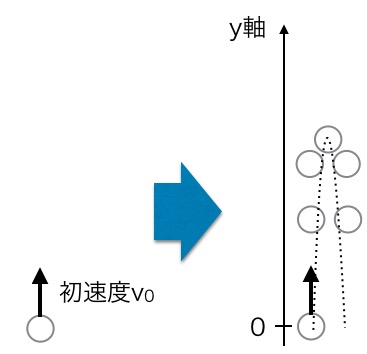
＜鉛直投げ上げ運動＞

位置の式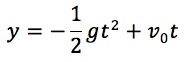

速度の式

ここで、真面目に考える生徒さんほど、こんな疑問を持ってくれます。 「最高点に物体が達したときに、y軸をもう一度設定し直して、自由落下の式を考えなくてもいいのですか？」

最高点に達したときに、もう一度軸を設定し直したくなる。

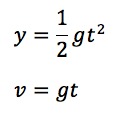
使う数式は最高点ではボールは静止しているから、自由落下！

実はこれ、数学が得意な生徒さんほど陥りやすいポイントでもあります。「頂点からは別の動きになるはずだ」という直感が働くのですね。

結論から言うと、軸を設定し直して計算しても答えは出せます。間違いではありません。しかし、実はその作業は「無駄」なのです。なぜ書き直す必要がないのか、その理由を見ていきましょう。

「別の運動」に見えるワナ

y軸を書き直すべきだと感じてしまう理由は、私たちの感覚が次のように判断するからです。

最高点以降は、物体が折り返して落ちてくる。

y軸（上向き）に対して、進む方向が逆になった。

つまり、さっきまでの運動とはルールが変わったはずだ！

しかし、物理の世界では、物体にかかっている「重力」に注目します。上っているときも、最高点にいるときも、落ちているときも、物体には常に「下向きの重力」が一定にかかり続けています。ルール（加速度）はずっと変わっていないのです。

具体的な数字を使って検討してみよう！

「理屈はわかったけれど、やっぱり不安……」という時は、具体的な数字を入れて確かめるのが一番です。これは科学者が新しい理論を検証するときにも使う、非常に強力な方法です。

例えば、重力加速度gを10、初速度v0を20としてみましょう。

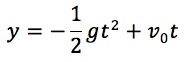
ここに代入

この式に、時間を0秒から4秒まで順番に代入してみます。

・0秒：0m

・1秒後：-5 + 20 = 15m

・2秒後：-20 + 40 = 20m（ここが最高点！）

・3秒後：-45 + 60 = 15m

・4秒後：-80 + 80 = 0m（地面に戻った！）

値をグラフにしてみると、どうでしょうか。

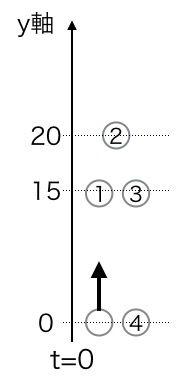
見事に、物体が昇ってから同じ道を通って落下してくる様子が再現できています。そう、同じ式がそのまま使えるのです。

「変位」と「移動距離」の違いがカギ！

なぜ同じ式で大丈夫なのか。その秘密は「y」という文字が何を表しているかにあります。ここで大切なのが、「変位」と「移動距離」の違いです。

物理の式におけるyは「変位」、つまり「最初の位置から見て今どこにいるか」という位置の情報を指します。

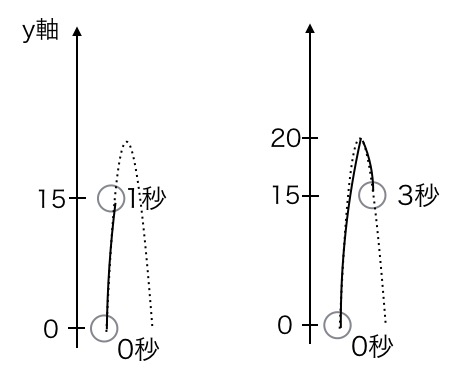
左の図（上昇中）は、移動距離も変位も同じ15mです。 しかし右の図（落下中）を見てください。移動距離は「行って（20m）戻った（5m）」ので合計25mですが、変位（地面からの高さ）は15mです。

投げ上げの式にあるyは、あくまで「地面からの高さ（変位）」を教えてくれるもの。だから、途中で道を引き返していても、何の問題もなく正しい高さをはじき出してくれるのです。

数式が描く「放物線」の美しさ

数学的に考えてみると、さらに納得がいきます。位置の式yは、時間tの2次関数になっています。

t = 2のときにyは最大値20に達する

グラフに描くと、綺麗な左右対称のカーブになります。

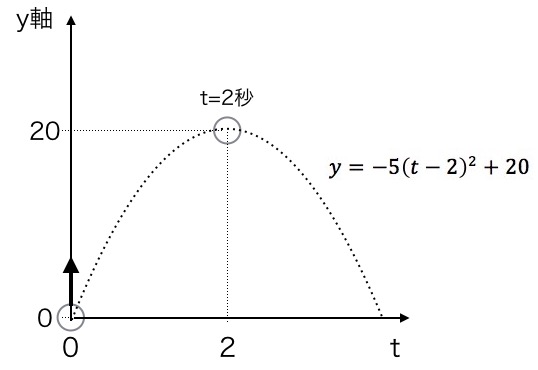
2次関数のグラフが「放物線」と呼ばれる理由がここにあります。投げ上げられたボールの軌跡そのものが、数式の中に美しく組み込まれているのですね。

速度の「マイナス」が教えてくれること

速度の式についても確認しておきましょう。

数字を代入するとこうなります。

・0秒：20m/s

・2秒：0m/s（一瞬静止）

・4秒：-20m/s

この「マイナス」こそが、物理の面白いところです。物理における「速度」は向きの情報を持っています。プラスが「上向き」なら、マイナスは「下向き」を意味します。

一方で、日常で使う「速さ」は動きの激しさ（大きさ）だけを指します。0秒のときも4秒のときも、速さは同じ20m/s。でも速度は＋20と−20で「別物」として区別されます。このおかげで、ひとつの式で逆方向の動きまで表現できるのです。

まとめ：ひとつの数式を信じて進もう

鉛直投げ上げの式は、物体が最高点を過ぎて落ちてくるときまで、ずっとあなたに正しい位置と速度を教えてくれます。「式はひとつで大丈夫」。そう信じて安心して計算に使ってください。

もちろん、最高点から「自由落下」として解き直す発想も、物理の仕組みをよく理解している証拠で素晴らしいものです。でも、こうして数式の裏側にある「変位」や「速度」のルールを知ると、物理がもっとシンプルでエレガントなものに見えてきませんか？

迷ったときは具体的な数字を入れてみる。この科学的な姿勢を、ぜひこれからも大切にしてくださいね。

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！