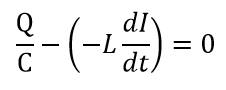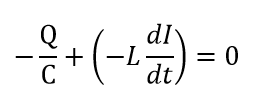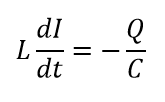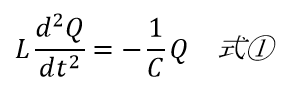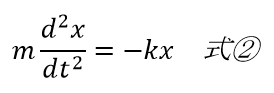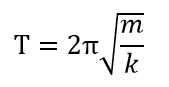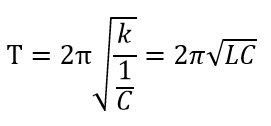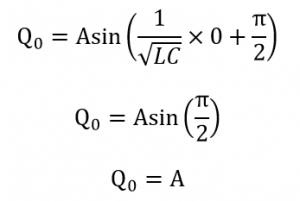微積で見るブランコの振動と電気振動【リモート授業】

サイエンストレーナーの桑子研です。このサイトで科学を一緒に楽しみましょう。 

 

位置エネルギーから

運動エネルギー

高校物理と微分積分

高校物理の教科書では微積を使わないで説明がなされています。数学の進度の関係もあるため、そのようになっていますが微積をつかって考えたほうがスッキリとわかりやすく説明できることも数多くあります。

このコーナーでは微積を使ったほうが良い範囲について、ひとつひとつ説明をしていこうと思います。今回は電気振動についてみていきましょう。

電気振動と微積分

充電したコンデンサーとコイルを接続すると、コンデンサーとコイルの間で電荷が行ったり来たりする電気振動という現象が起こります。この振動は力学の単振動と同じように表すことができ、コンデンサーに電荷が最大にたまった時と、コイルに流れる電流が最大になった時のエネルギーの保存から、高校物理では解かせるような問題がでます。電気振動の周期は次の式で表されました。

　高校物理の教科書では、このようになりますよ。というようにしか書かれていないのですが、今回はこの振動現象について、単振動の様子と比較をして、微積分を使って考えていきたいと思います。

 電気振動とキルヒホッフ第二法則

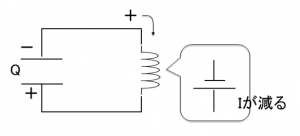
あるときにコンデンサーにたまった電荷をQとして、この電荷がコイルに流れ込んで、コイルに流れ込んでいく電流Iが増えていくことを考えます。

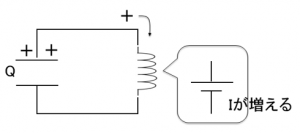
回路に流れる電流の向きを時計回りの回転を正と決めると、キルヒホッフの第二法則から

となります。

またコンデンサーにたまった電荷がすべて放出されて、極板の電荷が０になっても、コイルの自己誘導という性質によって、コンデンサーの極板からはさらに電荷が運ばれていきます。

このような状態になったときのキルヒホッフの第二法則を考えて見ると、

となります（反時計回りに流れる電流の方向を正としました）。２つの式を比べると、同じ式になっているのがわかりますね。

このことから、この式を定数と変数でわけて、単振動のような式へと展開することができます。

I＝ｄQ／ｄｔより、

定数×Qの２回微分＝－定数×Q

　この式とばねの単振動のときの運動方程式を比較してみましょう。

定数×ｘの２回微分＝－定数×ｘ

　まったく同じような形になっているのがわかりますね。よってこの場合は電荷が行ったり来たりと単振動と同じように振動をすることがわかります。この方程式は、単振動と同じように解くことができるはずなので、一般解は

 

　となるはずです。これを時間微分することによって電流が求められます。

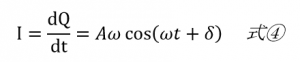
このようにコンデンサーにたまる電荷が振動をしているので、当たり前ですが、電流も振動していることがわかります。

また微分方程式の電気振動の式①と、ばねの振動の式②の対応関係から、ｍ=L、ｋ＝1/Cとなることがわかります。単振動のバネの周期の公式は、

となっていたので、この電気振動の周期を示す式は、

となり、電気振動の周期の公式になりました。なおこの周期の式から電気振動の角周波数ωは、ω＝２π/Tより、ω=1/√LCとなります。

振幅Aについては、コンデンサーにたまっている電荷の最大値をQ₀とすると、この電荷は時刻０のときに電荷Q_０たまっている状態でスタートしたとすると、上の式③の初期位相δはπ/2となります。

これらのことから振幅AはQ₀となります。

また時刻０のときの電流Iはまだ０になっているはずですが、式④にさきほどの初期値を代入してみると

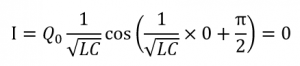
となり、たしかにまだ回路には電流が流れていないことがわかります。これらの初期条件をつかって数式をもう一度書き直すと、式３となり、I=dQ/dtなので、式４のようになります。

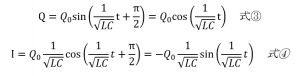
Qはcosで、Iはsinなので、このことからコンデンサーにたまる電気量と、コイルに流れる電流Iが位相πずれて振動をしていることが示されました。

エネルギーの保存について

微分方程式の電気振動の式①と、ばねの振動の式②の対応関係から、ｍ=L、ｋ＝1/Cとなり、またv=dx/dt、I=dQ/dtの対応関係から、v=I、x=Qの関係がある。

よって力学的エネルギーの保存と同様に電気振動のエネルギー保存式も作ることができる。

　またコイルに流れる電流が最大になったとき、コンデンサーに電荷がたまっていないので、エネルギー保存則から次の式がたてられます。

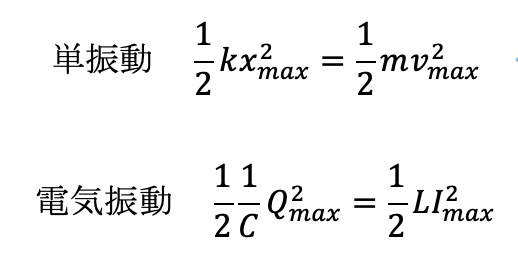
　教科書によってはこのように電圧の最大値で書かれている場合もあります。

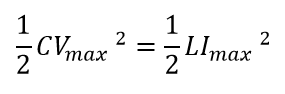
微積で考えると、途中の様子まで描けるところが面白いですよね(^^)

ニュースレター

・ニュースレターはブログでは載せられない情報を配信しています。

[subscribe2]

@kuwakoさんをフォロー

２月のイチオシ実験！梱包材で遊ぼう！

• 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう！→ やめられなくなる！静電気実験２０

体中に梱包材をはりつけてみよう！

テレビ番組等・科学監修等のお知らせ

• 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。

書籍のお知らせ

• 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
• サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師等・ショー・その他お知らせ

• 2/20（金）「生徒の進学希望実現支援事業」研究授業＠福井県立若狭高等学校　講師
• 3/20（金）　日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③　11:20-12:20
• 7/18（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
• 10/10（土）　サイエンスショー予定
• 各種SNS　X(Twitter)／instagram／Facebook／BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。