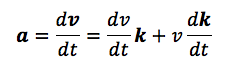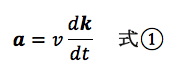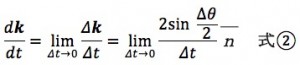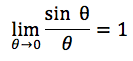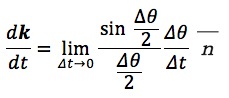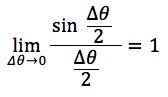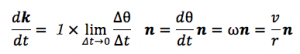微積でスッキリ！円運動の加速度を数学的に導いてみよう（微積分その４）
高校の物理では、数学の進度の関係もあり、微積分を使わずに説明されることが一般的です。しかし、実際には微積分を用いることで、物理の概念をよりスッキリと理解できることが多くあります。
例えば、運動の公式やエネルギーの関係式など、微積を使えば「なぜこの式になるのか？」という疑問がクリアになります。ただ暗記するのではなく、理論的な背景を理解できるのが微積の強みです。
今回は、微積を使ったほうが理解しやすい範囲の解説シリーズ第4回として、「円運動の加速度」の導出を行ってみましょう！
円運動とは、物体が一定の半径を持つ円軌道を描きながら運動する現象です。このとき、物体には「向心加速度」と呼ばれる加速度が生じます。この向心加速度を、微積を使ってどのように導出できるのか、一緒に考えていきましょう！
前回の記事はこちらをご覧ください。
円運動の加速度の大きさは、
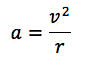
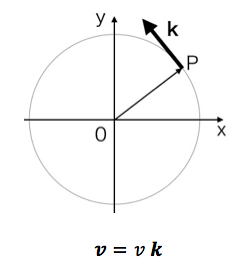
と表されますね。向きは円の中心方向を向きます。このことについて考えてみましょう。次の図のように円上を等速で動く、ある点Pの速度vは、点Pでの接線方向を示す単位ベクトルkを使って、
（速度＝速さ×接線方向の単位ベクトルｋ）
と表されます。ここで太字はベクトル量を示します。
加速度の定義から、速度を微分してみましょう。
となります。ここで右辺の１項は速さの変化（dv/dt）を示しています。等速円運動の場合には、速さの変化がないので、この項はdv/dt=0より、０になります（等速ではない場合には、必要になります）。２項は単位ベクトルｋの変化による加速度を示します。つまり速度の向きの変化によって必要な加速度です。
今回は等速円運動の場合について考えるので、１項は０にして２項にのみ焦点を絞ります。
それでは、このdk/dtについて求めていきましょう。
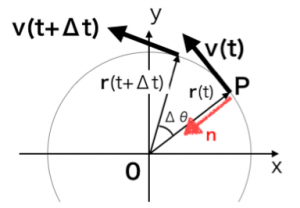
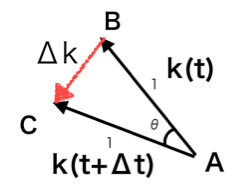
ｄｋを求めるために、２つのベクトルの始点をそろえて、Δｋについて考えてみましょう。ここでnバーについては、三角形BCの方向を持つ単位ベクトルとしました。単位ベクトルｋの変化量であるΔｋは、２つの速度の単位ベクトルk(t)とk(t+Δt)を並べて見ると、次の場所になります。
このことからdk/dtについては次のように表すことができます。
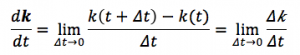
二等辺三角形ABCの角Aから二等分をすると、直角三角形２つにわけられます。
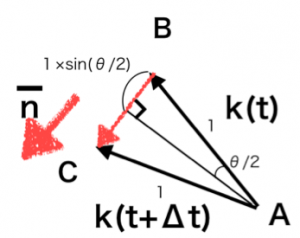
このためΔkの値の大きさは、１×sin(Δθ/2)×２となります。BCの向きを向いた単位ベクトルｎバーを使うと、
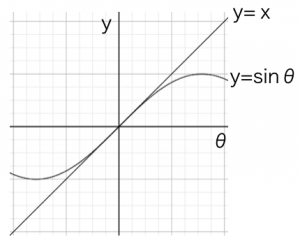
となります。Δｔを０に近づけると、Δθは０に近づき、かつ角ABCは９０°になるため、nバーは、ABの接線である単位ベクトルｎになります。また別の数学の公式として、
という関係式があります。これも使います。
それでは、これらのことから、式②のdk/dtを作り替えていきます。
ここで、Δｔ→０のときΔθ→０なので、
となり、またΔｔ→０のとき、ｎバーは単位ベクトルｎになるので、
となります。このことから、加速度は次のようになります。
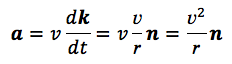
公式を導くことができました。
高校物理の教科書を開くと、このようなことについて微積を使わないで説明がされています。ただし少し違和感を覚えるところがあるかもしれませんね。それは、今回のような微積を使わないで、頑張って説明をしているからそう感じるのかもしれません（＾＾；）。
参考としたのは、新物理入門と数学の本です。新物理入門は理系に進む人は必読書です。少しむずかしいですが、ぜひ受験中または、終わった時に手をだしてみてくださいね。
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・運営者・桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！
科学のネタチャンネルでは実験動画を配信中！
