三角関数が苦手ではありませんか？

物理基礎のテストをみていると、三角関数が出てくると突然できなくなる生徒もいるようです。

ぼく自身、はじめてサインやコサインに出会った時は、

「なんじゃこりゃ〜〜」

と思って、なんとなく苦手意識をもちました（＾＾；）

でも三角関数はとりあえずの慣れなんですね。
慣れてしまえば、どうってことはない。
単なる数字の一つなのです。

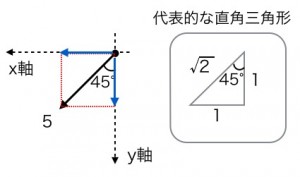
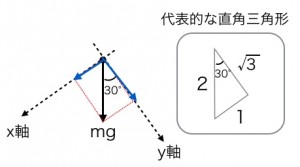
また覚える必要もとくにはなく、最終手段としては代表的な直角三角形の比さえ

覚えていればいいだけです。

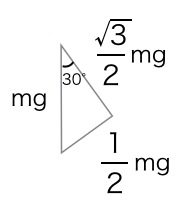
ちなみに代表的な直角三角形とは１：２：√３である３０°の直角三角形、
１：１：√２である４５°の直角三角形だけです。

物理基礎ではこの２つの直角三角形以外は、ほぼでてきません。

それでは、はじめに三角関数を使った解き方と、
三角関数を使わないで解く方法について、見て行きましょう。

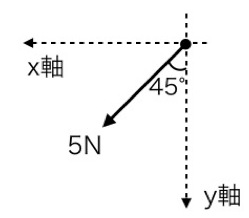
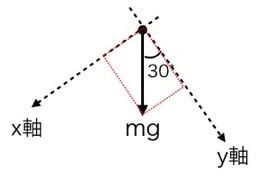
例えば次のような問題があったとします。
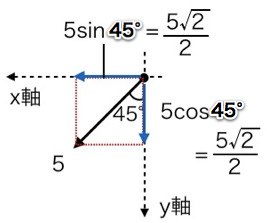
簡単な力の分解ですが、ベクトルが苦手な人も多いと思います。

次の力をそれぞれｘ軸とｙ軸に分解したとき,それぞれの方向の力の大きさを作図して求めなさい。なおx軸とy軸は直交しています。

(1)

(2)

解答・解説）

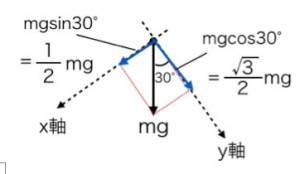
(1)　ベクトルの分解の３ステップをつかって、力を分解していきましょう。

３ステップ解放

①　x軸・それに直交するようにｙ軸を作る。
②　矢印が長方形の対角線となるように、長方形をつくる。
③　２本の矢印に分解する。

それではやってみましょう。ステップ①の軸の作図については、もう済んでいるため②からはじめます。
②　矢印が長方形の対角線となるように、長方形をつくる。

③　２本の矢印に分解する。

　θのついた矢印はcosを使うのでしたね。またついていない方の矢印はsinを使います。

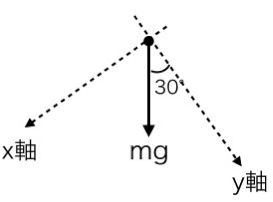
(2)　(1)と同様に、ベクトルの分解の３ステップをつかって、力を分解していきましょう。

②　矢印が長方形の対角線となるように、長方形をつくる。

　今回はx軸、y軸に従うため長方形が斜めになります。斜面上の運動を扱うときに、このような分解をよく行います。

③　２本の矢印に分解する。

別解

三角関数のsinやcosが苦手な人も多いかもしれません。

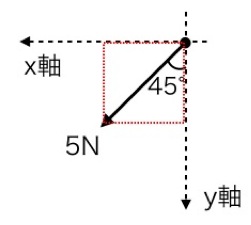
もし苦手であれば、代表的な直角三角形のそれぞれの辺の比さえおぼえておけば、三角関数を使う必要はありません。

例）
(1)の問題の場合

(2)の問題の場合

いかがでしたか？苦手意識を持つこともありますが、最終手段は比さえおぼえておけばいいということで、はじめの苦手意識を克服してほしいと思います。

慣れてくれば、三角関数なんてなにも怖くなりますよ。

＜物理基礎の参考書をかきました＞

きめる!センター物理基礎【新課程対…
桑子研

次の科学のタネ

質問を募集しています。

・科学のネタから出た本はこちらです。

・ニュースレターはブログでは載せられない情報を配信しています。ぜひご登録ください！ニュースレターはブログでは載せられない情報を配信しています。

[subscribe2]

@kuwakoさんをフォロー

・動画授業をはじめました。