先生も一緒に悩みたい。生徒の探究心を爆発させる「同伴者」としての授業づくり（フックの法則）

サイエンストレーナーの桑子研です。毎日が実験。

突然ですが、みなさんは「ばね」を伸ばしたことがありますか？ぐいーんと伸びるあの感触、なんだか面白いですよね。今回は、中学1年生の理科の授業で行った「フックの法則」の実験についてお話しします。ただ教科書通りに教えるのではなく、生徒たちがまるで科学者のように悩み、発見するプロセスを大切にした授業実践です。教室で起きた小さなドラマを、少し覗いてみてください。

教科書にはない「余白」をつくる

中学1年生にとって、フックの法則の実験は初めて行う「本格的な定量実験」になります。定量実験とは、数値を使って物の性質を調べる実験のことです。通常、学校の実験といえば「おもりは〇個使って、〇cmごとに記録しなさい」と、料理のレシピのように手順が決められていることが多いものです。でも、今回はあえてそれをしませんでした。「ばねののびと力の関係を知りたいけれど、どうやって調べたらいいと思う？」と問いかけ、実験計画そのものを生徒たちに委ねたのです。

おもりは何個必要なのか？ 測定する間隔はどうするか？

これを自分たちで決めるのは、実はとても勇気がいることです。しかし、この「自分たちで条件を決める」というプロセスこそが、科学的な思考の第一歩です。「なぜその設定にしたのか」という根拠を考えることで、やらされる実験から、自分たちの実験へと変わっていくのです。

実験データは「物語」の始まり

まずは仮説です。仮説というよりも予想に近いでしょうか。意外に真っ直ぐではないという意見も多くありました。

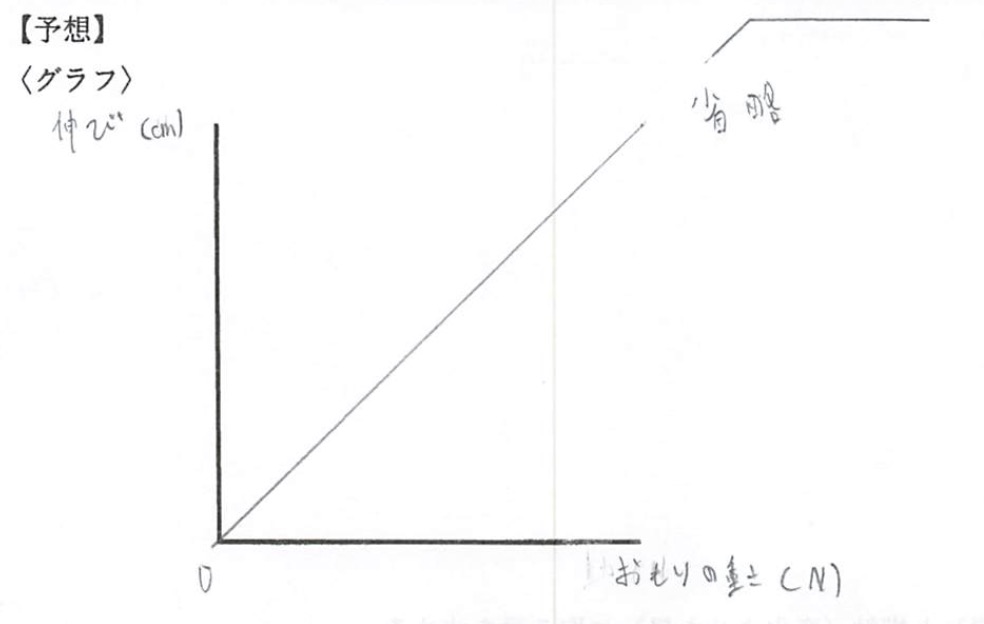
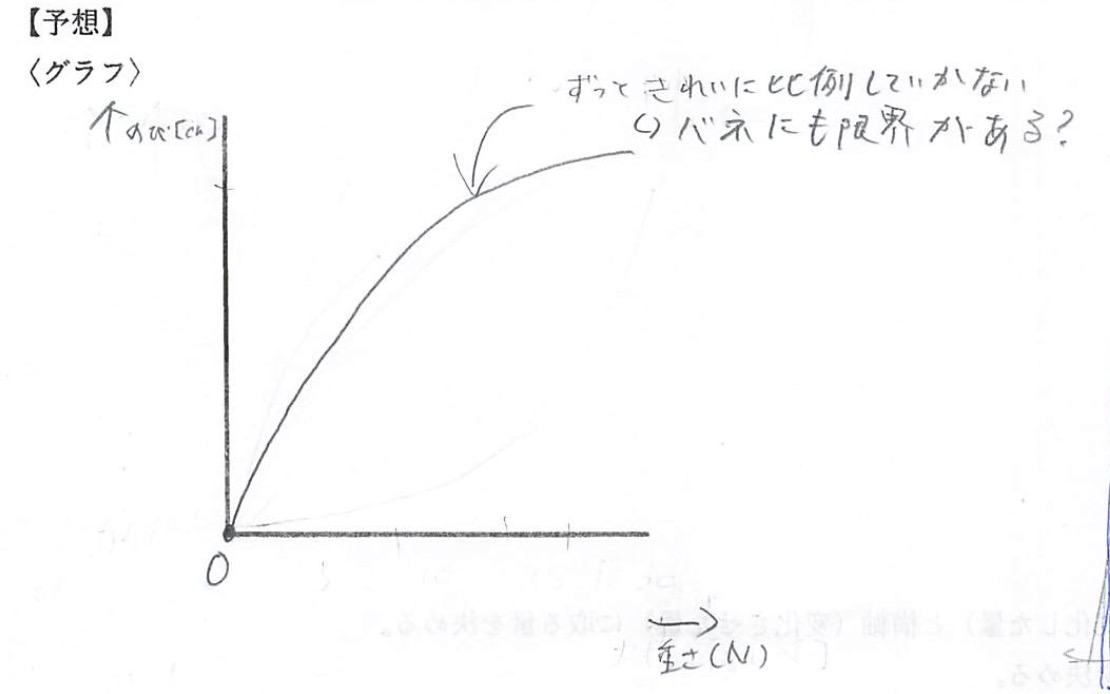
自分たちで立てた計画に従って、いよいよ実験スタートです。色々な幅で実験をする生徒が出てきました。

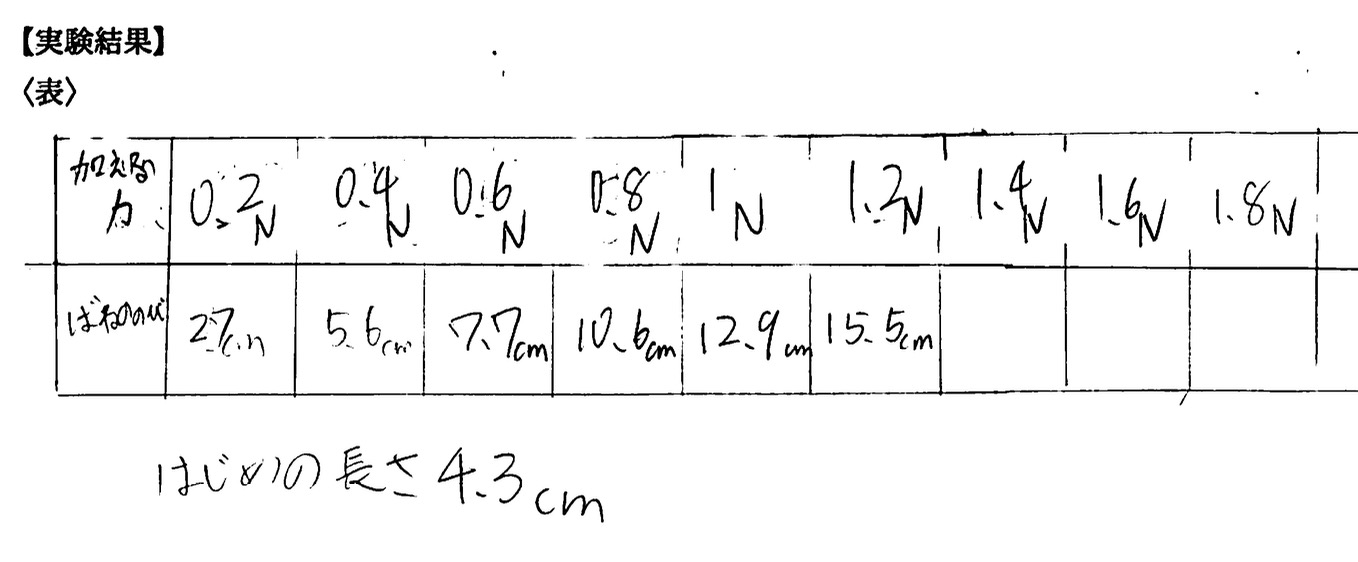
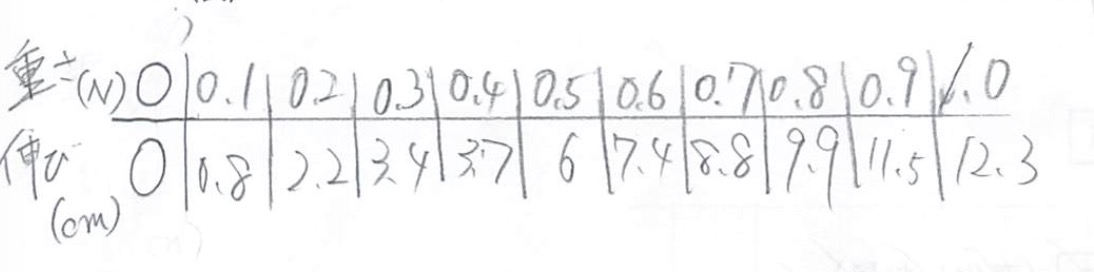
そして、得られたデータをグラフにしてみると……ここで面白いことが起きました。

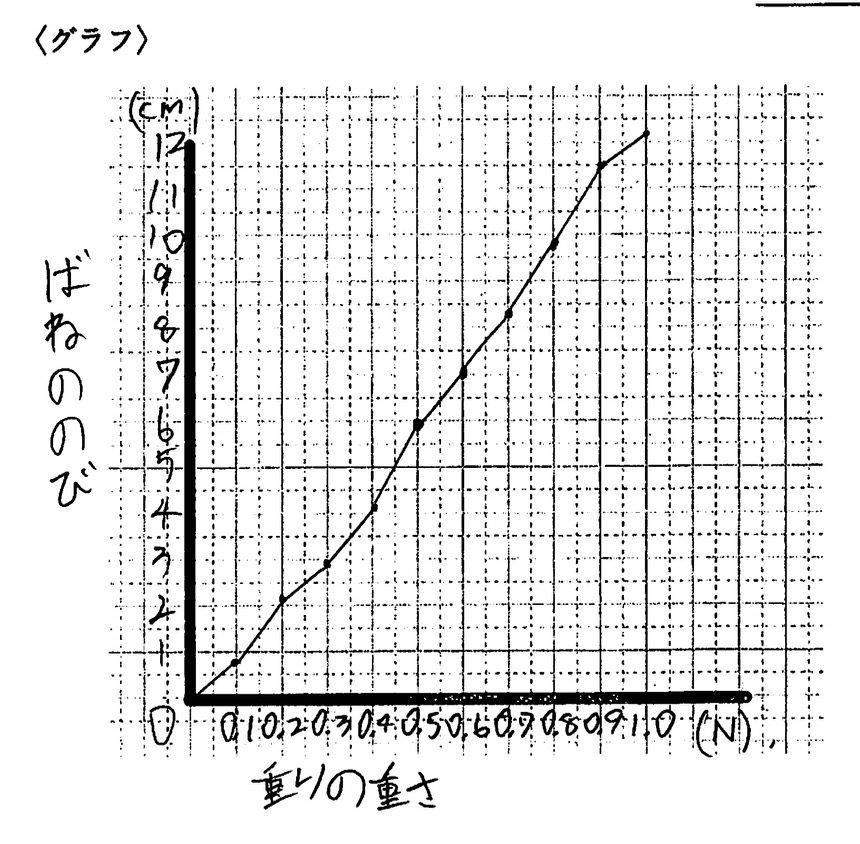
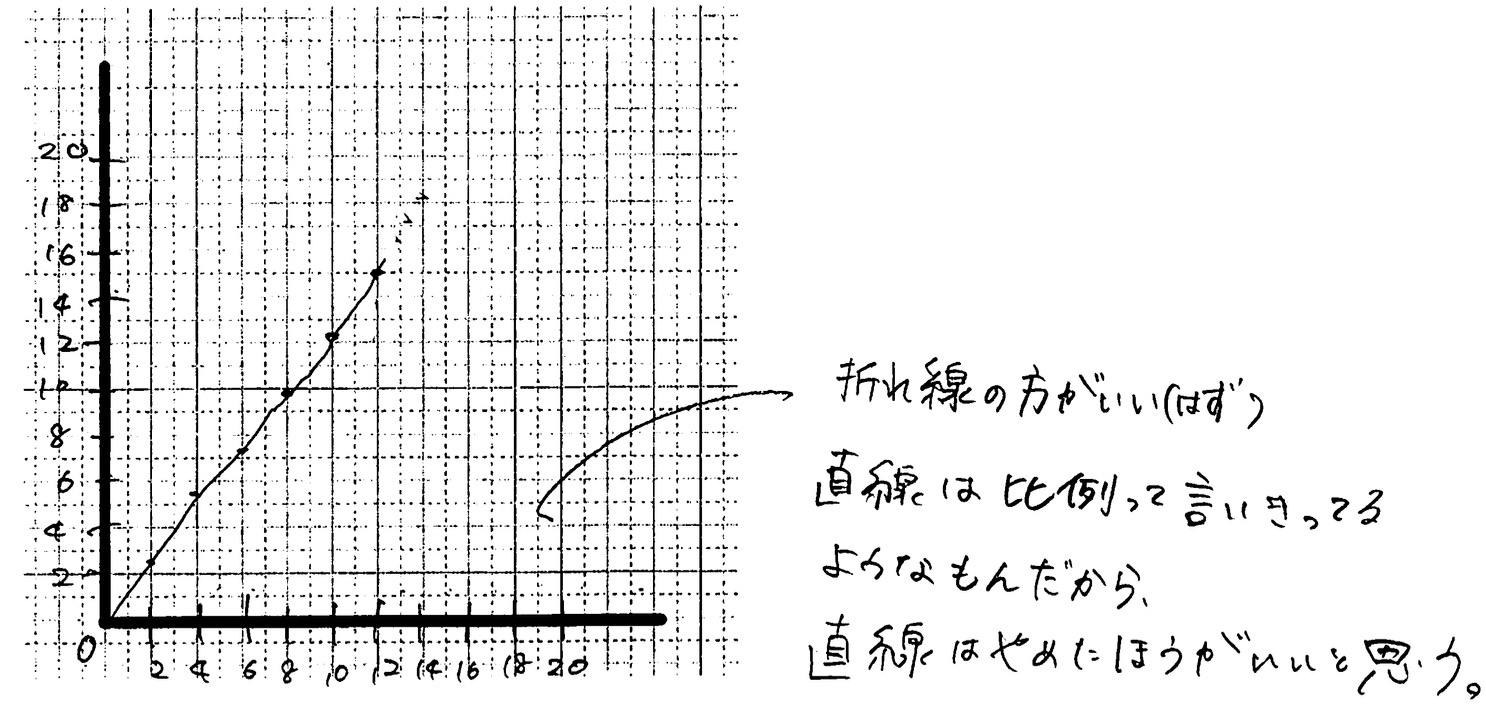
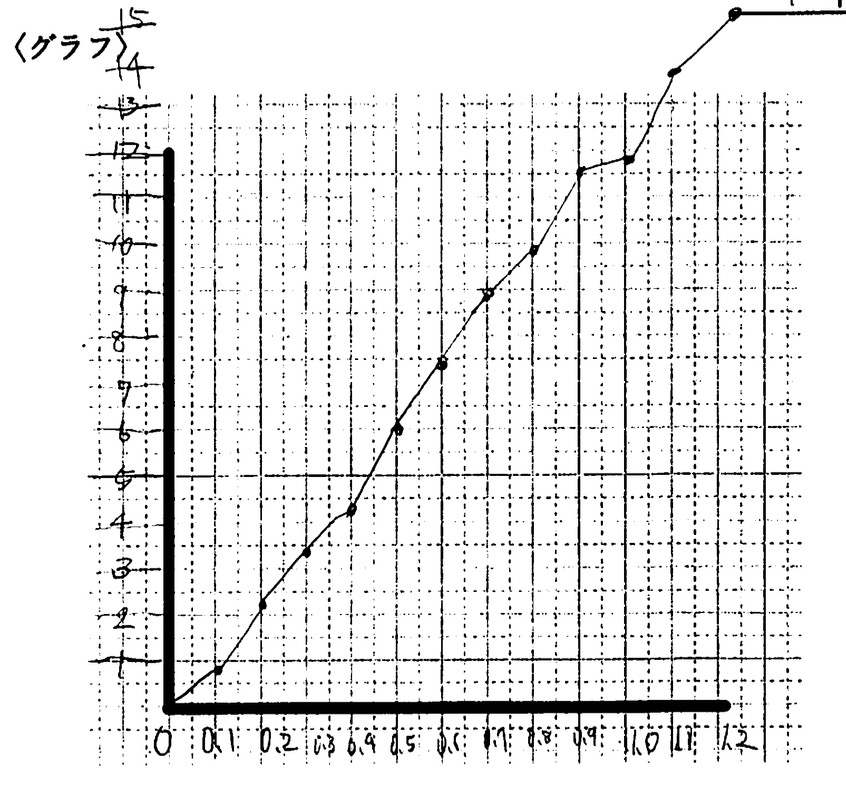
多くの班は、測定した点を定規で几帳面に結んで「折れ線グラフ」にしました。またある少数の班は、点と点の真ん中を通るような「直線」を引こうと試みました。教師が「こうしなさい」と言わなかったため、教室には「多様なグラフ」が生まれたのです。

その後、他の班のグラフを見に行く時間を設けました。「あ、あの班は直線を引いてる！」「なんであそこは折れ線なんだろう？」自分たちの結果と比べることで、生徒たちは赤ペンを片手に、自分たちのグラフに修正や気づきを書き加えていきます。正解を教わるのではなく、対話を通して自分たちの力で最適解に近づこうとする姿。これこそが、協働的な学びの真骨頂です。

点をつなぐのではなく、真実の線を探す

最後の授業では、みんなが作ったグラフをもとに、「科学的に正しいグラフとは何か」を議論しました。ここで、理科（物理学）におけるとても大切な考え方を共有しました。それは、「実験データには必ず誤差が含まれる」ということです。

点をそのままつなぐ折れ線グラフは、実は「誤差」まで正直に記録してしまっています。一方で、点のばらつきを均すように引いた「一本の直線」は、目の前の小さな誤差を無視して、その背後にある「自然界のルール（規則性）」を見つけ出そうとする行為なのです。

「直線を引くことで、測っていない場所の数値も予測できるよね」 「これが、ロバート・フックが見つけた『フックの法則』なんだよ」

生徒たちの表情が変わったのはこの瞬間でした。「なるほど、だから直線を引くのか！」という納得感。ただ単に「比例します」と暗記するのとは違い、自分たちの手で悩みながらデータを処理したからこそ、法則の意味がスッと心に落ちたようでした。

教師は「教える人」から「旅の仲間」へ

この3時間の授業を通して、私は「先生」というよりも、生徒と一緒に悩み、考える「同伴者」でありたいと強く感じました。

「失敗してもいいからやってみよう」「そのグラフ、どうしてそう引いたの？」と問いかけながら、生徒が試行錯誤する横で一緒に頭を捻る。教師が敷いたレールの上を走らせるのではなく、彼らが藪を切り開いていく後ろを、灯りを持ってついていくような感覚です。

科学の面白さは、正解をすぐに知ることではなく、不思議だなと思う現象の中に、美しい法則を見つけ出す過程にあります。これからも、生徒たちと一緒に科学の森を探検していきたいと思います。

お問い合わせ・ご依頼について

科学の不思議やおもしろさをもっと身近に！自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください！
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼（執筆・講演・実験教室・TV監修・出演など）はこちら
・記事の更新情報はXで配信中！

科学のネタチャンネルでは実験動画を配信中！