【Tietovisa】Kun porkkana katkaistaan tasapainokohdasta, kumpi on raskaampi? – Voiman momentti vihannesten avulla
Hei, olen tiedevalmentaja Ken Kuwako. Minulle jokainen päivä on kokeilu.
Meidän intuitiomme saattaa toisinaan joutua fysiikan lakien huijaamaksi. Kuvittelepa eteesi porkkana, joka roikkuu täydellisessä tasapainossa narun varassa. Jos leikkaisit porkkanan kahtia juuri siitä kohdasta, missä naru on, eikö kumpikin puoli painaisikaan yhtä paljon? Todellisuudessa tässä arkisessa tilanteessa piilee kiehtova fysiikan salaisuus. Tänään esittelen teille pienen pähkinän purtavaksi: fysiikkavisan! Pohtikaapa tätä yhdessä kanssani.
Tässä tulee päivän kysymys! Ta-daa!
Ripustamme porkkanan naruun alla olevan kuvan osoittamalla tavalla. Voitte yrittää kuvitella tilanteen mielessänne.

Porkkana saatiin tasapainoon siten, että naru kiinnitettiin hieman keskikohdan oikealle puolelle, eli porkkanan paksumpaan päähän. Nyt tulee varsinainen kysymys: Jos leikkaisit porkkanan veitsellä tasan tästä narun kohdasta kahtia, kumpi puoli olisi painovaltiaampi? Vasen (ohut pää) vai oikea (paksu pää)?

Mietippä hetki. Mikä on arvauksesi? Katsotaanpa sitten vastaus. Vastaus ja selitys löytyvät tästä videosta:
Uskomatonta mutta totta! Paino ei jakaudu tasan.
Todellisuudessa puolet eivät paina yhtä paljon! Toinen puoli on selvästi raskaampi. Yllätyitkö? Tämä on klassinen fysiikan tehtävä, joka hämmentää monia. Mutta miksi painoero syntyy? Avainsana on voiman momentti.
Kun punnitsemme puolet, tulos on seuraava:
Paksu puoli:

68 g
Ja ohut puoli: 
56 g
Kyllä vain, paksumpi puoli on painavampi!
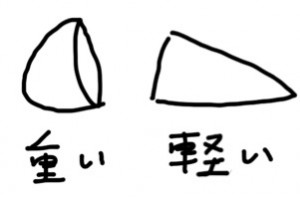
Paksu puoli on painava ja ohut puoli kevyempi.
Miten tämä on mahdollista? Ratkaistaan arvoitus hieman matemaattisemman ajattelun avulla.
Mikä on voiman momentti?
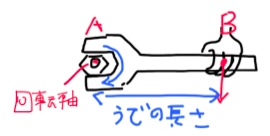
Kuvittele tilanne, jossa yrität kääntää tiukassa olevaa mutteria jakoavaimella. Jotta saisit mahdollisimman suuren vääntövoiman, mistä kohtaa tartut avaimeen? Tartut varmasti vaistomaisesti jakoavaimen varren päähän. Mitä kauempana pyörimisakselista (mutterista) olet, sitä vähemmällä voimalla saat aikaan suuren vääntövaikutuksen. Tätä ilmiötä kutsutaan momentiksi. Kaavana se näyttää tältä:
M = F × L
Momentti = Voima × Varren pituus
Tämä kaava on erittäin tärkeä! Painon (voiman) lisäksi etäisyys keskipisteestä (varren pituus) ratkaisee sen, kuinka suuri ”pyöritysvaikutus” syntyy.
Kun momentit ovat tasapainossa
Rakennetaanpa simppeli mobiili kevyestä rimasta ja kahdesta samanpainoisesta punnuksesta. Jos kiinnitämme narun täsmälleen riman keskelle, se pysyy suorassa.
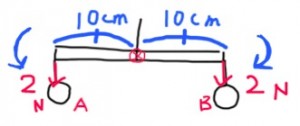
Tässä tilanteessa narun kohdalta laskettu momentti on kummallakin puolella sama:
Vasen punnus: 2N × 10cm = 20 Ncm (vastapäivään) Oikea punnus: 2N × 10cm = 20 Ncm (myötäpäivään)
Kun myötä- ja vastapäivään vaikuttavat momentit ovat yhtä suuret, esine pysyy paikallaan liikahtamatta. Tätä kutsutaan momenttitasapainoksi.
Mitä tapahtuu, jos punnukset ovat eripainoisia?
Siirrytäänpä lähemmäs porkkanatilannetta. Ripustetaan rimaan kaksi eri painoista palloa: 6 Newtonin painoinen ja 2 Newtonin painoinen pallo. Jotta rima pysyisi tasapainossa, narua on siirrettävä kauemmas keskikohdasta, lähemmäs painavampaa palloa.
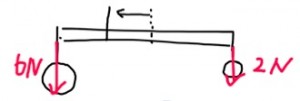
Tasapaino löytyy tästä kohdasta:
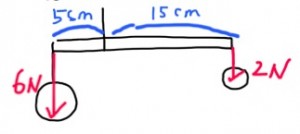
Vasen puoli: 6N × 5cm = 30 Ncm Oikea puoli: 2N × 15cm = 30 Ncm
Momentit ovat taas tasan! Mutta jos leikkaamme riman narun kohdalta, on selvää, että vasen puoli (6N) on huomattavasti painavampi kuin oikea (2N).
Porkkana-arvoitus ratkeaa!
Palataanpa vielä takaisin alkuperäiseen porkkanaan.
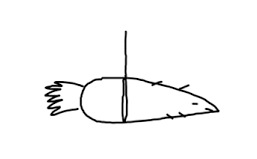
Porkkana oli tasapainossa, kun naru oli hyvin lähellä paksun pään ”painopistettä”. Tilanne on täsmälleen sama kuin 6 Newtonin ja 2 Newtonin kokeessamme.

Koska ohut pää on pitkä, pienikin paino riittää synnyttämään suuren momentin (vääntövaikutuksen). Paksu pää taas on lähellä narua, joten se tarvitsee paljon enemmän painoa kyetäkseen vastaamaan toisen puolen vääntöön. Vastaus on siis: paksu puoli on raskaampi! Voimien suhde näyttää kutakuinkin tältä:
Kun katsot maailmaa fysiikan linssien läpi, huomaat, että jopa ruokakaupan vihannesosastolta löytyy kauniita matemaattisia yhtälöitä ja tasapainon harmoniaa. Lisää mielenkiintoisia pähkinöitä löydät Tiedekokeiden oppikirjastani. Käy ihmeessä kurkkaamassa!
Ota yhteyttä ja tilaa tiedettä kotiisi!
Tuo fysiikan ihmeet ja oivaltamisen ilo osaksi arkeasi! Olen koonnut helppoja ja hauskoja kokeita, joita voit kokeilla kotona. ・Tiedonjyviä-blogin sisältö on nyt julkaistu kirjana! Lue lisää täältä. ・Lue lisää tiedevalmentaja Ken Kuwakosta täältä. ・Yhteydenotot ja tilaukset (artikkelit, luennot, tiedepajat, TV-konsultointi jne.) täältä. ・Seuraa uusimpia päivityksiä X-palvelussa!
![]() Tiedevinkit-kanavalta löydät lisää kokeiluvideoita!
Tiedevinkit-kanavalta löydät lisää kokeiluvideoita!
2月のイチオシ実験!梱包材で遊ぼう!
- 静電気の時期になってきました。子供と一緒に梱包材で盛り上がろう!→ やめられなくなる!静電気実験20
 体中に梱包材をはりつけてみよう!
体中に梱包材をはりつけてみよう!
テレビ番組等・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師等・ショー・その他お知らせ
- 2/20(金)「生徒の進学希望実現支援事業」研究授業@福井県立若狭高等学校 講師
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) サイエンスショー予定
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。