Minne theta (θ) oikein menee? Piirustustemppu selkeyttää asian! (Sairaanhoito ja lukion fysiikka yhdistyvät: kertomus voimien hajottamisesta)

Terveisin Ken Kuwako, tiedekouluttaja. Minulle jokainen päivä on kokeilu.

Sairaanhoitajaopiskelijatkin pulassa!? Opi fysiikkaa hauskasti tukiopetuksen avulla!

Hei kaikki, oletteko kuulleet tukiopetuksesta (remedial education)? Yksinkertaisesti selitettynä se on opetusta, jonka tarkoitus on vahvistaa yliopisto-opinnoissa vaadittavia perustaitoja. Erityisesti hoitoalalla monet opiskelijat kamppailevat fysiikan kanssa, ja juuri heitä varten kirjoitin oppikirjan nimeltä ”Ymmärrä fysiikan perusteet” (kustantaja Nanzando).

Mutta miksi hoitotyössä tarvitaan fysiikkaa, saatatte miettiä. Totuus on, että fysiikan osaamisesta on valtavasti hyötyä hoitajan työssä. Esimerkiksi potilaan avustamisessa käytettävä ergonomia (body mechanics) ja infuusiolaitteiden paineensäätö ovat tilanteita, joissa fysiikkaa sovelletaan yllättävän usein.

Saan usein sekä valmistuneilta että nykyisiltä hoitoalan opiskelijoilta saman kysymyksen. Kuulen sen usein myös lukiossa opettaessani, joten vastaus saattaa auttaa teitäkin!

”Miksi painovoiman kaltevan tason suuntaiseen komponenttiin liittyy sinθ?”

Tämä on klassinen kysymys, joka liittyy voimien jakamiseen komponentteihin. Erityisesti kun tarkastellaan kaltevalla tasolla olevaan kappaleeseen vaikuttavia voimia, sini ja kosini menevät helposti sekaisin. Kerrankin eräs opiskelija tuli luokseni harjoituskokeen kanssa ja pyysi apua juuri tähän. Kuvitellaanpa seuraava tilanne:

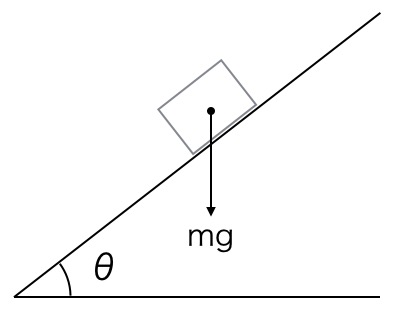
Kappaleen liike kaltevalla tasolla

Kun jaamme kaltevalla tasolla olevaan kappaleeseen vaikuttavan painovoiman komponentteihin, saamme tason suuntaisen ja tasoa vastaan kohtisuoran komponentin. Tason suuntaiseen komponenttiin liittyy sinθ, mutta miksi? On totta, että kuviosta on vaikea heti nähdä, mihin kulma θ sijoittuu voimakolmiossa.

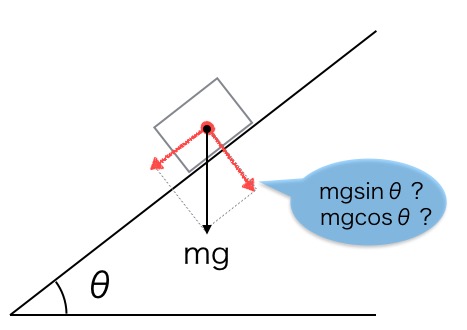
Mihin θ sijoittuu?

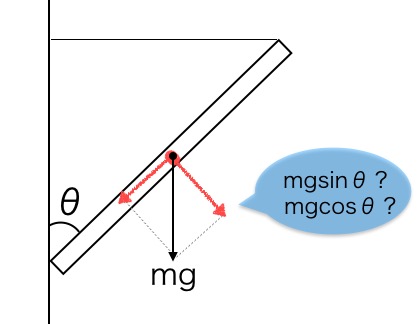
Sini vai kosini?

Piirretään ensin kuva uudelleen äärimmilleen vietynä!

Tällaisissa tapauksissa käytetään yleensä kolmioiden yhdenmuotoisuutta, mutta minä suosittelen piirtämään annetun kuvan uudelleen äärimmäisillä arvoilla. Kokeillaan esimerkiksi pienentää kaltevan tason kulmaa äärimmäisen pieneksi.

 

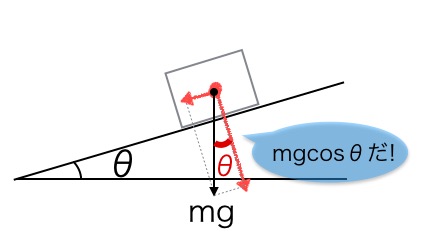
　Silloin voimme arvata, että painovoiman komponentteihin jaetun kuvion terävin kulma on θ. Voimme myös piirtää kuvan uudelleen suurentamalla θ:ta äärimmilleen. Esimerkiksi aiemmassa voimamomomenttia koskevassa tehtävässä voimme piirtää kuvion suurella θ:lla.

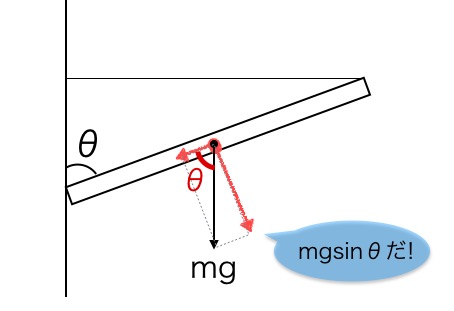
Nyt θ:n paikka on täysin selvä, eikö niin? Tällä tavoin, jos tehtävänannossa on epäselvä, noin 45 asteen kulmalla piirretty kuvio, kannattaa se piirtää uudelleen käyttäen äärimmäisiä kulmia (kuten 30 tai 60 astetta). Kulman θ siirtyminen on tällöin helpompi hahmottaa kuin pelkän yhdenmuotoisuussäännön avulla.

Hyödynnä yhdenmuotoisuutta ja kulmien suhteita

Tietenkin on myös tärkeää ymmärtää teoria sille, miksi θ on juuri siinä paikassa. Esimerkiksi kaltevan tason tapauksessa voimme tarkastella kahta yhdenmuotoista suorakulmaista kolmiota löytääksemme θ:n paikan.

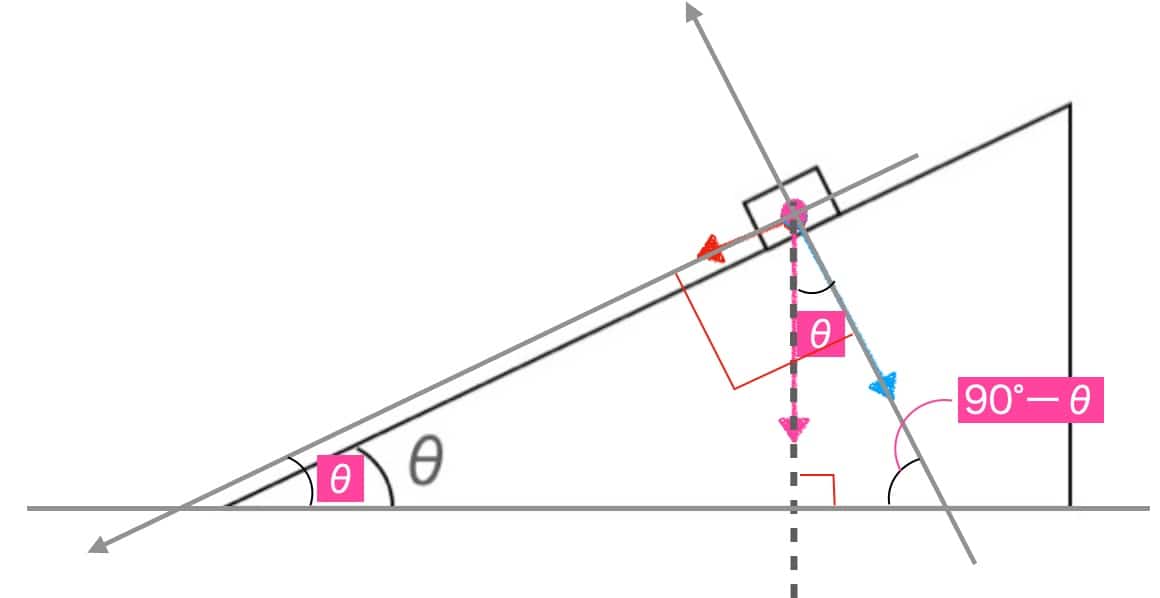
Näin voimme ilmaista voimien suuruudet.

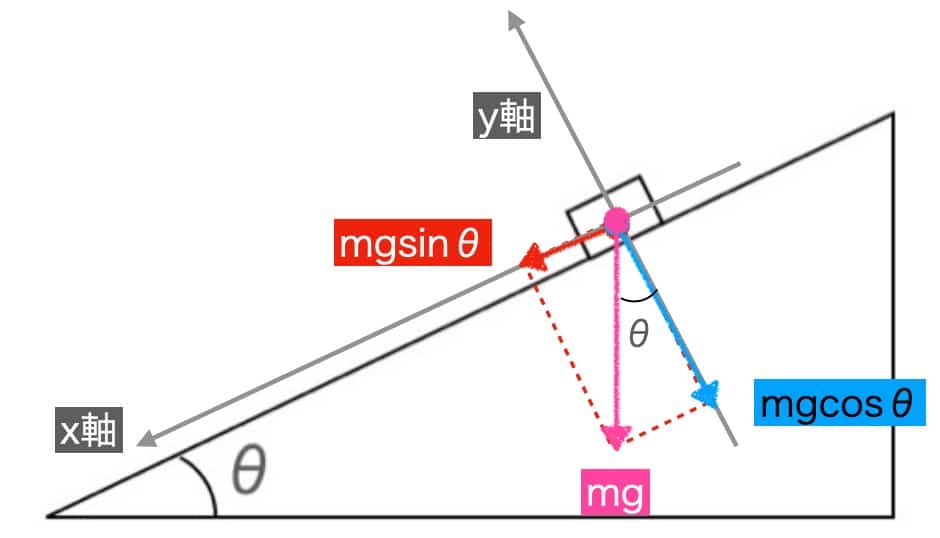
Hyödynnämme siis kolmioiden yhdenmuotoisuutta tai samankohtaisten kulmien ominaisuuksia yhdensuuntaisten suorien kanssa.

Ota yhteyttä tai pyydä tarjous

Tuo tieteen ihmeet ja hauskuus lähemmäksi! Tarjoan selkeitä ohjeita ja vinkkejä hauskoihin tiedekokeisiin, joita voit tehdä kotona. Kokeile hakua ja löydä lisää!
・Lisätietoa minusta, Ken Kuwakosta, löydät täältä.
・Teen erilaisia toimeksiantoja (kirjoitustyöt, luennot, tiedekerhot, TV-konsultointi, esiintymiset yms.). Pyydä tarjous täältä.
・Seuraa uusimpia päivityksiä X:ssä!

Tiedekanavallani julkaisen videoita kokeista!