Miksi se ei kaadu? Fysiikan laeilla rakennettu “ääretön kirnatorni”

Tervehdys, olen tiedevalmentaja Ken Kuwako! Joka päivä on uusi kokeilu.

Kirja roikkuu yli puolet pituudestaan pöydän reunan yli, mutta se ei putoa… Se näyttää silmänkääntötempulta, mutta todellisuudessa kyseessä on puhdas tiede. Tänään tutkimme fysiikan lakeja ja rakennamme oman maagisen tornin, joka pysyy pystyssä täydellisen tasapainon ansiosta.

Tämän haasteen avain on lukiofysiikasta tuttu käsite: voiman momentti. Kuulostaa ehkä monimutkaiselta, mutta ei hätää – se on yhtä intuitiivista kuin leikkipuiston keinulaudalla olo. Ratkaisemme tämän mysteerin kahden tärkeän käsitteen, painopisteen ja pyörimisakselin, avulla.

Aluksi perusteet: Mikä on painopiste?

Jokaisella esineellä on painopiste. Se on kohta, johon esineen koko painon voidaan ajatella keskittyvän. Saadaksesi tuntumaa tähän, kokeillaan ensin kahdella kirjalla. Työnnä ylintä kirjaa (1. kirja) varovasti reunan yli niin pitkälle kuin mahdollista ilman, että se putoaa.

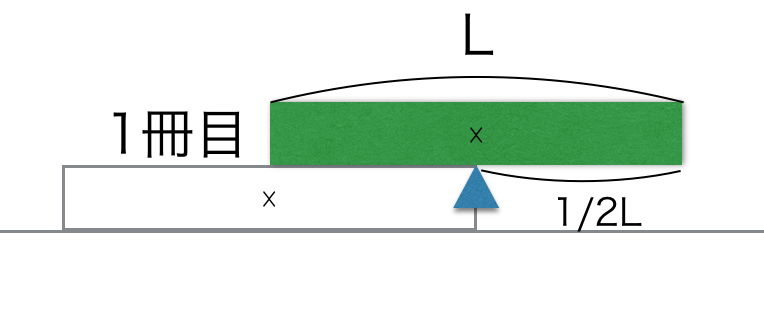
Mitä huomaat? Kirja pysähtyy kuin seinään juuri silloin, kun puolet siitä on tyhjän päällä. Jos kirjan pituus on L, sen painopiste on tasan puolivälissä eli kohdassa 1/2 L. Kriittinen piste, jossa kirja ei vielä putoa, on juuri siinä, missä ylemmän kirjan painopiste on alemman kirjan reunan (pyörimisakselin) kohdalla. Eli voit työntää kirjaa ulos 1/2 L verran ja se pysyy vielä vakaana.

Seuraava taso: Voiman momentti ja tasapaino
Lisätään peliin kolmas kirja. Nyt alkaa varsinainen haaste! Käsitellään ensimmäistä ja toista kirjaa yhtenä kokonaisuutena ja etsitään kohta, jossa ne pysyvät juuri ja juuri kolmannen kirjan päällä.

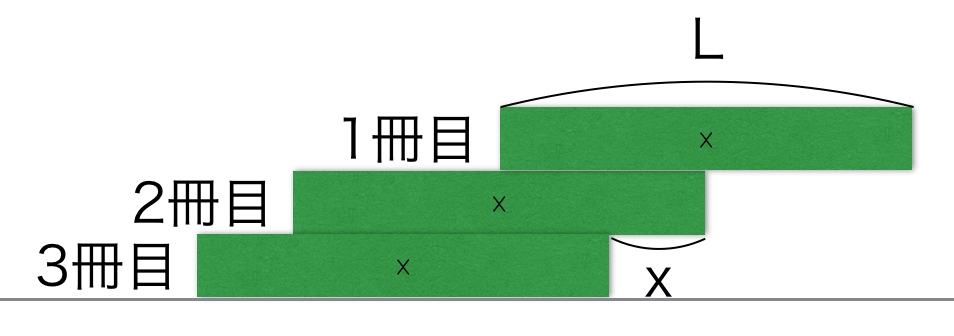
Tässä kohtaa mukaan astuu voiman momentti. Se kuvaa voiman kykyä aiheuttaa pyörimistä ja se lasketaan kaavalla: etäisyys tukipisteestä × voiman suuruus (paino). Tämä on sama periaate kuin keinulaudalla: kevyempikin lapsi voi tasapainottaa painavamman, jos hän istuu kauempana keskipisteestä.

Kun katsomme kolmannen kirjan reunaa pyörimisakselina, kirjat eivät putoa, jos vasemmalle vääntävä voima (2. kirjan paino) ja oikealle vääntävä voima (1. kirjan paino) ovat tasapainossa.

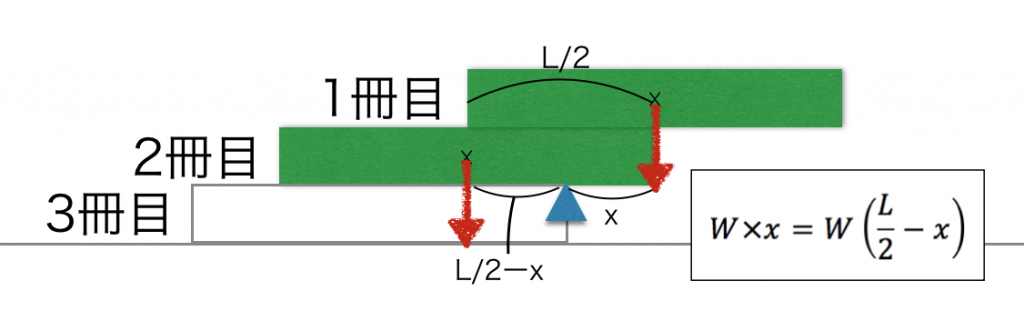
Kun laskemme tämän tasapainon yhtälön avulla, huomaamme, että siirtymä x on…

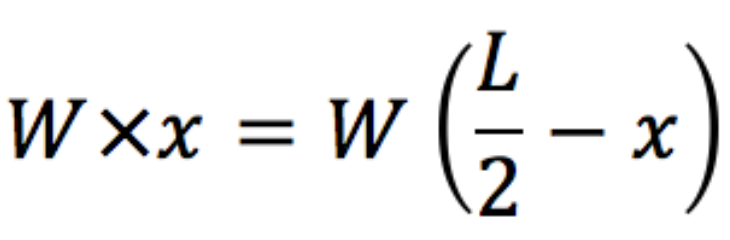
Uskomatonta kyllä, se on 1/4 L. Mitä tapahtuukaan, jos jatkamme pinoamista?

Kaunis laki ja hämmästyttävä lopputulos
Pohditaan tilannetta neljällä kirjalla.

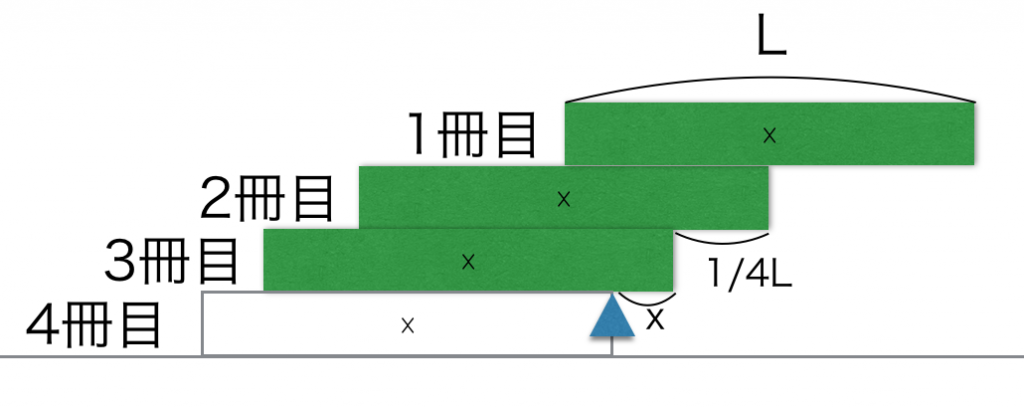
Otetaan alimman kirjan reuna pyörimisakseliksi ja lasketaan päällä olevien kolmen kirjan momenttien tasapaino.

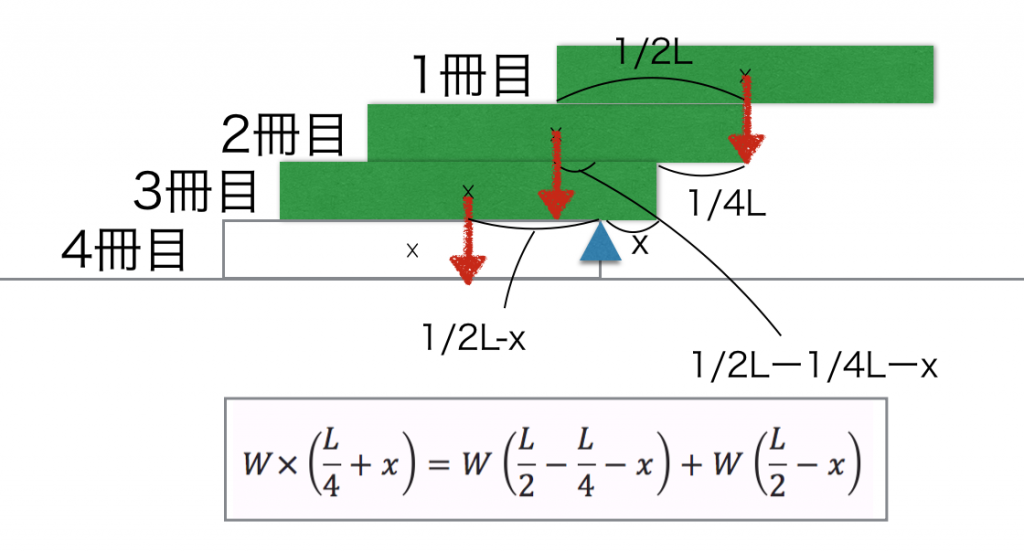
Yhtälön ratkaisu antaa…

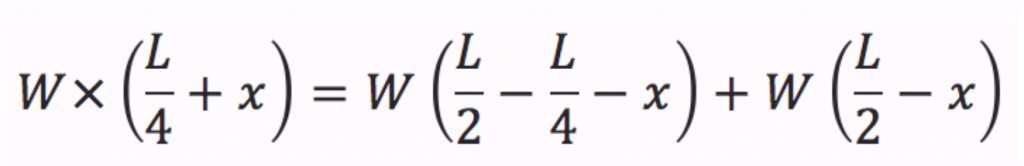
Tällä kertaa tulos on 1/6 L.

Tarkastellaanpa tuloksia järjestyksessä. Ylhäältä alkaen maksimisiirtymät ovat:

1/2 L, 1/4 L, 1/6 L, …

Huomaatko kauniin säännönmukaisuuden? Tämän logiikan mukaan viidennen kirjan siirtymä olisi 1/8 L ja kuudennen 1/10 L!

Kun tätä jatketaan, syntyy tällainen torni:

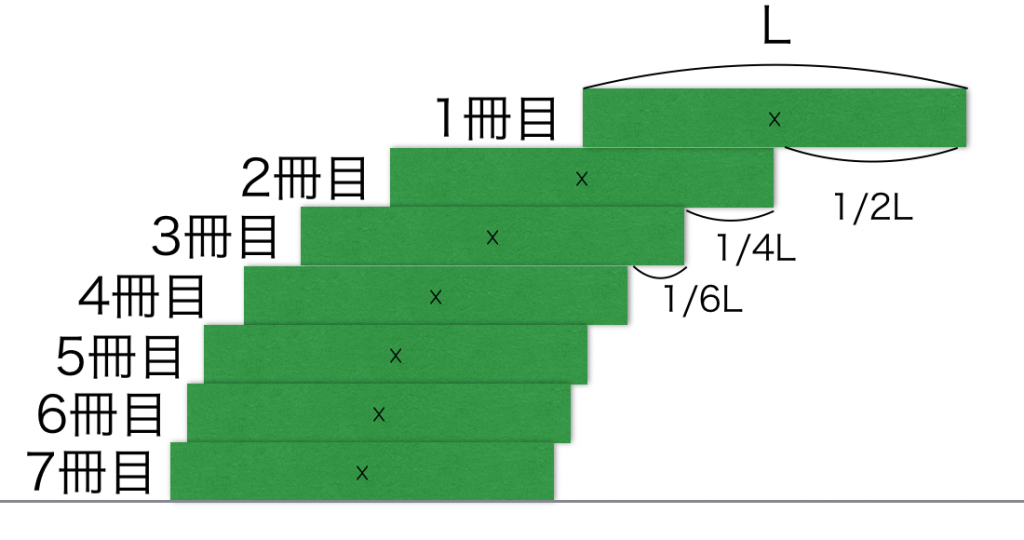
Ylin kirja on kokonaan alimman kirjan ulkopuolella. Ja tässä tulee tieteen todella mielenkiintoinen osuus: Tämä sarja (1/2 + 1/4 + 1/6 + …) tunnetaan matematiikassa harmonisen sarjan sukulaisena, ja on todistettu, että tämän summan arvo kasvaa äärettömiin. Eli teoreettisesti, jos pinoat äärettömän määrän kirjoja, voit ulottaa tornin kuinka kauas tahansa!

Kokeile itse!
Teorian jälkeen on aika siirtyä käytäntöön. Onnistumisen salaisuus on käyttää samanlaisia ja samanpainoisia kirjoja tai puupalikoita. Kokeilin itse ensin paksuilla puupalikoilla.

Sitten testasin kirjoilla.

Ensin perusmalli: puolikas siirtymä. Tämä on helppoa!

Viiden kirjan haaste. Avain on lyhentää siirtymää mitä alemmas mennään, aivan laskujen mukaan. Rajan etsiminen on vaikeaa, mutta juuri siksi niin hauskaa!

Onnistuin näin pitkälle! Tämä vaatii keskittymistä ja hengen pidättämistä kirjaa laskiessa.

Kokeilin myös puupalikoilla. Ne saattavat olla jopa helpompia pinota kuin kirjat.

Ensi silmäyksellä mahdottomalta tuntuva ilmiö selittyy täysin fysiikan tiedolla painopisteestä ja voiman momentista. Tasapainon rajojen etsiminen on loistava tapa kokea fysiikan lait käytännössä. Kokeile ihmeessä rakentaa oma tornisi kotoa löytyvillä kirjoilla tai palikoilla!

Yhteydenotot ja tiedustelut
Tuo tieteen ihmeet lähemmäksi arkeasi! Kerään sivuilleni selkeitä ohjeita hauskoihin kotikokeiluihin. Tutustu ja innostu! ・Lisätietoa ylläpitäjästä (Ken Kuwako) löydät täältä ・Yhteistyöpyynnöt (artikkelit, luennot, tiedepajat, TV-konsultointi jne.) täältä ・Seuraa uusimpia päivityksiä X-palvelussa!

Tiedekanavalla julkaistaan videoita kokeiluista!

３月のイチオシ実験！

• 押し花を作ろう！：梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。

テレビ番組・科学監修等のお知らせ

• 「月曜から夜更かし」（日本テレビ）にて科学監修・出演しました。
• 2月27日放送予定「チコちゃんに叱られる」（NHK）の科学監修しました。

書籍のお知らせ

• 1/27 『見えない力と遊ぼう！電気・磁石・熱の実験』（工学社）を執筆しました。
• サクセス15 ２月号にて「浸透圧」に関する科学記事を執筆しました。
• 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01）
• 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ

• 3/20（金）　日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第３セッション： 学習指導・教材（中学校）③　11:20-12:20
• 7/18（土）　教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
• 10/10（土）　秘密兵器「帯電ガン」が炸裂！ビリビリ！ドキドキ！静電気サイエンスショー＠千葉市科学フェスタ（午後予定）
• 各種SNS　X(Twitter)／instagram／Facebook／BlueSky／Threads

Explore

• 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
• 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
• Youtube…科学実験等の動画を配信しています。
• 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
• 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
• About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
• お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。