यह क्यों नहीं गिरता? भौतिकी के नियमों से बना “अनंत किताबों का टॉवर”
नमस्ते, मैं साइंस ट्रेनर केन कुवाको हूँ। मेरे लिए हर दिन एक नया प्रयोग है।
मेज के किनारे से आधी से ज्यादा बाहर निकली हुई किताब, फिर भी गिर नहीं रही है… यह किसी जादू जैसा लग सकता है, लेकिन इसके पीछे विज्ञान का एक गहरा रहस्य छिपा है। आज हम भौतिकी (Physics) के नियमों का इस्तेमाल करके, एक ऐसी जादुई मीनार बनाना सीखेंगे जो संतुलन की हर सीमा को चुनौती देती है।
इस चुनौती को समझने की कुंजी हाई स्कूल फिजिक्स का एक सिद्धांत है, जिसे ‘बल आघूर्ण’ (Moment of Torque) कहते हैं। नाम सुनकर घबराइए मत! इसे समझना उतना ही आसान है जितना पार्क में सी-सॉ (झूला) झूलना। हम ‘द्रव्यमान केंद्र’ (Center of Gravity) और ‘घूर्णन अक्ष’ (Axis of Rotation) जैसे दो जरूरी शब्दों की मदद से इस दिलचस्प घटना की गुत्थी सुलझाएंगे।
सबसे पहले बुनियादी बात: यह ‘द्रव्यमान केंद्र’ क्या है?
हर वस्तु का एक ‘द्रव्यमान केंद्र’ होता है। यह वह बिंदु है जहाँ वस्तु का पूरा भार केंद्रित माना जाता है। इसे समझने के लिए, आइए सिर्फ दो किताबों के साथ शुरुआत करें। ऊपर वाली किताब को नीचे वाली किताब के ऊपर धीरे-धीरे खिसकाएं, तब तक जब तक वह गिरने ही वाली न हो।
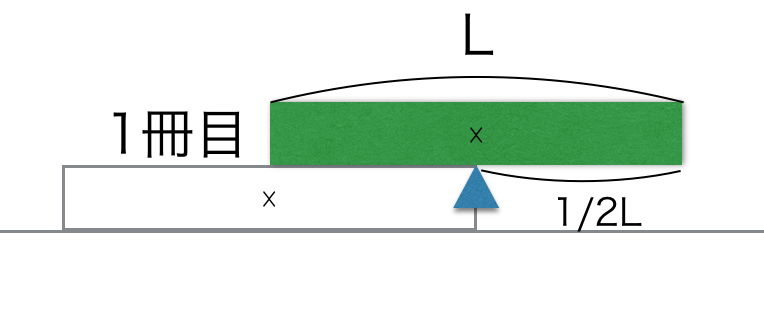
क्या आपने देखा? जैसे ही किताब का आधा हिस्सा बाहर निकलता है, वह वहीं रुक जाती है। अगर किताब की लंबाई L है, तो उसका द्रव्यमान केंद्र ठीक बीच में, यानी किनारे से 1/2L की दूरी पर होता है। किताब के न गिरने की आखिरी सीमा वह है जहाँ पहली किताब का द्रव्यमान केंद्र ठीक नीचे वाली किताब के किनारे (घूर्णन अक्ष) के ऊपर होता है। यानी 1/2L तक बाहर निकालने पर भी संतुलन बना रहता है।
स्तर बढ़ाएं: सी-सॉ की तरह ‘बल आघूर्ण’ से संतुलन खोजें
अब किताबों की संख्या बढ़ाकर तीन करते हैं। असली खेल यहीं से शुरू होता है! अब हम पहली और दूसरी किताब को एक जोड़ी मानेंगे और देखेंगे कि वे तीसरी किताब पर कितनी बाहर निकल सकती हैं।
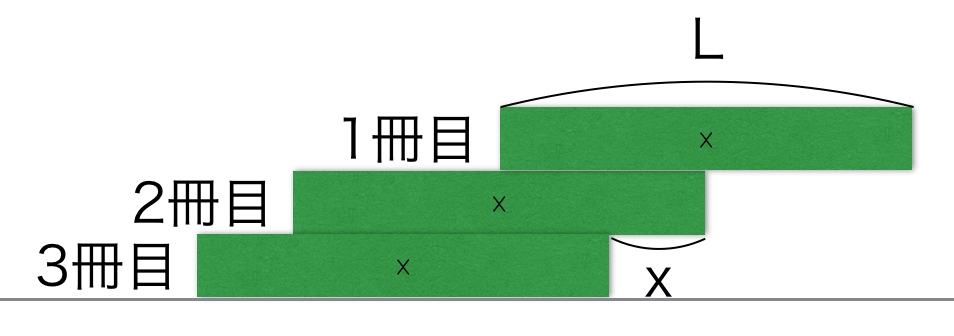
यहाँ काम आता है ‘बल आघूर्ण’। यह वह बल है जो किसी वस्तु को घुमाने की कोशिश करता है। इसका हिसाब ‘धुरी से दूरी × भार’ से लगाया जाता है। ठीक वैसे ही जैसे सी-सॉ पर एक हल्का बच्चा भी अगर धुरी से दूर बैठे, तो वह भारी बच्चे को संतुलित कर सकता है।
नीचे दिए गए चित्र में, तीसरी किताब के किनारे से देखते हुए, बाईं ओर झुकाने वाला बल और दाईं ओर झुकाने वाला बल जब बराबर हो जाते हैं, तो किताब नहीं गिरती।
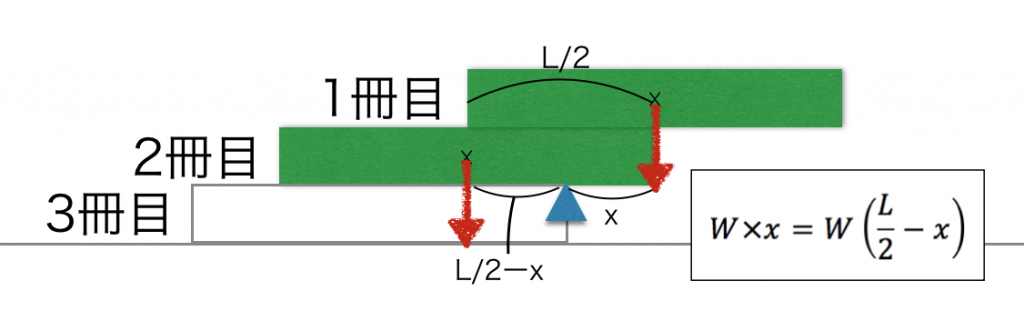
जब हम इस संतुलन को गणितीय सूत्र से हल करते हैं, तो खिसकाई जा सकने वाली दूरी x निकलती है…
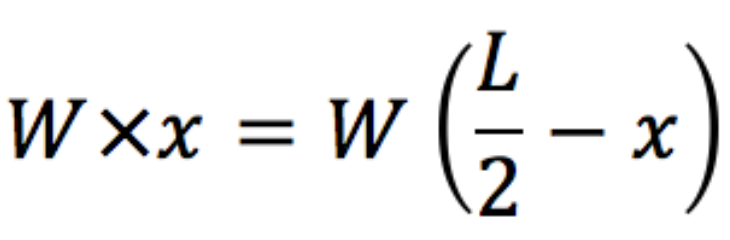
हैरानी की बात है कि यह दूरी 1/4L आती है। अगर हम किताबें बढ़ाते जाएं तो क्या होगा?
एक खूबसूरत नियम और चौंकाने वाला परिणाम
अब चार किताबों के साथ यही प्रयोग दोहराते हैं।
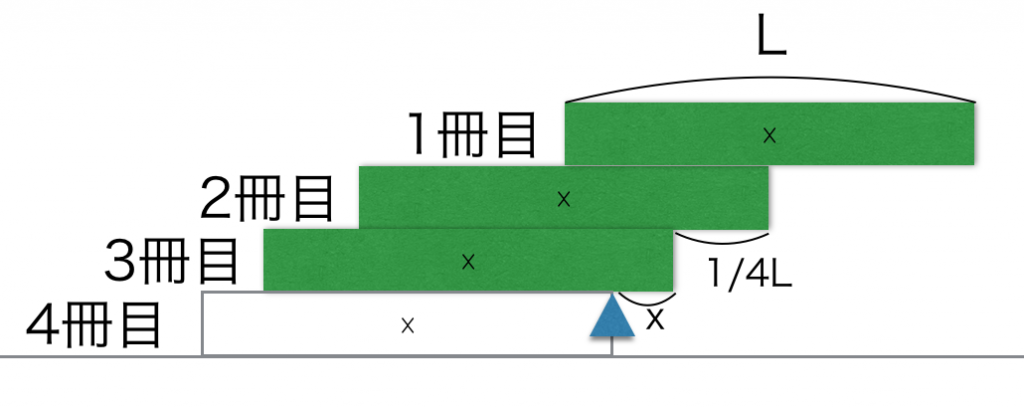
सबसे नीचे वाली किताब के किनारे को आधार मानकर ऊपर की तीन किताबों के बल आघूर्ण का संतुलन देखते हैं।
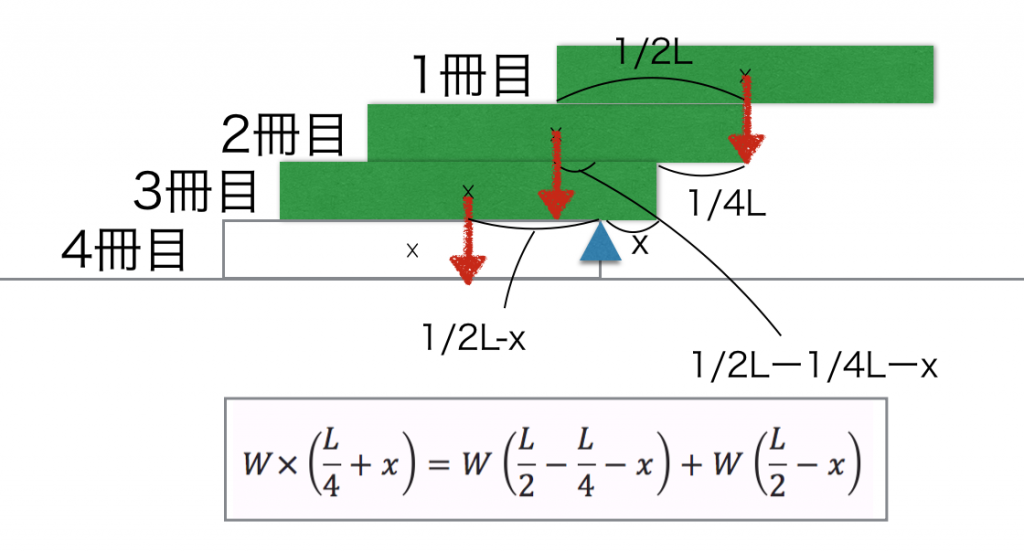
इस समीकरण को हल करने पर…
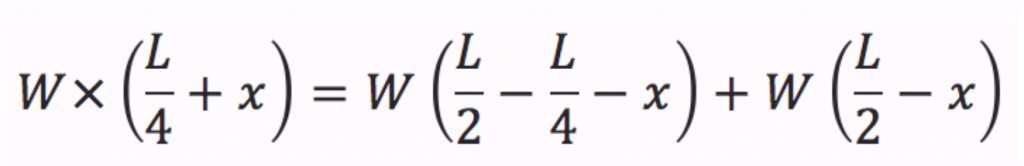
इस बार दूरी 1/6L निकली।
जरा इन नतीजों पर गौर करें। ऊपर से नीचे की ओर किताबों को बाहर खिसकाने की लंबाई कुछ इस तरह है:
1/2L, 1/4L, 1/6L, …
क्या आपको इसमें एक सुंदर पैटर्न दिख रहा है? इस नियम के हिसाब से पांचवीं किताब को 1/8L और छठी किताब को 1/10L तक खिसकाया जा सकता है!
इस तरीके से बनी मीनार कुछ ऐसी दिखेगी:
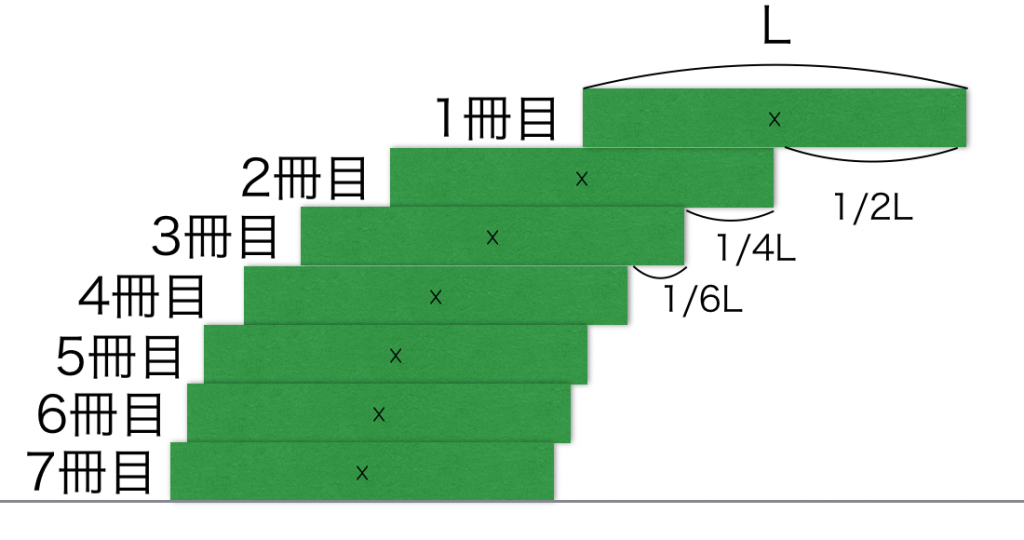
सबसे ऊपर वाली किताब, सबसे नीचे वाली किताब के आधार से पूरी तरह बाहर निकल चुकी है। और अब आता है विज्ञान का सबसे मजेदार मोड़। गणित में इस श्रृंखला (1/2 + 1/4 + 1/6 + …) को ‘हार्मोनिक सीरीज’ का हिस्सा माना जाता है। यह साबित हो चुका है कि इन संख्याओं का जोड़ अनंत (Infinite) तक जा सकता है। यानी सैद्धांतिक रूप से, अगर आप अनंत किताबें जमा करें, तो आप मीनार को मेज से कितनी भी दूर तक बढ़ा सकते हैं!
चलिए, अब खुद करके देखें!
थ्योरी समझने के बाद इसे आजमाना तो बनता है। एक ही आकार और वजन की किताबें या लकड़ी के ब्लॉक इस्तेमाल करना सफलता का मंत्र है। मैंने पहले लकड़ी के गुटकों के साथ कोशिश की।


फिर मैंने किताबों के साथ प्रयोग किया।

पहले ‘आधा खिसकाने’ वाला बेसिक स्टेप। यह तो आसान है!
5 किताबों की चुनौती। खास बात यह है कि नीचे जाने पर खिसकाने की दूरी कम करते जाना है। बिल्कुल सही बैलेंस ढूँढना मुश्किल है, पर मजा भी उसी में है!

आखिरकार यहाँ तक सफलता मिली! इसके लिए गहरी एकाग्रता और थमी हुई सांसों की जरूरत होती है।

जो चीज देखने में जादुई लगती है, वह ‘द्रव्यमान केंद्र’ और ‘बल आघूर्ण’ जैसे भौतिकी के सिद्धांतों से समझी जा सकती है। संतुलन की सीमाओं को जानना भौतिकी को महसूस करने का एक शानदार मौका है। आप भी अपने घर पर किताबों या खिलौनों के ब्लॉक्स के साथ इस जादुई मीनार को बनाने की कोशिश जरूर करें!
संपर्क और पूछताछ
विज्ञान के रहस्यों और मजेदार पहलुओं को अपने करीब लाएं! मैं घर पर किए जा सकने वाले आसान प्रयोगों और उनके पीछे के विज्ञान को साझा करता रहता हूँ। अधिक जानकारी के लिए खोजें! ・ऑपरेटर केन कुवाको के बारे में यहाँ देखें ・विभिन्न अनुरोधों (लेखन, व्याख्यान, कार्यशाला, टीवी परामर्श आदि) के लिए यहाँ क्लिक करें ・लेटेस्ट अपडेट के लिए मुझे X (ट्विटर) पर फॉलो करें!
![]() मेरे YouTube चैनल पर प्रयोगों के वीडियो देखें!
मेरे YouTube चैनल पर प्रयोगों के वीडियो देखें!
3月のイチオシ実験!
- 押し花を作ろう!:梅や桜の花の押し花を作ってみましょう。特別なケースに入れると、長く保存できて、しおりにもなります。
テレビ番組・科学監修等のお知らせ
- 「月曜から夜更かし」(日本テレビ)にて科学監修・出演しました。
- 2月27日放送予定「チコちゃんに叱られる」(NHK)の科学監修しました。
書籍のお知らせ
- 1/27 『見えない力と遊ぼう!電気・磁石・熱の実験』(工学社)を執筆しました。
- サクセス15 2月号にて「浸透圧」に関する科学記事を執筆しました。
- 『大人のための高校物理復習帳』(講談社)…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり6刷となりました(2026/02/01)

- 『きめる!共通テスト 物理基礎 改訂版』(学研)… 高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・その他お知らせ
- 3/20(金) 日本理科教育学会オンライン全国大会2026「慣性の法則の概念形成を目指した探究的な学びの実践」について発表します。B会場 第3セッション: 学習指導・教材(中学校)③ 11:20-12:20
- 7/18(土) 教員向け実験講習会「ナリカカサイエンスアカデミー」の講師をします。お会いしましょう。
- 10/10(土) 秘密兵器「帯電ガン」が炸裂!ビリビリ!ドキドキ!静電気サイエンスショー@千葉市科学フェスタ(午後予定)
- 各種SNS X(Twitter)/instagram/Facebook/BlueSky/Threads
Explore
- 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
- 理科の教材… 理科教師をバックアップ!授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
- Youtube…科学実験等の動画を配信しています。
- 科学ラジオ …科学トピックをほぼ毎日配信中!AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
- 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
- About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
- お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。



