2025年9月4日 / Last updated : 2025年9月4日 桑子 研 Science

Terror of a 16m Drop, Explained by Science! A Mathematical Look at Splash Mountain: Disneyland Physics

I’m Ken Kuwako, your Science Trainer. Every day is an experiment.

Did you know you can calculate the speed of Splash Mountain using physics?

This article is also available on our radio show!

If I were to ask, “Who has ridden Splash Mountain at Tokyo Disneyland?”, almost everyone in the classroom would raise their hand. For students, Tokyo Disneyland is a “physical world” they’ve already experienced. On the other hand, if I ask, “Who has ridden FUJIYAMA?”, only about 10% would respond. It seems the bar for “thrill rides” is quite high.

But wait a minute. Did you know that Splash Mountain is one of the fastest rides at Tokyo Disneyland? Yes, that one where the log boats take a massive dive into a splashdown pool.

In fact, you can predict and calculate the speed of Splash Mountain using basic physics knowledge from middle and high school! It’s no longer just a “ride”—it’s a “teaching tool.” With that in mind, why don’t we take another look at Splash Mountain?

How High Is It, Really? Let’s Check the Stats!

The iconic drop scene of Splash Mountain. Just how high is that final plunge? According to the official guide, the maximum drop is 16 meters.

That’s about the height of a three-story school building! If you’ve never been on Splash Mountain, you can check out the drop in this video around the 7:00 mark. That’s a 16-meter drop.

Further research revealed these official stats:

Total Length: 850m
• Water Volume: 110 tons per minute
• Max Incline: 45 degrees
• Top Speed: 62 km/h

These numbers are just begging to be calculated by a physics enthusiast!

I Went and Collected Data Myself

I was so excited to test this myself that I snuck away during some free time on a school trip to ride Splash Mountain (it was almost a life-or-death mission, as I’m not a big fan of rides).

I discreetly brought along an altimeter and an accelerometer to collect data. The results confirmed that the drop was indeed around 16 meters.


Raw data and comparisons with other rides (Space Mountain, Big Thunder Mountain) are available in a separate article.

スプラッシュマウンテンの高度・加速度の一部始終を測って見た【ディズニーランド物理学】

Check it Out in a Video

If you’ve never been on Splash Mountain, be sure to check out the video below around the 7-minute mark. You might think “it doesn’t look so bad…” from the video, but the real experience is a whole different level of thrilling!

Now, Let’s Calculate! It’s Physics Time!

This is where science really shines. Splash Mountain doesn’t have an engine; it drops from its highest point using only the force of gravity. In a case like this, we can use the Law of Conservation of Energy to predict the speed based on the drop height.

■ Physics Formulas to Use

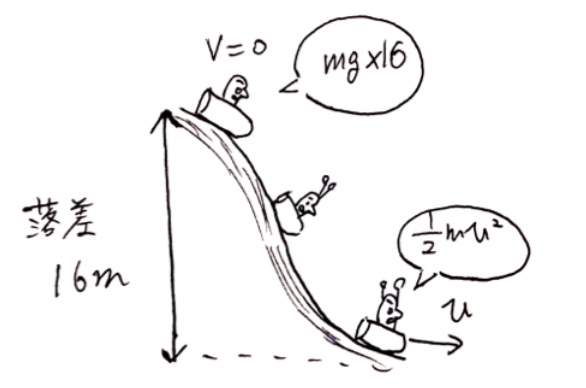
Potential Energy (mgh) = Kinetic Energy (½mv²)
→ Therefore,

v=√2gh

Where:
g = 9.8 m/s² (acceleration due to gravity)
h = 16 m (height)

Calculating this, we get:

v=√2times9.8times16
approx
√313.6
approx17.7m/s
→ Converting to km/h:

17.7
times3.6
approx63.7km/h
✅ Result: About 64 km/h!

This is almost identical to the official top speed of 62 km/h! Physics is incredible, isn’t it?

Key Takeaways for the Classroom!

• Since most students have ridden the ride, it’s a very smooth introduction.
• It’s a perfect real-world application of the Law of Conservation of Energy.
• Students can experience the “matching of feeling and theory,” which boosts their motivation to learn.

Similarly, we can use the same method to calculate the speed of FUJIYAMA at Fuji-Q Highland.

According to FUJIYAMA’s official website, the maximum drop is 70m and the top speed is 130 km/h.

Official FUJIYAMA Website (Fuji-Q Highland)

Let’s try calculating it using the Law of Conservation of Mechanical Energy. If we use 70 for ‘h’ in the formula we just used, we get:

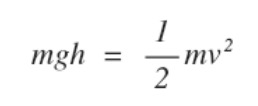
v=√(2×9.8×70)

v = 37 m/s, which converts to 133.2 km/h. That’s a very close value! How cool is that? But why are both Splash Mountain and FUJIYAMA’s actual top speeds slightly lower than the theoretical values? Why do you think that is?

External Forces at Play… but Why?

In rides like roller coasters or pendulums, “mechanical energy (kinetic + potential + elastic energy)” is almost always conserved. But let’s think for a moment. External forces, like the normal force (or tension in a rope), are at work on a roller coaster (or pendulum). So, shouldn’t mechanical energy NOT be conserved?

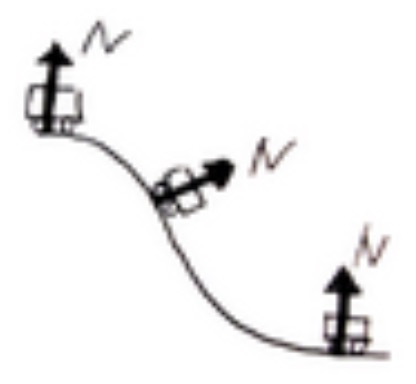
What’s going on here? The secret is that the normal force and tension always act perpendicular to the direction of the object’s motion. The work done by a force perpendicular to the direction of motion is zero, so we only need to consider mechanical energy.

In the case of a roller coaster

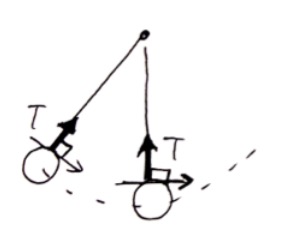
In the case of a pendulum

While it’s difficult to calculate the exact magnitude of the normal force or tension, they do no work in this way. Therefore, no matter what path an object takes, its mechanical energy is conserved (So what kind of effect do the normal force and tension have on this motion?)

Using this principle, you can even calculate the speed of the swing that Heidi from “Heidi, Girl of the Alps” rides. It’s the giant swing from the beginning of the opening credits.

For example, if the swing ropes are 30m long (you can estimate this from the swing’s period) and the angle is 60°, what would the speed be at the lowest point? Heidi might be all smiles, but it turns out she’s on a pretty extreme ride!

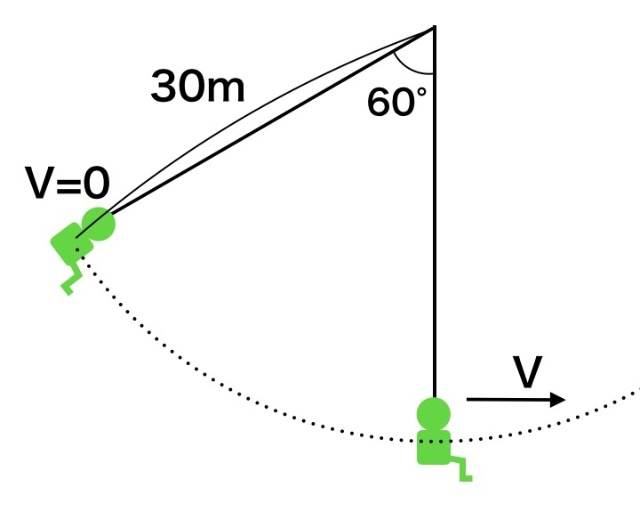
Why don’t you try to calculate it yourself?

Summary

Everyday theme park rides can be explained with knowledge from a textbook—realizing this connection between science and your daily life is the most valuable part of this lesson. Learning isn’t just for the classroom. The theme park can be your classroom, too.

Click Here for Our Online Lessons

#ConservationOfMechanicalEnergy #MechanicalEnergy #Work #DisneylandPhysics

・Conservation of Mechanical Energy (Roller Coaster)

・Conservation of Mechanical Energy (Swing)

Let’s calculate the speed of a roller coaster using the Law of Conservation of Mechanical Energy!

Big Thunder Mountain Problem Form

Heidi’s Swing Problem Form

Mechanical Energy Conservation Slide

Handout (Roller Coaster)

Handout (Swing)

Contact & Requests

Explore the wonders of science up close! We have a collection of fun science experiments you can do at home, with easy-to-understand tips. Feel free to browse around!
・About the Author, Ken Kuwako, click here
・For various requests (writing, lectures, science classes, TV supervision, appearances, etc.), click here
・Article updates are posted on X!

Our Science Fun Channel posts experiment videos!

４月のイチオシ実験！

テレビ番組・科学監修等のお知らせ

  • 4月9日（木）「THE突破ファイル」（日本テレビ ）の科学監修を行いました。夜7時〜となります。

書籍のお知らせ

  • サクセス15 ４月号にて、野球の科学について記事を執筆しました（2026/3）
  • 『大人のための高校物理復習帳』（講談社）…一般向けに日常の物理について公式を元に紐解きました。特設サイトでは実験を多数紹介しています。※増刷がかかり６刷となりました（2026/02/01） スクリーンショット 2014-07-05 0.43.51
  • 『きめる!共通テスト 物理基礎 改訂版』（学研）…　高校物理の参考書です。イラストを多くしてイメージが持てるように描きました。授業についていけない、物理が苦手、そんな生徒におすすめです。特設サイトはこちら。

講師・ショー・研究等のお知らせ

Explore

  • 楽しい実験…お子さんと一緒に夢中になれるイチオシの科学実験を多数紹介しています。また、高校物理の理解を深めるための動画教材も用意しました。
  • 理科の教材… 理科教師をバックアップ！授業の質を高め、準備を効率化するための選りすぐりの教材を紹介しています。
  • Youtube…科学実験等の動画を配信しています。
  • 科学ラジオ …科学トピックをほぼ毎日配信中！AI技術を駆使して作成した「耳で楽しむ科学」をお届けします。
  • 講演 …全国各地で実験講習会・サイエンスショー等を行っています。
  • About …「科学のネタ帳」のコンセプトや、運営者である桑子研のプロフィール・想いをまとめています。
  • お問い合わせ …実験教室のご依頼、執筆・講演の相談、科学監修等はこちらのフォームからお寄せください。
 
Categories
Science
Science

Previous article

Don’t know where θ goes? Clear it up with a drawing trick! (A story connecting nursing and high school physics on “Force Decomposition”)
2025年9月3日
Science

Next article

Measuring Reaction Time with a Ruler: The Ruler Drop Experiment
2025年9月4日