物理が解ける！「３ステップ解法」と「逆算思考」

受験生は必見

パターン解法の通用する問題と

通用しない問題への対応について！

 

パターン解法が有効なとき

ぼくが使っている「３ステップ解法」は

「ぶつりの１・２・３」という本でまとめましたが、

問題の解法を３つのステップにわけて、

順番に実行していくことによって

答えにたどり着けるようになる解き方です。

例えば運動方程式の問題を解くときには、

 

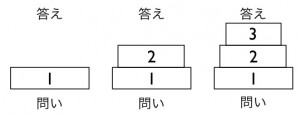
１　絵を描く

２　静止・等速　または　加速　でグループ分け

３　静止・等速→力のつり合い　／　加速→運動方程式

 

というように、わかる生徒ならすぐに作っている運動方程式

について、どのような考えで作っているのかが順序立てて

見えるようにしています。

 

漆原晃先生の書いている「明快解法講座」や橋元先生の橋元流解法の大原則

についても同様のパターン解法での説明が多く見られます。

 

このパターン解法を使うと、物理が苦手な生徒でも

得点できるようになり定期テストで

良い成績を残すことができます。

 

このようなパターン解法は意外に思うかもしれませんが、

MARCH系までの大学の入試問題で効果を発揮します。

 

これで初学者は物理が面白くなります。

つまり、パターン解法形式の問題集をまずは買ってみて、

物理をすきになるのが第一歩ということになります。

 

逆算思考のススメ

ただし上位校の入試問題では「パターン解法」

は簡単には通用しなくなってきます。

 

ここで物理がまた嫌いになってきます。

「受験では結局使えないじゃない・・・。」

 

例えばレールの上をボールがすべって、

レールが円形になっており、

ボールがくるっとすべるような問題。

 

昨日、このような問題に授業中に取り組みました。

この場合、円運動の運動方程式を作って、はい！終わり。

 

ではなくて、その後にボールが面からはなれて落ちたりしてきます。

また等速円運動ではなく、非等速であるのも特徴です。

 

今日授業で扱かった問題には、

ボールが面から離れて落ちるときの最高点の高さを

求めなさいというような問題でした。

 

パターン解法では円運動の運動方程式までで終わってしまい、

その後は問題によって様々に条件が変化していきますから、

ココ止まりとなってしまいます。

 

そんなときに使えるのが、「逆算思考」です。

 

逆算思考は全ての問題で使えます。

 

パターン解法になれすぎてしまうと、

問題を見た瞬間に、例えば運動方程式までは作っていきますが、

さて問題を見ると一見違うものを求めるように

指示されていて、ココでストップです。

 

これはパターン解法が、ボトムアップ方式の考え方によるものだからです。

ある条件が与えられたら、この条件の問題の「定番」は

まずは○○して、○○する。

 

対して「逆算思考」は与えられた問題からスタートします。

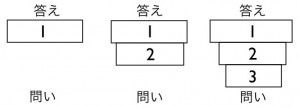
１　問題で問われているものを確認する。

２　問われているものと関係のある式を作る

３　その式を作るために求める必要のあるものをあぶり出す

 

というような流れになります。つまりトップダウンに近い考え方です。

 

例えばさっきの問題であれば、

 

１　問われているものを確認する

問われているものは最高点の高さでした。これが出発点。

 

２　問われているものから作れる式を考える

最高点の高さということは、投げ上げ運動。

離れるときの速度と角度がわかれば、

力学的エネルギーの保存で高さがわかる。

 

３　その式を作るために求める必要のあるものをあぶり出す

速度と角度がわかればいい。離れるときの条件は、垂直抗力が０になるところ。

運動方程式を作って、垂直抗力をゼロにする。

 

速度については、スタート地点と離れるときの力学的エネルギー保存かな？

 

という感じです。

 

逆算思考で問題を解くようにできるようになると、

また物理が面白くなってきます。

 

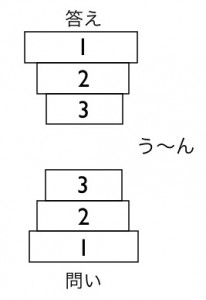
ではパターン解法は捨てたほうがいいのか？というと、

そうでもありません。難しい問題に対応するときには、

１　逆算思考でゴールから考えて見る（トップダウン）

２　まずパターン解法で数式を作ってみる（ボトムアップ）

３　１と２がくっつかないか考える

 

というように、考えることができるためです。

 

このような問題は、もう出題者との戦い。

ゴールにたどり着けるかどうかはわかりませんが、

パターン解法を知っていると選択肢が増えます。

とっても面白くなっているはずだと思います。

 

ではこの逆算思考が学べるのは、何かというと、

たぶん「標準問題精考」などの問題集でひたすらたくさんの問題を

あびるのが一番です。

 

そのさい、友達といっしょに考えたり、わからない生徒に教えたり、

そういった協働学習も有効であると思います。

 

逆算思考をつかうもので面白い問題は、

東工大の問題がおすすめです。

（生徒から質問を受けたとき、

初見で東工大の問題は結構解けないときもあります（汗）

そんなときは宿題にして自宅で考えます。）

 

逆算思考でパターン解法が作れるようになってくる

そしてこの思考法が身につくと、

世の中の見え方も変化してきます。

 

物理に限らず、ある方法について何パターンも

道があることが見えてくるとおもいます。

（または検討をする）

 

そしてパターン解法の参考書の著者が、

なぜこんなパターン別けをして解法を作っているのかにも

思考が及ぶでしょう。

 

ここまで行けば、もう物理を教えられるレベルだと思います。

 

物理を学びながら、いろいろなことが繋がっていく、

応用がきくようになる。

 

ここまで生徒が到達するのを助けていきたいなというのが、

演習での目標です。

 

参考文献

パターン解法で役立つ本・問題集

物理I・II基礎問題精講

手前味噌ですが、パターン解法の習得に

ぶつりの1・2・3 誰でも解ける! セ…

橋元先生のほうがかなりざっくりと学べます。漆原先生のほうは全体的に学べます。

漆原晃の物理物理I・II明快解法講座…

橋元淳一郎の物理橋元流解法の大原…

逆算思考がみにつく問題集

標準といいつつ、難しいです！挫折注意！

物理I・II標準問題精講