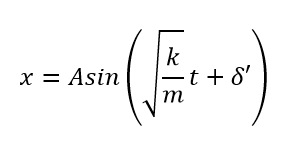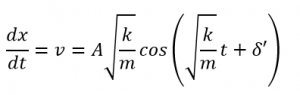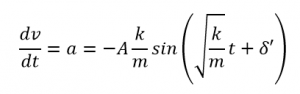微積で求めた数式とイメージを一致させる方法(単振動)
高校物理と微分積分
高校物理の検定教科書では微積を使わないで説明がなされています。数学の進度の関係もあるため、そのようになっていますが微積をつかって考えたほうがスッキリとわかりやすく説明できることも数多くあります。
このコーナーでは微積を使ったほうが良い範囲について、ひとつひとつ説明をしていこうと思います。今回はばねの単振動について考えてみたいと思います。
単振動の数式と物体の振動のイメージ
前回、-定数×変位の力が物体にはたらいていると、単振動をすることを微積によって求めました。
※δ’は積分定数で初期位相を示す
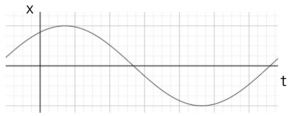
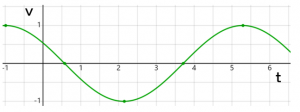
この様子をグラフで示すと次のようになります。横軸が時間軸で、時間とともに振動している様子がよくわかりますね。
前回は、宿題としてこの変位をもう一度微分をして、速度、さらに微分をして加速度を出してみましょう!というものを出しましたが、今回はその答え合わせをやってみたいと思います。
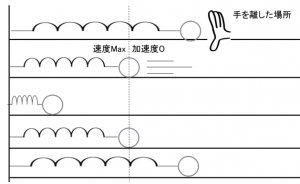
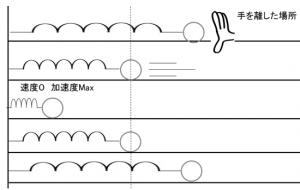
まずは、振動の様子から見ていましょう。
例えば単振動をはじめた物体は、原点で速度が最大になりますが、このときバネは伸びていないので、加速度はというと0になります。
それでは実際に上の式を微分して速度や加速度の式を導き、これらのことが表されているのかを見てみましょう。まずは一回微分をして速度を求めます。
これをグラフにすると、次のようになりますね。速度も時間とともに変化していることがわかります。
もう一度微分をして加速度を求めると、
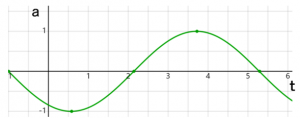
となります。これをグラフにすると、次のようになります。
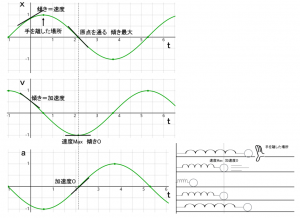
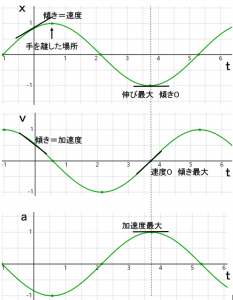
加速度も時間とともに変動していることがわかりますね。それではx、v,a、の3つのグラフを並べてみてみましょう。
x-tグラフの傾きは速度を、v-tグラフの傾きは加速度を示します。ここでボールが振動の中心を通るときの時間を見てみましょう(図の中の破線で示した部分)。原点を通るとき、x座標は0となります。このとき速度は負の向きに最大になり、そして加速度は0となっているのがわかりますね。上の単振動の様子を見た図と同じことが示されました。
もうひとつ確かめてみましょう。例えばこの場所、
ばねがもっとも縮んだ時です。ばねの縮みは最大になっており、折り返し地点となりますから、一瞬物体は静止しているので0、またばねはもっとも縮んでいるので力が最大、つまり加速度は最大になっています。
先ほどと同じように3つのグラフを並べて、最も縮んだときの時間を見ていくと、
図の点線の部分を見てください。確かに単振動の様子と一致をしていることがわかりますね。
このように、微積を使って求めた変位、そしてそれぞれの時間の速度や加速度が、実際の現象と一致をしていることがわかります。面白いですよね(^^)。
ただ実際の高校入試では、これらの極端なとき(例えば振動中心や両端など)のみ聞かれ、基本的には、この間の場所については聞かれません。
ニュースレター
・ニュースレターはブログでは載せられない情報を配信しています。
[subscribe2]