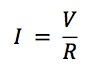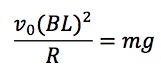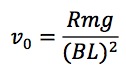なぜ導体棒にはブレーキがかかるの?コの字型回路(抵抗パターン)
今日は生徒から受けた質問についてお答えします。よくある問題なのですが、コの形をした回路においた導体棒ついてです。なぜ導体棒を動かしていくと、最終的にブレーキがかかるのか?ということがわからないようでした。似たもんだいを新たに作問しましたので、この問題を通して、みなさんと考えていきたいと思います。なお電池がついている問題パターンはこちらを御覧ください。
問題
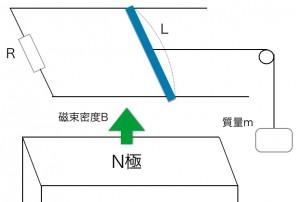
図のように上向きの磁束密度Bが貫く空間の中に、カタカナの「コ」の形をした導線を水平にして置いた。この導線には抵抗Rがついている。この導線の上に質量の無視できる軽い導体棒(長さL)をおいて、質量mのおもりで引っ張った。次の各問に答えなさい。ただし、重力加速度はgとする。
(1) 導体棒の速度がある速さvになったときの、誘導起電力の大きさと向きを求めなさい。
(2) 回路に流れる電流の大きさを求めなさい。
(3) 棒にはたらく電流が磁場から受ける力の大きさと向きを求めなさい。
(4) 時間が十分経過すると、導体棒は一定の速さで移動をした。このときの速さv0を求めなさい。
解答・解説
まずはチェック!
さてみなさんはわかりますか?
この問題はローレンツ力(ミクロ)と、電流が磁場から受ける力(マクロ)を
それぞれ考えていく問題なので、少し難しいと思います。
ポイントは、最終的には導体棒にはたらく電流が磁場から受ける力と、おもりが棒を引く力がつり合うということです。
まず全体としてどのようなことが起こるのかを確認しましょう。
実はこの問題、次のようなことが起こるんです。
1 棒が電池になる
2 電流が流れる
3 ブレーキがかかる
それぞれについて見ていきましょう。
<1 棒が電池になる>
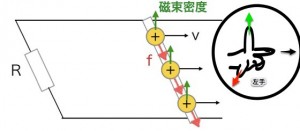
導体棒の中にあるプラスの電荷を考えてみてください。
棒が右に動くということは、これらの電荷も右に動いているということになります。
これらの電荷はローレンツ力(ミクロな電磁気力)によって、図の手前側に力を受けます。
(なお実際は自由電子が動いているのですが、今回はわかりやすくするためにプラスの電荷の動きを考えています)
右に動いている棒は、プラスの電荷を手前に動かそうとしています。
電荷を動かそうとする能力、これが電圧ですね。
つまり棒は手前がプラスの電池になっています。
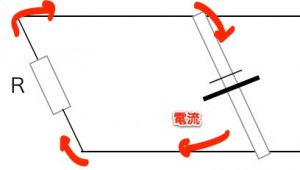
<2 電流が流れる>
棒が電池になったことによって、電流が流れます。
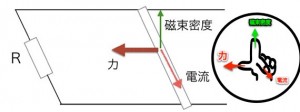
<3 ブレーキがかかる>
ここが難しいところですが、このことにより導体棒にはブレーキがかかるんです。
必ず棒の動きを止めようとする向きにはたらくことがポイント。
というのも、流れた電流によって、直線電流が磁場から力を受けるからです(マクロな電磁気力)。
これはこの回路をコイルとみると、コイルを貫く磁場が増えてしまうため、
ブレーキがかかるというように見てしまってもかまいません。
棒が左側に動いたとしても、どうようにブレーキがかかる、右向きの力がはたらきます。
このような問題は、電池、電流、ブレーキとおぼえておきましょう。
良いでしょうか。
電池、電流、ブレーキ!
です。
それでは問題を解いてみましょう。
(1) 導体棒がある速度vになったときの誘導起電力の大きさは、公式を使えば一発ですね。V = BLVです。向きは手前の方向がプラスですね。
(2) 回路に流れる電流は、
オームの法則から、V = IR(オームの法則)を電流について解くと、誘導起電力を代入すると、
となります。
(3) 導体棒にはたらくブレーキの力を求めます。
電流が磁場から受ける力の公式より、
F = LIB
ここに、電流の大きさを代入すると、
となります。
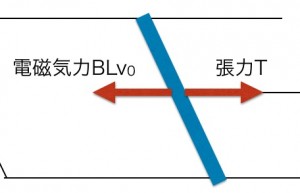
(4) 速度が一定になったときの速さをv0とおくと、等速度運動なので、このとき棒にはたらく力は張力Tとつり合っているはずです。
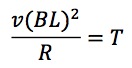
(左向きの力=右向きの力)
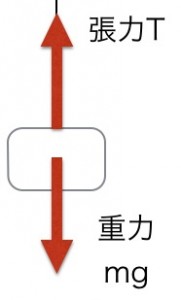
またおもりも同様に等速度運動をしているので、上下方向の力のつりあいから
T = mg
(上向きの力=下向きの力)
となります。2つの式からTを消去すると、
これをv0について解くと、
となります。
ニュースレター
・ニュースレターはブログでは載せられない情報を配信しています。
[subscribe2]